julesx

Bonsoir, Et toi, pendant ce temps, tu fais quoi, tu joues à tes jeux préférés sur ton smartphone ?

Bonsoir, Regarde sur Internet ce qui se dit à propos de la résolution des équations diophantiennes. Tu trouveras en particulier comment on obtient la solution générale qui te pose problème.

Je vois mal comment il pourrait en être autrement. Et que devient p(A U B) si c'est bien le cas ? Dans ce cas, on a p(A U B) = p(A) + p(B) et comme les probabilités sont forcément positives ou nulles, chacune des deux est inférieure ou égale à p(A U B).

.

Normalement, a priori c'est p(A U B) = p(A) + p(B) - p(A ∩ B) sauf si A et B sont indépendants. Est-ce le cas ici ?

On a Partant de là, * soit tu laisses tel quel * soit tu mets 10 en facteur * soit tu réduis au même dénominateur.

Bonjour, Au cas où personne ne te répondrait, à la louche, moi je dirais que la probabilité de l'union (M500≥0,4)U(M500≤-0,4) est forcément supérieur ou égal à la probabilité de chacun des deux termes pris isolément, donc p(M500≥0,4)≤p(|M500|≤0,4).

Je pense que c'est la meilleure solution. Sur ce site, on est quelques-un à bidouiller avec Python (ou avec d'autres logiciels de programmation) mais je n'ai, jusqu'à présent, pas vu de réponses d'intervenants vraiment au top (mais je ne suis pas là depuis le début). Si je me trompe, qu'ils se manifestent ! La difficulté est aussi d'adapter la démarche de la programmation à celle du concept mathématique que l'on veut étudier. Bon courage !

Bonsoir PAVE, Juste une rectification, c'est P(x<=k), ! Ma calculette (TI 85) non plus ne comporte pas cette fonction, mais elle a le mérite de toujours fonctionner à 100%, d'avoir une fonctionnalité de touches programmables et quelques facilités pour d'autres options que je n'ai pas retrouvé ailleurs.

Bonjour, Les enseignants de maths confirmeront ou infirmeront, mais il me semble qu'a priori, l'étude part de p(X<=k), donc les concepteur de calculettes ont dû considérer qu'il était inutile de rajouter la possibilité p(X>k) puisque la somme des deux fait 1. Cela dit, j'ai vu que Numworks offre les deux, enfin pas tout à fait, les options sont p(X<=k) et p(X>=k). Pour éviter aux élèves d'avoir à passer par p(X>k)=1-p(X<=k-1) ?

Bonjour, J'ai essayé ton script, en rajoutant ce qu'il faut pour pouvoir l'exécuter et afficher la courbe. Dans le def heun, j'ai du mettre return t,y mais c'est annexe. A priori, je ne vois donc pas d'erreur. Par contre, comme je n'ai pas étudié de près les différentes méthodes, je ne sais pas laquelle doit donner les meilleurs résultats. Je sais juste qu'en principe, on recommande RK4. Bon, si on augmente suffisamment la valeur de N, on finit par rendre indiscernable les courbes obtenues avec heun et la courbe théorique, mais je ne pense pas que cela résolve ton problème. Essaie de voir sur la toile, il y a peut-être des forums qui traitent de cela.

Merci de poster les images dans le bon sens, ceux qui travaillent avec un PC de bureau t'en sauront gré. 2) Non, car F(0)=5 et ta primitive donne F(0)=0. Revois la notion de primitive.

Bonjour, Attention, je n'ai pas tout compris, mais voilà un script que marche, que j'ai trouvé sur Internet. from scipy.optimize import fsolve import numpy as np import matplotlib.pyplot as plt def f(y, t): return np.sin(t)*np.cos(y) def euler_implicite(f,a,b,y0,n): t,Y,h=[a],[y0],(b-a)/n for i in range(1,n+1): t.append(i*h) Y.append(fsolve(lambda y:Y[i-1]+h*f(t[i],y)-y,0.01)) return t,Y t,Y=euler_implicite(f,0,100,1,1000) plt.plot(t,Y) plt.show() La seule chose que je constate par rapport au tien, c'est qu'on fait la différence entre la liste Y et le y qui apparaît dans une partie du "def". Mais pour le reste... A toi de voir si tu peux en tirer quelque chose

Ce qu'on cherche, ce sont les ordonnées des points C et D, cf. pièce jointe ci-dessous.

Donc,puisque c'est (0,2) tu as la réponse, non ?

Je ne comprends pas bien ton problème. D'après ce qu'a dit ton professeur, soit * il ne veut pas d'un coefficient décimal * il a compté en termes de carreaux.

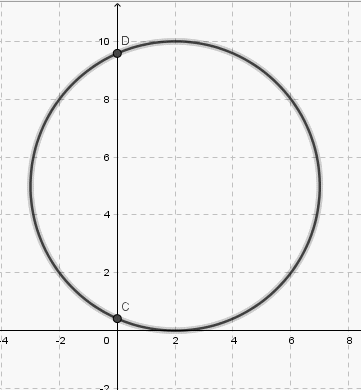
Oui, dans l'équation du cercle x²+y²-4x-10y=-4. Tu obtiens ainsi une équation en y dont il suffit de chercher les solutions.

Bonjour, S'il y a encore des problèmes, n'hésite pas à revenir sur ce fil.

Bonjour, La démarche est la même, sauf que les "pas" font 0,5 et que tu vas vers la gauche. A partir de A, tu vas vers la gauche de 2 pas, donc en abscisse, c'est -1, tu montes de 5 pas, donc en ordonnée c'est 2,5. La pente est donc de 2,5/(-1)=-2,5. Tu aurais aussi pu partir de B, donc avancer de 1 et descendre de 2,5, ce qui donne -2,5/1=-2,5 pour la pente.

Dans ton cours, il est dit que, dans l'équation cartésienne d'une droite ax+by+c=0, a et b sont les coordonnées d'un vecteur normal à la droite. Donc, comme le vecteur AB est un vecteur normal de la tangente, tu sais déjà que son équation est de la forme 3x+4y+c=0. Il ne reste plus qu'à utiliser le fait qu'elle passe par le point B pour trouver la valeur de c.

Je viens de voir la rectification dans ta réponse, il vaut d'ailleurs mieux reposter un nouveau message, car une ré-édition n'apparait pas dans l'historique, donc on passe à tout les coups à côté. 2**0,5 signifie 2 à la puissance 0,5, soit 2 à la puissance 1/2 qui est la même chose que racine(2). J'ai utilisé ce procédé car, pour employer sqrt(2), il aurait fallu importer le module maths. Mais rien ne t'empêche de le faire.

C'est le signe de la dérivée qui permet de conclure sur les variations de la fonction, cf. cours. Il faut donc chercher le signe de la dérivée sachant que m est négatif et peut varier entre -∞ et 0.

Tu sais que la tangente est perpendiculaire au rayon, donc à la droite (AB). Partant de là, * soit tu raisonnes en termes de coefficients directeurs * soit tu raisonnes en termes de vecteur normal dans les deux cas, tu termines en utilisant le fait que le tangente passe par le point B(5;9).

C'est ça, tu peux passer à l'autre exercice.

Bonjour, Juste une alternative à la question 4 : Utiliser le fait que le vecteur AB est un vecteur normal de la tangente.