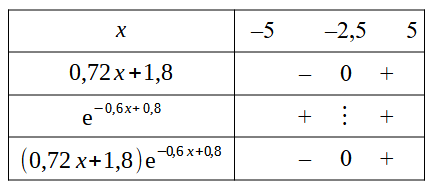julesx

Re-bonjour, Je ne sais pas si ça va pouvoir te servir. J'ai trouvé ça sur la toile à l'adresse https://fr.mathworks.com/matlabcentral/answers/360751-solving-lorenz-attractor-equations-using-runge-kutta-rk4-method clc; clear all; t(1)=0; %initializing x,y,z,t x(1)=1; y(1)=1; z(1)=1; sigma=10; %value of constants rho=28; beta=(8.0/3.0); h=0.01; %step size t=0:h:20; f=@(t,x,y,z) sigma*(y-x); %ode g=@(t,x,y,z) x*rho-x.*z-y; p=@(t,x,y,z) x.*y-beta*z; for i=1:(length(t)-1) %loop k1=f(t(i),x(i),y(i),z(i)); l1=g(t(i),x(i),y(i),z(i)); m1=p(t(i),x(i),y(i),z(i)); k2=f(t(i)+h/2,(x(i)+0.5*k1*h),(y(i)+(0.5*l1*h)),(z(i)+(0.5*m1*h))); l2=g(t(i)+h/2,(x(i)+0.5*k1*h),(y(i)+(0.5*l1*h)),(z(i)+(0.5*m1*h))); m2=p(t(i)+h/2,(x(i)+0.5*k1*h),(y(i)+(0.5*l1*h)),(z(i)+(0.5*m1*h))); k3=f(t(i)+h/2,(x(i)+0.5*k2*h),(y(i)+(0.5*l2*h)),(z(i)+(0.5*m2*h))); l3=g(t(i)+h/2,(x(i)+0.5*k2*h),(y(i)+(0.5*l2*h)),(z(i)+(0.5*m2*h))); m3=p(t(i)+h/2,(x(i)+0.5*k2*h),(y(i)+(0.5*l2*h)),(z(i)+(0.5*m2*h))); k4=f(t(i)+h,(x(i)+k3*h),(y(i)+l3*h),(z(i)+m3*h)); l4=g(t(i)+h,(x(i)+k3*h),(y(i)+l3*h),(z(i)+m3*h)); m4=p(t(i)+h,(x(i)+k3*h),(y(i)+l3*h),(z(i)+m3*h)); x(i+1) = x(i) + h*(k1 +2*k2 +2*k3 +k4)/6; %final equations y(i+1) = y(i) + h*(l1 +2*l2 +2*l3 +l4)/6; z(i+1) = z(i) + h*(m1+2*m2 +2*m3 +m4)/6; end plot3(x,y,z) C'est du Matlab, ça devrait pouvoir se transcrire. Il n'y a que les lignes f=@(t,x,y,z) sigma*(y-x); %ode g=@(t,x,y,z) x*rho-x.*z-y; p=@(t,x,y,z) x.*y-beta*z; qui sont à "décoder", mais ça correspond peut-être à la notion de def de Python. Mais ne m'en demande pas plus, je n'ai jamais utilisé Matlab autrement qu'avec la sous-couche Simulink.

Bonjour, C'est de trouver la valeur à p près telle que cos(x)=x (en d'autres termes, de résoudre numériquement l'équation f(x)=0).

De rien, bonne continuation.

Bonsoir, Ton post en maths a été verrouillé, mais c'est accessoire. Par contre, à mon avis, pour que tu aies une aide, je pense qu'il faudrait que tu réduises ton script à la seule partie qui pose problème. Si c'est possible évidemment, je ne suis pas assez compétent dans ce domaine pour en juger.

Bonjour, Un exemple de base possible est celui consistant à transformer une image en couleur en image en niveaux de gris, cf. script ci-dessous from PIL import Image img = Image.open("essai.png") img = img.convert('L') img.show() Attention, comme dit dans l 'énoncé, il faut que le fichier image (essai.png ici) soit dans le dossier courant. Pour les autres possibilités du module, regarde par exemple le site ci-dessous. https://info.blaisepascal.fr/pillow Si nécessaire, je te joins un fichier png.

De rien, bonne continuation.

Re-bonjour, OK pour le début. A la rigueur, j'aurais écrit un=430*e0,14*n. Pour le taux d'évolution tu aurais pu trouver très rapidement l'expression sur Internet. On a : taux d'évolution en % =(un+1-un)/un*100 soit, après simplification par un, (e0,14-1)*100. Pour l'algorithme, moi, je trouve n=16. Pour n=15, on n'a que 3511 abonnés Ta justification pour la suite vn n'est pas correcte. vn=12*un => vn+1=12*un+1=12*un*e0,14=12*vn C'est cela qui justifie que la suite vn est géométrique de raison 12 et de premier terme 5160. Tu revois la fin, c'est la somme des termes d'une suite géométrique. Voir cours.

Petits compléments : Dans ce qui précède, je n'ai envisagé que les cas strictement supérieur ou strictement inférieur. Si N est égal au nombre le plus grand de la partie gauche, il est inutile d'aller plus loin, ce nombre est évidemment bien présent. Ceci réduit éventuellement le nombre de sous-tableaux à envisager. A titre d'exemple, pour N=10, on a, dès la première séparation, l'égalité avec le terme maximum de [0;2;4;6;8;10], donc la recherche s'arrête là. Un exemple d'algorithme utilisant un démarche légèrement différente est donné ici https://fr.wikipedia.org/wiki/Recherche_dichotomique#Écriture_itérative

Bonjour et bienvenue sur le site, Ci-joint le script, attention aux indentations si tu le transcris dans ton logiciel Python. Egalement, suivant celui que tu utilises, il faudra rajouter éventuellement des print avant les convertir ([1, 0, 1, 0, 0, 1, 1]) et convertir ([1, 0, 0, 0, 0, 0, 1, 0]). La structure est classique sauf que, comme les termes de T se lisent de gauche à droite, il faut "inverser" les puissances de 2, d'où le 2**(L-i-1) def convertir(T): S=0 L=len(T) for i in range(L): S=S+2**(L-i-1)*T[i] return S

De rien, bonne continuation.

C'est ça.

Bonsoir, Si le tableau est trié, ce qui est le cas, une approche possible : Tu divises le tableau en 2 parties, gauche et droite. Si le tableau contient un nombre impair d'éléments tu prends pour celui de gauche le plus petit des deux. Si le nombre N dont tu cherches la présence et supérieur au nombre le plus grand de la partie gauche, tu conserves la partie droite, sinon tu conserves la partie gauche. Avec la partie conservée, tu recommences la démarche précédente. Tu fais cela jusqu'à ce que la partie conservée ne comporte plus qu'un seul terme. Dans ce cas, deux possibilités: * Le terme est égal au nombre recherché, dans ce cas, il y a présence du terme N dans la liste. * Il n'y a pas égalité, N ne fait pas partie de la liste. Exemples avec tes données : TAB = [0;2;4;6;8;10;12;14;16;18;20;22] Les deux parties sont [0;2;4;6;8;10] et [12;14;16;18;20;22] 11 est supérieur à 10, donc on conserve [12;14;16;18;20;22] Les deux parties sont [12;14;16] et [18;20;22] 11 n'est pas supérieur à 16 donc on conserve [12;14;16] Les deux parties sont [12] et [20;22] 11 n'est pas supérieur à 12 donc on conserve [12] Comme il ne reste qu'un terme et qui est différent de 11, 11 ne fait pas partie de la liste. TAB = [0;2;4;6;8;10;12;14;16;18;20;22] Les deux parties sont [0;2;4;6;8;10] et [12;14;16;18;20;22] 20 est supérieur à 10, donc on conserve [12;14;16;18;20;22] Les deux parties sont [12;14;16] et [18;20;22] 20 est supérieur à 16 donc on conserve [18;20;22] Les deux parties sont [18] et [20;22] 20 est supérieur à 18 donc on conserve [20,22] Les deux parties sont [20] et [22] 20 n'est pas supérieur à 20 donc on conserve [20) Comme il ne reste qu'un terme et qui est égal à 20, 20 fait partie de la liste. Ceci te permet en particulier d'identifier les sous-tableaux. Pour l'algorithme, essaie de voir ce que cela peut donner. Bon courage...

Encore la même erreur de calcul ! -1,2x-5=0 => x=-5/1,2=-4,1667... que tu peux éventuellment arrondir à -4,2. En plus, tes signes de f(x) sont faux, f(x) est positif entre-5 et -4,2 et négatif ensuite. Donc, g(x) croit entre -5 et -4,2 (environ) puis décroit ensuite. Il s'ensuit que la bonne courbe est la numéro ....

Bonjour, Mais tu n'as pas complété ton tableau de signe ! Le premier terme est négatif entre -5 et -2,5 puis positif après. L'exponentielle est toujours positive. Le produit des deux s'en déduit, cf pièce jointe ci-dessous. Tu rajoutes une ligne pour les variations de f(x) : Vu le signe de f'(x), f(x) est décroissante entre -5 et -2,5 puis croissante ensuite .On retrouve les éléments de la courbe donnée dans la partie A. N.B. : Je viens de m'apercevoir que tu as fait une erreur de calcul : x=1,8/(-0,72)=-2,5.

Bonjour, Je ne comprends pas trop ce qui t'arrête dans la question 1. En fait, on te demande la nature de la surface de séparation entre la calotte sphérique et le cylindre. C'est tout simplement le disque de centre O1 et de rayon O1A=3,6 cm, donc, en particulier, la surface supérieure du cylindre.

Bonjour, Quelques rectifications... f(3) est bien égal à -8,6/e, mais tu as oublié le signe - dans le calcul approché. Pour f'(3), j'aurais plutôt donné le résultat "exact" sous la forme 11,88/(3e). Il y a une erreur dans ton équation de la tangenta à cause du signe oublié pour f(3), la bonne équation est : y=1,46x-7,54 (-4,38-3,16) Pour la dernière question, je suppose que c'est celle du A ? Pour le moment, tu ne connais pas l'équation de la dérivée, par contre, tu vois sur la courbe fournie qu'il y a une tangente parallèle à l'axe des abscisses, ce dont tu déduis que la dérivée est nulle en ce point. Donc α est l'abscisse du point D, soit -2,5. Tu passes aux parties suivantes ?

Bonjour PAVE, Merci pour les infos à propos des animations. Avant de t'en parler, j'avais effectivement essayer de passer par la création de gif animé, mais vu le temps que ça a mis et la taille du fichier final, je me suis dit qu'il y avait peut-être une autre solution. Donc, vu ta réponse, c'est bien la seule possibilité. Je ré-essaierai à l'occasion avec les modifications que tu suggères. A propos du fichier récalcitrant, j'ai bien réussi à l'ouvrir (comme tous ceux que tu postes) y compris directement à partir de la citation dans le post de l'élève. Donc le problème se situe ailleurs. Bonne après-midi.

Bonsoir PAVE, A propos de l'ouverture impossible, peut-être une histoire de version ? Il faudrait que Ffpp donne celle qu'elle utilise. En passant, petite question, quelle est la démarche pour joindre des fichiers animés dans les posts ? Je sais les animer sous Geogebra mais, a priori, je ne sais sauvegarder que des images fixes. On passe par un gif animé ? A propos, je me suis aperçu l'option "alterné" de "Répété" fonctionne très bien avec des curseurs, par contre, j'avais essayé un truc analogue avec un point circulant sur une courbe délimitée, et là, ça devient beaucoup plus aléatoire. Arrivé au bout, ça met un temps plus ou moins long avant de faire demi-tour. Bonne soirée.

Bonjour, La partie A ne pose pas de problème. f(3) est l'ordonnée du point A. f'(3) est le coefficient directeur de la droite (AB) dont on connait le coordonnées des points A et B. La relation donnant l'équation de la tangente est dans ton cours. Il suffit d'annuler cette relation pour obtenir la valeur de α. Poste les résultats que tu obtiens pour cette partie et on verra pour la suite.

Non, "projeté orthogonal de D sur le cercle" ne veut rien dire. Par contre, ce que tu peux dire, c'est que le triangle ADE est rectangle en D, car AE est un diamètre du cercle et D un point du cercle. Il s'ensuit que D est le projeté orthogonal de E sur la droite (AD).

OK, si nécessaire, continue sur ce fil.

Bonjour, Je ne suis qu'un amateur, j'ai fouillé un peu la toile pour trouver ceci : * Pour l'endomorphisme, il faut calculer An qui est égal à P.Dn*P-1 avec Dn= (1 0 0 2n) * Pour le calcul des intégrales, au moins les 3 premières sont développées ici http://www.bibmath.net/ressources/index.php?action=affiche&quoi=bde/analyse/integration/integrales-multiples&type=fexo

Tu continues ici ou sur ton autre fil ? Ce fil n'existant plus, il faut continuer ici. Je répète ma question : Tu connais l'inégalité de Bienaymé-Tchebychev ? Sinon, cherche son expression sur la toile.

Bonjour, Tu aurais du poster chaque exercice séparément vu qu'ils correspondent à des éléments de programme très différents. Pour l'exercice 2 : 1) Tu as dans ton cours la solution de l'équation différentielle y'(x)=ay(x)+b. Il suffit de la transposer en remplaçant x par q et y par P. 2) Inutile de passer par la dérivée. Sur l'intervalle [0;14], e-0,4q est décroissante, donc 1+15e-0,4q est décroissante et son inverse est croissante. 3)a) La droite (OQ) passe per les points O(0,0) et Q(q,f(q)) donc son coefficient directeur vaut [f(q)-0]/(q-0)=f(q)/q. b) Le coût moyen est minimum lorsque le coefficient directeur de (OQ) l'est. Regarde comme évolue ce coefficient directeur lorsque tu déplaces Q sur le tracé fourni. N.B.: Pour le premier exercice, je n'y connais pas grand chose mais ne devrait-on pas avoir E(Z)=6*E(X) et V(Z)=6²*V(X) ? Et pour la question 2, tu connais l'inégalite de Bienaymé-Tchebychev ? Sinon, cherche son expression sur la toile.

Tu crois vraiment que ça va faire avancer le schmilblick ?