PAVE

Bonjour (c'est le minimum de politesse ☹️ !) Ensuite, "on" n'est pas d'accord pour faire TON travail. Dis nous ce que tu as déjà fait (même si tu penses que c'est faux) et nous t'aiderons à avancer et à progresser. Pour la question a), le point F est le milieu du segment [AB]. Fais une figure. Marque dessus les longueurs connues. A l'école primaire tu as du apprendre à calculer l'aire d'un triangle (ici rectangle, ce qui simplifie encore), alors applique la formule.... puis montre nous ce que tu as fait.😃

Bonsoir Maximus, Il serait bien que tu mettes à jour ton profil puisque tu n'es plus en... sixième 😉.

Bonjour, Je suppose que tu as déjà quelques notions du langage python. J'espère que tu as python d'installé sur ton ordinateur et que tu peux tester le script qui t'est donné (mais ce n'est pas indispensable....). Si oui est ce que ton script "tourne" sans erreur . input() tu connais ?

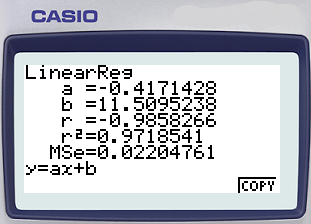
@Paul45 Psitt !! Juste pour te permettre de vérifier tes fastidieux calculs (tes formules sont exactes et tes résultats aussi si on les compare à ceux donnés par Jules),... tu as sûrement une calculatrice qui maitrise fort bien la détermination de la droite d'ajustement affine d'un nuage de points..... tu saisis les couples (xi, yi), tu tapes dans tes mains 😁 et les valeurs de a et b s'affichent 😃 ! C'est un préalable à la recherche des droites de régression.... elles passent (donc toutes !!) par le point moyen (voir le cours, si les formules ne sont pas admises). Il existent pour les calculs "à la main" des formules (dites de Koenig) bien plus pratiques à mettre en œuvre que celles que tu as utilisées. Bon Noël.

Bonjour, C'est vrai que le plus "amusant" avec Scratch, c'est d'expérimenter... Mais cet exercice est faisable sans ordinateur ou autre objet connecté... Si tu regardes bien les 3 scripts, ils ne diffèrent que d'une ligne : celle qui est entre les 2 boucles ! La première boucle trace le triangle et la seconde le quadrilatère. Dans la partie 1, triangles et quadrilatères sont IDENTIQUES d'une figure à l'autre.... Qu'as tu répondu aux questions 1 a et 1 b ? Pour la question 1 c, prends une feuille de papier et un crayon, et pas à pas (ligne après ligne) tu réalises ce que dit le script..... et dis nous ce que tu as trouvé. On te donnera notre avis. A toi.

Jules, nul ne conteste ce que tu dis. Attendons de voir quels sont les besoins de @Dtm110

ou avec une TI...

Hum ! Je me sens tout petit face à une UE finance....😟. Ce qui me gêne le plus, c'est le signe égal et le 0 qui suit.... donc l'aspect équation. Sinon le premier membre exprime la valeur actualisée à l'instant "initial" de trois versements (2120, 2500 et 2970) effectués à la fin des années 1, 2 et 3, en FONCTION du taux t d'actualisation. Tu peux bien sûr saisir cette fonction dans une calculatrice (mode GRAPH) et obtenir (en mode TABle) les valeurs de cette fonction en fonction de la variable qui est le taux d'actualisation. Exemple : si tu prends comme taux d'actualisation 5% (=0,05), la fonction te donnera C0(t) = C0(0,05 ) = ??? Je vais essayer de faire avec ma vieille..... Casio (hélas nul n'est parfait 😇) Si tu regardes pour t= 0,06, tu obtiens un encadrement et en changeant le pas pour les valeurs de t (ou x), tu peux faire une interpolation linéaire (affine). Si tu as compris le principe, essaye de ton coté car afficher les valeurs d'une fonction est le B.A.BA de l'utilisation de ta calculatrice. A suivre.

@Dtm110 S'il te plait, viens vite nous dire ce que tu cherches vraiment dans ta Terminale 😟. Si c'est un taux d'intérêt, j'ai du mal à l'imaginer... imaginaire 😯. Help !

Bonjour, Je suppose que cette équation est l'aboutissement d'un calcul que tu ne nous as pas donné ! Maths financières ? Problème d'actualisation ?? Il serait bien que nous puissions savoir d'où sort cette équation (en bref, donne nous l'énoncé complet !). En l'état de nos connaissances du problème, chaque terme du premier membre est un QUOTIENT (exposant négatifs). On réduit au même dénominateur 0, on multiplie chaque terme de l'équation par (1+t)³ ; on peut poser (1+t) = X . On se retrouve avec une équation polynomiale d'inconnue X... et on résout une modeste équation du second degré qui sauf erreur de ma part n'a pas de solution ! Dis nous tout...

Si ton prof t'a donné cet exercice, c'est qu'il a défini dans son cours ce qu'est un "coefficient multiplicateur". Peut-être même qu'il a démontré la relation entre taux d'évolution (ou de variation) et ce fameux CM. Valeur finale = valeur initiale + ( taux_de_variation x valeur initiale) (cette relation est vue.... en primaire) = valeur initiale [ 1+ taux_de_variation] = valeur initiale * CM CM= 1+taux_de_variation Le CM est le nombre par lequel il faut multiplier la valeur initiale pour obtenir la valeur finale. Si l'évolution est une BAISSE (cad la valeur DIMINUE), alors le taux_de_variation est négatif (-12% = -0,12) et le CM est inférieur à 1 (CM = 1- 0,12 = 0,88) Si l'évolution est une HAUSSE (cad la valeur AUGMENTE), alors le taux_de_variation est positif (+15% = +0,15) et le CM est supérieur à 1 (CM = 1+0,15 =1,15) Regarde ton cours pour avoir des exemples ; refais les exercices....

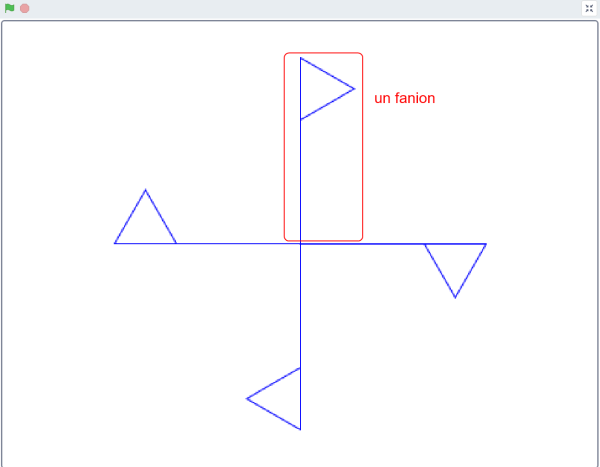
Bonjour, Si on regarde bien la figure à reproduire, il y a un motif (appelons cela un fanion) que l'on fait tourner de 90° autour du point central de la figure. On obtient ainsi 4 fanions. Je suppose que tu disposes du logiciel SCRATCH. Donc tu essaies.... Essaye de faire le script qui dessine le fanion (celui que tu veux : vertical, horizontal ou autre....) Montre nous ce que tu obtiens (même si la figure obtenue n'est pas exactement celle attendue 😟. Pour cela tu peux soit faire une copie d'écran (tu sais faire ?) ou bien mieux tu mets en pièce jointe de ta réponse, le fichier SCRATCH que tu as sauvegardé (tu sais faire ?). A toi d'agir si tu as encore besoin de notre aide

Silence abyssal....

Bonsoir, Tu dois bien avoir un petit bout de cours et quelques exemples. Qu'est ce qu'il dit ton cours ? On veut bien t'aider mais pas question de faire à ta place. Même sans filet (le filet c'est la connaissance du cours), essaye et dis nous... On verra bien où cela coince. A toi de dire.

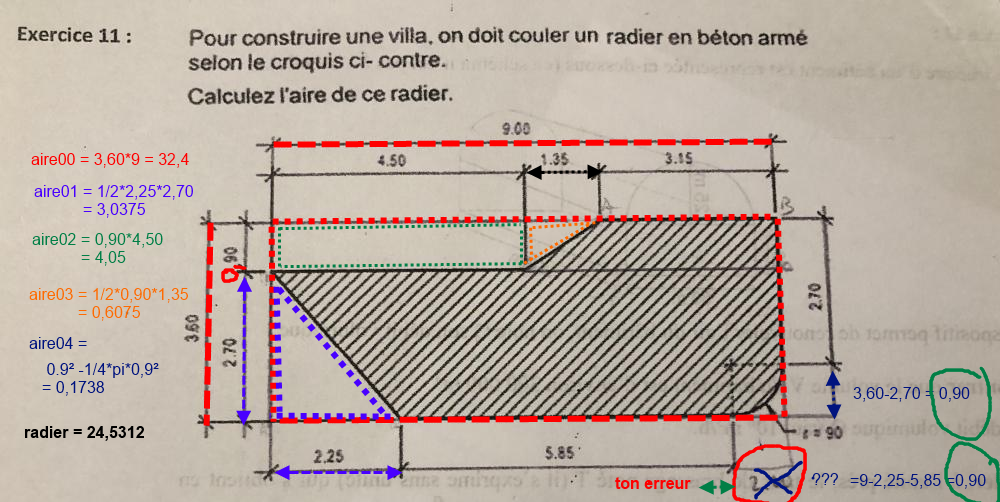
Bonsoir, Si tu connais GEOGEBRA, tu peux VERIFIER tes réponses.... si tu veux 🧐 .EB211207 échelle.ggb

@Black Jack Belles figures ! Avec quels outils es tu parvenu à compléter la figure initiale ?

Bonjour, En complément de la réponse de Jules pour le premier exercice...

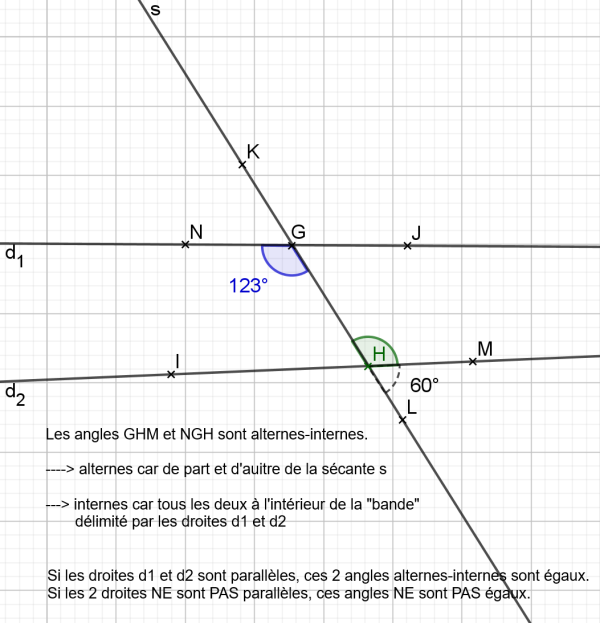
Doublement désolé ! 1) J'étais indisponible cet après-midi. 2) Tu as raison de me signaler l'erreur que j'ai commise.... je me suis basé sur ton affirmation que ce qui est faux (c'est l'angle MHL qui mesure 30°). Si tu te reportes à ma figure https://www.e-bahut.com/topic/58293-geometrie/ il est sans ambiguïté que les angles GHM (120°) et NGH (123°) sont * alternes-internes * et n'ont la même mesure (pas égaux). Es-tu d'accord ?

Effectivement les 2 droites d1 et d2 ne sont pas parallèles mais la raison que tu invoques n'est pas correcte. GHM et NGH ne sont ni correspondants, ni alternes-internes . L'angle NGH (60° d'après l'énoncé) sert uniquement à démontrer que l'angle GHM mesure 120°. On constate alors que les angles alternes-internes GHM (120°) et NGH (123°) ne sont pas égaux donc on en déduit que les droites d1 et d2 ne sont pas parallèles. On peut faire le même raisonnement avec les angles correspondants NGH et IHL. Pense à bien mettre des chapeaux sur les angles quand tu rédigeras sur papier... ici c'est un peu trop compliqué

NON Ils ont le même sommet H donc ils ne peuvent pas être alternes-internes... Ici ils sont tout simplement ... opposés par le sommet. Si on considère l'angle GHM, il a comme alterne-interne un angle de sommet G soit ici l'angle NGH.

Suite Lis d'abord et comprends mon précédent message....

NON Lis attentivement ce que j'ai écrit sur la figure....