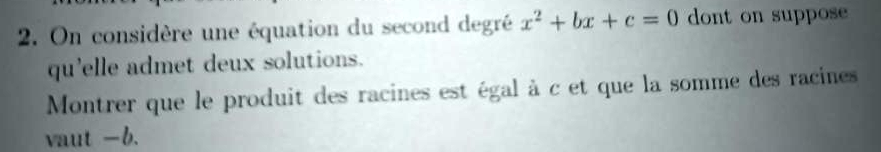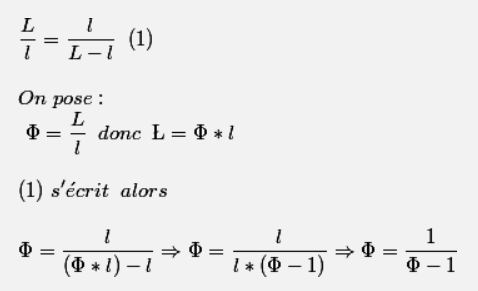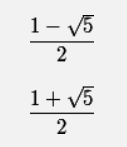PAVE

tu dois connaitre et pouvoir répondre aux questions que j'ai formulées dans mon précédent message....

Les abscisses des points d'intersection de la parabole P et de la droite D, s'ils existent, sont les SOLUTIONS de l'équation trouvée à la question2. Cette équation x²-mx +ma-a² = 0 est une équation de quel type ?? Ce type d'équation (que tu as étudié récemment) peut avoir : * aucune solution si .... ; dans ce cas la parabole et la droite n'ont AUCUN point commun. * ou une seule solution si ... ; dans ce cas la parabole et la droite ont un SEUL point commun. * ou DEUX solutions si ....... ; dans ce cas la parabole et la droite ont DEUX points communs. Si QUOI ???

Oui. On cherche une valeur xM donc une valeur de la variable x telle que f(x) = g(x). Il te faut résoudre l'équation f(x) = g(x). Cette équation s'écrit ici, avec f(x) =x² et g(x)= mx-am+a² (réponse de la question 1...) x²= mx-am+a² ce qui est pratiquement le résultat attendu (relis la question où la réponse est donnée ) Ensuite, on peut alors passer à la question 3 . Mais avant que penses tu de l'équation trouvée ? elle est de quel type ?

Pas possible.... dans un cursus scolaire normal. En 3ème on apprend à trouver le point d'intersection de 2 droites. En Seconde, on voit comment trouver les points d'intersection d'une parabole avec une droite ou une autre parabole. En 1ère je pense qu'avant de te donner un exercice avec des paramètres, on t'a fait réviser avec des fonctions simples. Tu n'as pas répondu à ma question purement mathématique : As tu vu, lu et compris les indications que je t'ai données dans mon message concernant la question 2 ? C'est la méthode classique qui permet de trouver les coordonnées des points d'intersection de 2 courbes représentant 2 fonctions f et g ; ces 2 courbes ont bien sûr pour équations y = f(x) et y =g(x) . As tu déjà fait des exercices simples sur ce thème ? Les abscisses de ces points (s'ils existent) sont les solutions de l'équation..... tout simplement f(x) = g(x)

As tu vu, lu et compris les indications que je t'ai données dans mon message concernant la question 2 ? C'est la méthode classique qui permet de trouver les coordonnées des points d'intersection de 2 courbes représentant 2 fonctions f et g ; ces 2 courbes ont bien sûr pour équations y = f(x) et y =g(x) . As tu déjà fait des exercices simples sur ce thème ? Les abscisses de ces points (s'ils existent) sont les solutions de l'équation.....

Si tu essayais de REDIGER en prenant pour MODELE l'exemple que je t'ai donné et expliqué en détails.... La droite de coef. directeur m (quelconque) qui passe par le point A(a;a²) a une équation de la forme y=mx+p. Pour calculer p, on utilise le fait que cette droite passe par le point A de coordonnées xA= a et yA =a² DONC que les coordonnées du point A "vérifient" son équation c'est à dire que yA = m*xA + p soit ici : a²= m*a+p d'où : p= a²-ma L'équation de la droite de coef . directeur m passant par le point A(a;a²) est : y=mx -am+a² Voilà une réponse RÉDIGÉE

oui mais comme tu n'as pas REDIGÉ, je suis incapable de savoir si tu as compris ou si tu as simplement utilisé le résultat qui est donné par l'énoncé.

Rappels de cours : Si le point M est un des points d'intersection de la parabole P avec la droite D, * le point M est un point de la parabole P donc ses coordonnées "vérifient" l'équation de la parabole ; on a yM = f(xM) et * le point M est un point de la droite D donc ses coordonnées "vérifient" l'équation de la parabole ; on a yM = g(xM). Les coordonnées du point M (si ce point existe) sont donc solution du système formé par les équations de la parabole et de la droite.

Bonjour, Quelques rappels de cours pour aider à faire la première question... RAPPELS (c'est du cours déjà vu...) 1) L'équation d'une droite dans un repère (cartésien) est de la forme y = mx +p m est le coefficient directeur de la droite (il caractérise la direction de la droite par rapport aux axes) p est l'ordonnée à l'origine (c'est l'ordonnée du point où la droite coupe l'axe des ordonnées ce point a pour coordonnées 0 et p) Une droite est parfaitement déterminée si on connait ces 2 coefficients m et p. 2) Pour tracer une droite 2 points suffisent. Si on connait l'équation de la droite, on peut facilement calculer 2 points de cette droite et la tracer. 3) Réciproquement si on connait les coordonnées de 2 points A et B d'une droite , on peut (si on connait le cours bien sûr) déterminer l'équation de la droite (unique ) passant par ces 2 points. On calcule m =(yB-yA) /(xB-xA) puis en utilisant soit A soit B, on calcule p. 4) On peut déterminer l'équation de la droite si on connait les coordonnées de l'un de ses points ET son coefficient directeur. Exemple simple : La droite de coef. directeur m= 5 qui passe par le point A(3;9) a une équation de la forme y= 5x+p. Pour calculer p, on utilise le fait que cette droite passe par le point A DONC que les coordonnées du point A "vérifient" son équation c'est à dire que yA = m*xA + p soit ici : 9= 5*3 +p d'où : p= 9-15 = -6 L'équation de la droite de coef . directeur 5 passant par le point A(3;9) est : y= 5x -6. Voilà une réponse RÉDIGÉE La question 1 de l'énoncé se traite comme l'exemple ci dessus mais avec des coefficients littéraux (paramètres m et a). Il en résulte que l'équation de la droite est exprimée uniquement avec des lettres. La réponse fournie par l'énoncé le confirme : y = mx -ma+a² (coef directeur m et ordonnée à l'origine a²-ma).... tout simplement 😟.

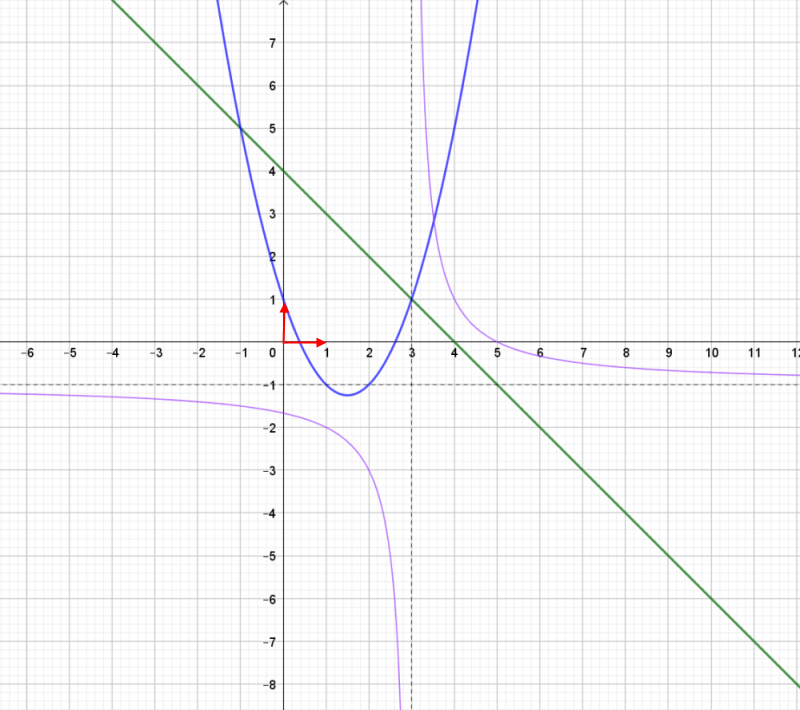
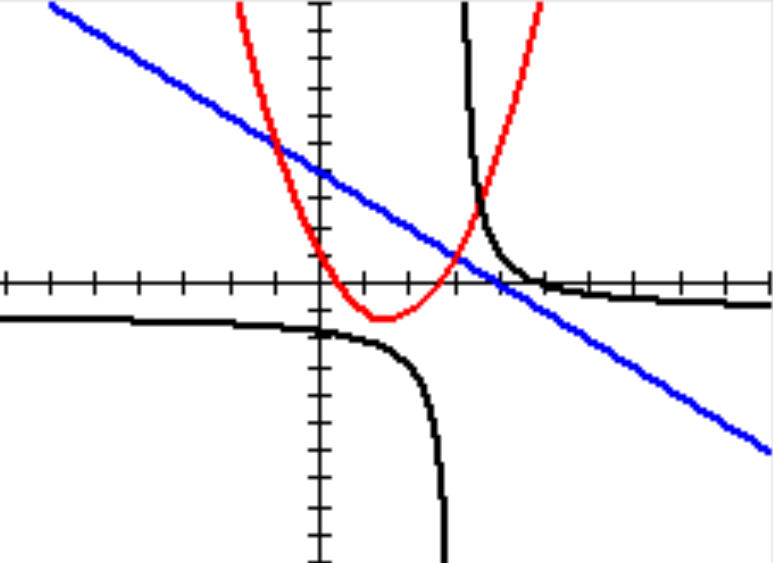
Bonjour, Juste pour le plaisir d'utiliser GEOGEBRA... tu pourras VERIFIER tes réponses suivantes. NB : les courbes qui se tracent sont celles de f(x)/20 et g(x)/20 (les ordonnées de M et P ont été divisées par 20)

@ Alyha Si un jour prochain, tu viens jeter un œil sur ce site, tu verras que 2 personnes (bénévoles !!) ont pris la peine d'essayer de t'aider. Dommage que toi tu n'aies pas eu le courage de leur répondre.... 😢

A l'avenir, ne mets qu'UN seul exercice par message. Sinon cela devient très vite CONFUS 🧐. Je t'ai déjà (et BlackJack) aussi !!) donné des indications sur cet exercice. Ce qu'il faut VOIR dans cet énoncé c'est que l'équation dont on parle n'est pas la forme générale ax²+bx+c = 0 mais un cas particulier pour lequel a = 1. As tu vu en cours les formules exprimant en fonction des coefficients a, b et c, la SOMME et le PRODUIT des racines d'un polynôme du second degré lorsque ces racines existent ? Si oui, quelles sont ces formules ? et c'est fini !! Si non, revois ce que Black Jack a fait.... donne les expressions des racines et calcule leur SOMME puis leur Produit.

Louis bonsoir, je prends le relai de Jules.... juste pour "mettre en forme" les calculs faits avec Jules. Quand on écrit un calcul "en ligne ", il n'est pas facile à lire (absence de trait de fraction entre autre mais aussi confusion entre la lettre minuscule l et 1 !)... Rien ne vaut un bon crayon et une feuille de papier ☹️ Le logiciel Latex permet de faire des belles formules mais c'est un peu long à mettre en œuvre 😟 A partir de la dernière égalité, en multipliant chaque membre par -1, on obtient : (-1) = 1 On développe le 1er membre puis on transpose le 1 dans le 1er membre (ou si tu préfères on retranche 1 à chaque membre de l'égalité) On obtient alors ²--1 =0 Je n'ai pas compris d'où tu sortais un 4 !! Les 2 solutions de cette équation du second degré sont en effet (1-5)/2 et (1+5)/2 On ne retient que la solution positive puisque est le rapport de 2 longueurs (donc positives).

Important : Pour voir la totalité du message que je t'ai envoyé, il faut cliquer sur le mot "expand" qui est l'équivalent de "pour voir la suite, cliquer ici".

Bonjour, Comme l'a dit Anylor dans le parcours 1, tu es amenée à étudier le signe de f'(x). Dans ton écriture finale de f '(x) tu as malencontreusement oublié de recopier l'exposant 2... s'il n'est pas trop tard...

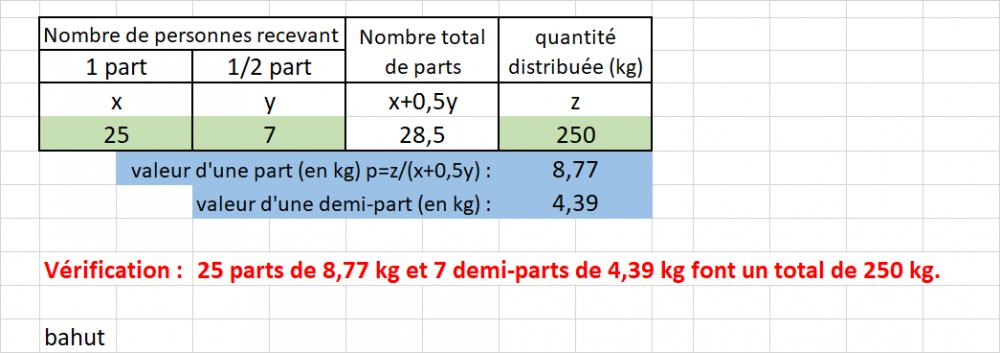
Bonjour, Pour compléter la réponse de Jules, je te propose de t'intéresser à la feuille de calcul ci-jointe (tableur). Cette feuille est protégée par un mot de passe (bahut) donc tu ne peux saisir des valeurs que dans les trois cellules vertes qui ne sont pas verrouillées. Tu peux tester cette feuille avec le deuxième exemple de ton énoncé. Les noms que j'ai attribués aux données (en fait il n'y en a que TROIS x, y et z) ne sont pas ceux utilisés par Jules mais la démarche est la même.... Valeur d'une part : z/(x+0,5y) EB210929 parts.xlsx Copie d'écran

Geogebra, tu verras, c'est super... Ne perds pas de vue cependant qu'aux examens, tu devras faire avec ta calculatrice 😯 !!

La figure réalisée avec GEOGEBRA.... c'est tellement plus beau que sur un écran de calculatrice 🤠 !

Après Casio, puis TI, je viens de faire avec Numworks.🧐

avec les couleurs 😄

Juste pour m'assurer que mon simulateur de calculatrice (il est vieux☹️...) fonctionnait encore. Je ne pourrai pas traiter ta question 2c car... je n'ai pas la couleur 🤭😂.

Je comprends mieux le niveau de ce DM 🤓... plus adapté à une entrée en Première qu'à une entrée en Seconde. Essaye de mettre ton profil à jour car il est toujours indiqué : classe de Seconde. Nous sommes à ta disposition pour t'aider.

Bonjour, Ce devoir comme tu le dis toi-même est un petit DM mais quand on commence l'année en Seconde, il y a beaucoup de choses à dire et surtout à FAIRE pour traiter ce devoir. Si tu veux que l'on puisse t'aider EFFICACEMENT, il faut que, pas à pas, tu nous dises ce que tu proposes comme réponse (on saura ainsi ce que tu sais !). On pourra alors corriger tes erreurs puis t'aider à mettre en place une solution complète et... rigoureuse. Si vraiment tu es en Seconde (et pas en 1ère ??), la simple représentation graphique à la main d'une fonction homographique n'est pas évidente ! Quand on sait faire (parce que l'on a déjà fait plusieurs fois !), bien sûr c'est... facile !! Et puis un logiciel graphique (ou une calculatrice graphique) quand on sait s'en servir, c'est très utile... A toi de nous proposer TES réponses.