PAVE

Bonsoir,

Je trouve que notre miss manque d'amour-propre. Elle est championne du "copié-collé" sur tous les sites de soutien scolaire environnants.

@Pzorba J'inverserais volontiers tes 2 verbes. A la fin d'un cours, il faut avoir compris et au début du cours suivant, il faut avoir appris 🤓. Bonne soirée.

Très prosaïquement, les 3/8 d'un demi-camembert (voire même les 5/8 d'un demi camembert) est ce plus ou moins qu'un demi-camembert ? Il faut que tu comprennes que les réels x dont on place les images sur le cercle trigonométrique, on les écrit sous forme de multiples (ou de sous-multiples) du nombre pi (qui est un nombre valant 3,1416....). Si on te demande de placer sur le cercle trigonométrique, l'image du nombre réel 2,35619449, tu vas t'arracher les cheveux alors que ce nombre n'est rien d'autre que l'expression décimale de 3*pi/4 ou encore (3/4)*pi... on tourne dans le sens positif de 3 fois un demi angle droit : 3 fois 45° (= pi/4 rad) soit 3 fois pi/4 soit 3*pi/4 = (3/4)*pi ! Prends la peine de vérifier avec ta calculatrice que : 3pi/4 = (3/4)*pi 2,35619449 Idem avec x= 1,570796327 qui n'est autre que pi/2 ; l'image de pi/2, c'est immédiat, celle du réel 1,570796327... moins immédiat et pourtant ces 2 réels sont égaux et ont la même image.

@volcano47, En Seconde on n'étudie pas la notion de dérivée. Je ne comprends pas pourquoi il serait incongru de demander un tableau de variation pour une fonction affine. En 3ème et en Seconde, quand on étudie (ou révise) les fonctions affines, on montre que le sens de variation de la fonction dépend du SIGNE du coefficient directeur de l'expression de f(x) (le petit a de ax+b). Je trouve même pédagogiquement pertinent de faire faire des tableaux de variation pour ces fonctions très simples : la droite qui "descend" ou qui "monte" préfigure bien ces flèches que l'on met dans les tableaux de telles fonctions. @ _mochi- Pour moi, il n'y a pas d'ambiguïté ; la fonction que tu as à étudier est bien la fonction affine définie par f(x) = 6-2x et dessiner son tableau de variation ne pose aucun problème en utilisant pour ce faire le signe du coefficient directeur (résultat en principe acquis en 3ème et conforté dans les révisions de Seconde). Je pense que toi tu as vu mon message contenant la représentation graphique de f et.... le tableau de variation correspondant. Si tu as encore des doutes ou des questions, n'hésite pas à les exprimer. Bon courage à toi qui habite dans un si bel endroit 🙂.

Reste calme 🙂, je suis prêt à t'aider bien sûr. Essaye de répondre aux questions que je t'ai posées.... Fonction affine : tu connais ? Sa représentation graphique ? Dis moi ce que tu sais sur cela. A toi.

Bonjour, Si f(x) = 6-2x tu as déjà vu des fonctions de ce type en 3ème. 6-2x peut s'écrire -2x+6 et sous cette écriture, on reconnait une expression de la forme ax+b (forme générale d'un binôme du 1er degré) donc f(x) = -2x+6 est une fonction affine. A quoi ressemble la représentation graphique d'une fonction affine (voir ton cours de 3ème, peut-être révisé en début d'année de Seconde) ? Trace cette représentation graphique et montre nous ce que tu obtiens...

Tu vas fâcher Pzorba 😟... tu ferais mieux de croire ce qu'il te dit 😄. 3*pi/8 = (3/8)*pi < pi car 3/8 <1 5*pi/8 = (5/8)*pi < pi car 5/8 <1 Nb : pi/8 c'est la moitié de pi/4 ! ça c'est pour construire les images des réels 3*pi/8 et 5*pi/8 sur le cercle

1) Donc nous sommes d'accord pour la question 1. 2) Comment as tu résolu la question 2 ? Et comment passes tu à la réponse suivante (question3) Ta question est incompréhensible. Pourquoi et à propos de quoi poses tu cette question ?

oui bien sûr !! alors REMPLACE...

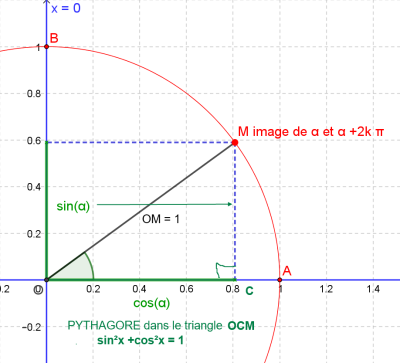
Je pense t'avoir déjà dit d'écrire des égalités et pas des bouts de trucs à la queuleuleu... Une des relations principales (cours de 3ème) qui t'a été rappelée il n'y a pas longtemps est [sin(x)]²+[cos(x)]² = ?????

Tu vas aller "faire de la barre" ?🏋️‍♀️

Qu'attends tu ensuite pour REMPLACER avec les valeurs trouvées en 1a) ?

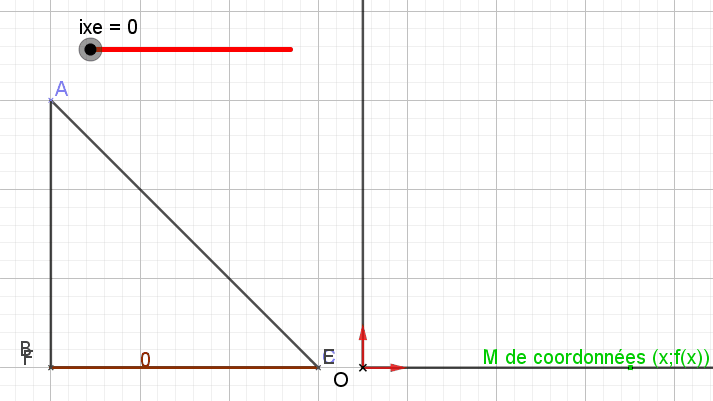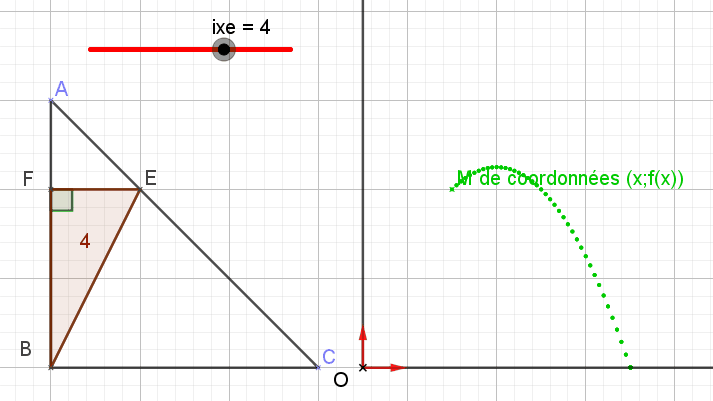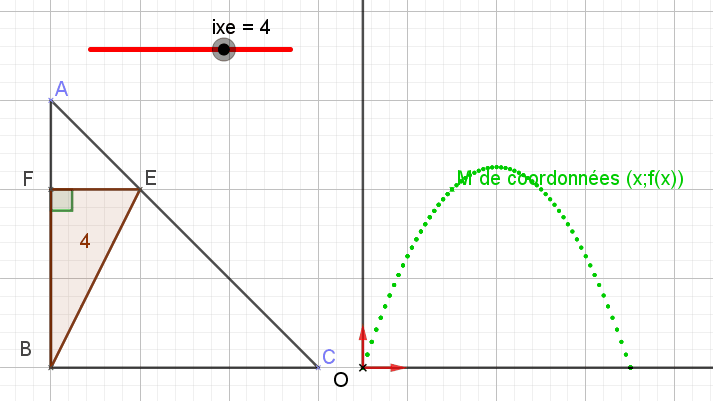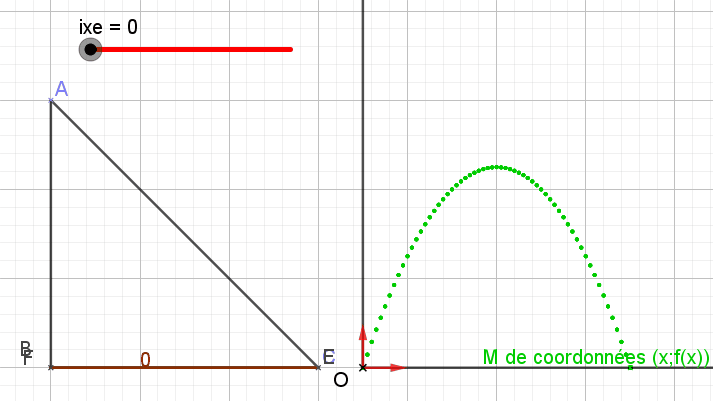
Oui donc le calcul de la distance entre I et M s'en déduit... la réponse bien sûr est fonction de x. A toi.

Bonjour, Partie A Tout d'abord, qu'as tu répondu à la question 1a ) ? Ensuite pour la 1b), la distance entre 2 points dont on connait les coordonnées (voir 1a) dans un repère orthonormé se calcule grâce à une formule... en principe bien connue.

Bonsoir, Quelques idées pour BIEN faire : 1) si on vient de te "donner ça pour demain" (!!), tu pourras toujours dire que cela n'est pas sérieux et qu'il te faut du temps pour traiter correctement ce problème. 2) ce n'est en allant ramasser ici ou là , le corrigé de ce problème et en le recopiant vite fait, que tu vas PROGRESSER. Si tu n'as qu'une demi heure à consacrer à la recherche des solutions, alors FAIS LE mais sérieusement. Tu ne feras peut-être pas grand chose mais cela te sera plus profitable que de passer une demi heure à RECOPIER (bêtement bien sûr) le travail de Palo_3, si tant est qu'il existe ce travail.... Si tu veux que l'on t'aide, tu peux nous écrire ce que tu as COMPRIS ou pas compris dans les questions posées. A toi de FAIRE et nous on t'aidera à AVANCER. A bientôt ? PS : tu peux aussi essayer de répondre à mon premier message (du 26 décembre) tout en haut du fil.

GEOGEBRA bis 🙂 et Zoom zoom Zoom

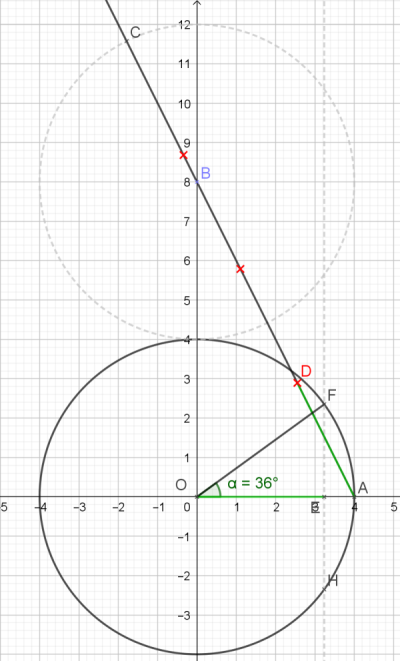
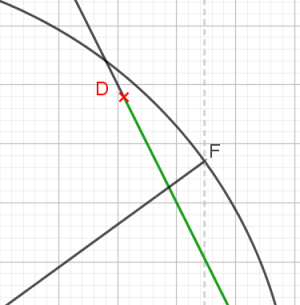
Merci à vous deux pour ces échanges. Comme Jules, je n'avais jamais encore rencontré cette construction. Curieux de nature mais un peu flemmard aussi (de nature ?), remettant à plus tard une démonstration, je me suis contenté hier soir de faire la construction avec GEOGBRA. Déception, l'angle obtenu ne mesurait pas 36 ° !!!! Comme Jules, j'avais fait confiance à mes yeux et placé le point D sur le cercle. Erreur fatale.... Rassurez vous, ce cuisant échec ne m'a pas empêché de bien dormir 😁.

César bien sûr 😄. Le notre est classé X mais il n'en est pas moins glorieux (voir le troisième message, il y a 6 heures).

Pour les multiples de /5, il est plus difficile de "graduer" le cercle mais, si on s'y frotte un peu, on comprend (vite ?) qu'en "parcourant" 5 fois /5, on aboutit à l'image de... ! 6*/5 peut s'écrire 5*/5 +/5 soit 6*/5 = +/5 donc on a 2 nombres de la forme x et +x..... Petit schéma général pour x et +x ou formules de Jules....

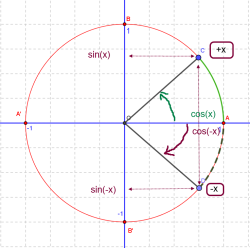
Si on ne connait pas la notion de mesure principale d'un angle, on peut essayer de positionner les réels sur le cercle trigonométrique... Avec des multiples de /8, cela est faisable. Tu "sautes" de /8 en /8, ------> 3 fois dans le sens positif pour atteindre 3*/8 ------> 3 fois dans le sens négatif pour atteindre - 3*/8. et graphiquement les réponses sont accessibles... mais est-ce suffisant pour le prof ? Plus expéditif (et plus satisfaisant !) les 2 nombres 3*/8 et - 3*/8 sont 2 nombres réels opposés donc leurs cosinus sont .... et leurs sinus sont .... confère les 2 premières formules de Jules sin(-x)=-sin(x) cos(-x)=cos(x) qu'un petit schéma (général) permet de retrouver... vite fait 🙂.

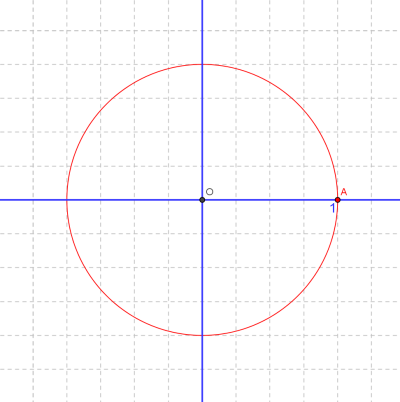
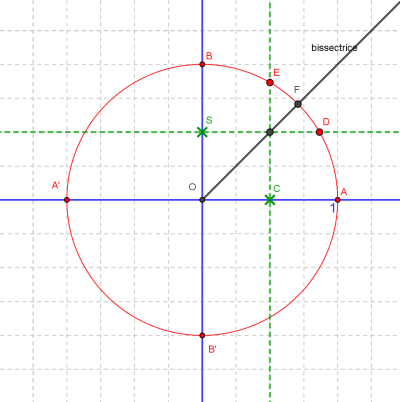
Pour construire rapidement un cercle trigonométrique de qualité, il suffit de disposer d'une feuille (de préférence quadrillée avec des petits carreaux, cela facilite la...vie !) et d'un compas. 1) tracer les 2 axes et noter O le point d'intersection. 2) choisir une unité de longueur OA sur l'axe des abscisses (futur "cosinus) (prendre si possible un nombre pair de petits carreaux ce qui permettra d'obtenir facilement le milieu du segment [OA]...) 3) tracer le cercle de centre O et de rayon OA. 4) placer les points A', B, B' et déterminer les milieux des segments [OA] et [OB] (c'est immédiat si le nbre de petits carreaux est pair). 5) tracer les droites perpendiculaires aux axes à partir des milieux des segments [OA] et [OB]qui coupent le cercle en 2 points du 1er quadrant, lesquels sont les images des nombres /6 et /3 6) pour avoir l'image de /4, le tracé de la bissectrice est immédiat.... 7) A partir des points obtenus sur le premier quadrant, on peut facilement compléter le cercle trigonométrique.... et faire figurer les "valeurs particulières classiques" dont on a besoin. NB : la figure est plus rapide à faire qu'à décrire....

Bonjour, Un élève de Première (ou Terminale ?) a déposé sur ma messagerie privée le sujet suivant avec pour questionnement : "Je ne comprends pas comment on fait pour placer les réels des questions 2 et 4. Pouvez-vous m'expliquer svp ?" A noter par ailleurs qu'il a joint à cette demande, ses réponses écrites aux autres questions... ce qui est fort bien 😀 ! Il a par ailleurs tracé avec plus ou moins (plutôt moins 😟) de réussite et de précision, des cercles trigonométriques pour conforter ses réponses, ce qui est là encore fort bien. Je me propose d'expliquer comment tracer un "beau" cercle trigonométrique et y placer rigoureusement les valeurs "classiques" (/6 ; /4; /3) dans le premier quadrant. Il faut hélas pour cela disposer comme à l'école primaire d'un COMPAS... en état de marche !! Mais commençons par répondre au souci de notre élève : Pour /8, on remarquera que /8 est la moitié de /4.... Pour /5, c'est plus compliqué... le temps étant en général compté, on bricole entre /4 et /5 (😒) ou on sort vite fait son rapporteur... ("c'est quoi ce truc ?") A suivre

Ich bin darüber ganz einverstanden !