PAVE

😄 Peut-être qu'il y a 60 ans, quand j'avais ton âge, j'ai eu moi aussi des moments difficiles.... y compris en maths. Il n'y avait pas internet et le soutien scolaire en ligne, on ne pensait même pas que cela puisse exister un jour. Cela ne m'a pas empêché de devenir prof de maths 🤓. Depuis quelques années déjà à la retraite, j'entretiens mes neurones en les faisant travailler régulièrement tous les jours en aidant (bénévolement) sur des sites comme e-bahut. Question classique : quel est l'âge du capitaine ?

Ouf !! nous voilà au bout. As tu conscience du temps passé pour résoudre ce "petit" exercice.... Cela n'est pas normal. Certes cet exercice est difficile à mon avis à cause des 2 paramètres !! Mais son niveau n'est pas adapté à TON niveau. Je t'ai "trainé" de question en question et tu buttais sur les méthodes de base que manifestement tu ne maitrisais pas. L'étude de la position relative de 2 courbes, par exemple, est UN CLASSIQUE mais pour une première expérience mieux vaudrait prendre 2 fonctions classiques et ne pas y mettre des paramètres. Si tu es malin, en mettant bout à bout les éléments de réponses que je t'ai, au final, donnés , tu vas avoir un "bon devoir" et une bonne note. mais fondamentalement qu'as tu compris ? qu'as tu retenu ? Tente l'expérience : cache tous tes brouillons et reprends entièrement ce devoir, pour voir ce que tu seras capable de refaire SEUL. Je te dirais volontiers de ne recopier que ce que tu as compris ; tu sais ton prof ne sera pas dupe, il lui suffira de t'envoyer au tableau pour la correction.... il verra très vite que tu as été (très) aidé. Voilà c'est dit. Tu as le mérite de la persévérance et le courage de te battre ; cela c'est bien, il faut continuer ! Peut-être aussi que tu ne seras pas le seul dans ta classe à avoir "galéré"... sur ce devoir. Bon courage.

Pourquoi reviens tu toujours à ce -b/(2a) . Explique pourquoi et qu'est ce que tu cherches. Arrête d'écrire des "je fais" "je remplace" "on fait avec la formule" qui n'expliquent RIEN. REDIGEZ c'est explique, JUSTIFIER en citant une propriété ou un théorème Exple : Si le discriminant d'un polynôme du second degré est égal à 0, ce polynôme admet une SEULE racine qui est égale à x0 = -b/(2a) Le trinôme x² -2ax + a² a une seule raine x0= (2a)/(1*1) = a donc il peut s'écrire x² -2ax+a² =(x-a)² (on aurait pu DIRECTEMENT obtenir ce résultat sans calculer le discriminant en remarquant l'identité remarquable : x²-2ax+a² = (x-a)² car A²-2AB + B² = (A-B)² donc pour toute valeur de x (sauf a) f(x)-d(x) est POSITIF (c'est un CARRÉ) donc f(x) > d(x) donc Parabole au dessus de Tangente . oui mais lis ce que j'ai REDIGE ci dessus !

Cherche dans ton cours de 1ère un paragraphe intitulé : Factorisation d'un polynôme du second degré : Si = 0, une seule racine x0 et alors P(x) = a (x-x0)² [c'est le cas dans ton exercice question 4) Si >0, le polynôme a 2 racines x1 et x2 et alors P(x) = a (x-x1)(x-x2) Si <0, le polynôme n'a PAS de racines et alors le polynôme n'est pas factorisable.

Non ! Tu ne lis pas ce que j'écris....

d(x) = 2ax-a² OUI on est d'accord f(x)-d(x) = x² -(2ax-a²) je supprime la parenthèse qui est ici précédée d'un d'un signe "-" donc... cours de 4ème. = x² -2ax +a² Ce trinôme du second degré (forme ax²+bx+c) a pour coefficients a= 1 b= -2a c= a² (avec c=a² et non -a², on a un discriminant qui vaut cette fois 0) Il te faut factoriser ce trinôme du second degré pour pouvoir étudier son SIGNE suivant les valeurs de x. Je m'absente 2 heures au moins

La citation faite dans ton dernier message, je ne l'ai pas retrouvée dans le fil ☹️ mais peu importe, puisque la dernière ligne est fausse. " -a² Si tu écrivais des EGALITES 😶. d(x) = 2ax-a² OUI on est d'accord f(x)-d(x) = x²-2ax-a² FAUX De plus, ton calcul du discriminant à partir de ce résultat faux contient une nouvelle erreur car si a= 1, b=-2a et c= -a² , on doit obtenir delta = (-2a)² - 4*(1)(-a²) = 4a² -(-4a²) = 4a² + 4a² = 8a² Ces réponses ont déjà été écriteS. Je ne les ai pas vues passer !! " Il faut étudier le SIGNE de l'expression obtenue après correction ; c'est bien un trinôme du second degré (forme ax²+bx+c) avec a= 1, b=-2a et c= ????? Connais tu le théorème qui donne le signe d'un trinôme du second degré (c'est du cours de 1ère).

Tes 2 derniers messages ne sont pas cohérents. Si tu répondais posément à mes questions au lieu de partir dans tous les sens sans logique.

Oui. Mais tu peux simplifier cette écriture d(x)=2ax ..... complète sachant que -2a²+a² = ?? Ensuite tu calcules f(x) - d(x) = ????? et il reste à étudier le signe de l'expression trouvée pour f(x) - d(x).

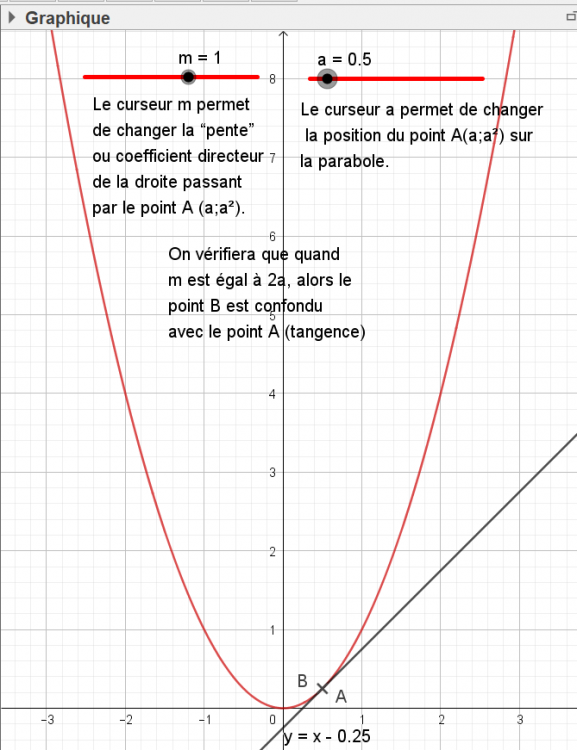
Il faut poursuivre : On a montré que si m = 2a, cette droite D d'équation y= mx-am+a^2 n'avait qu'un seul point commun avec la parabole (question 3). L'équation de la droite D lorsqu'elle est TANGENTE à la parabole s'écrit donc :????? Il suffit de remplacer m par 2a pour avoir l'équation de la droite tangente en A(a;a²) à la parabole P. Pour cette tangente que vaut d(x) ???? As tu essayé de voir la figure interactive avec GEOGEBRA ?

oui mais quelle est l'expression de d(x) en fonction de x ?

Pense à développer le texte complet de mon message en cliquant sur le mot Expand 🤓.

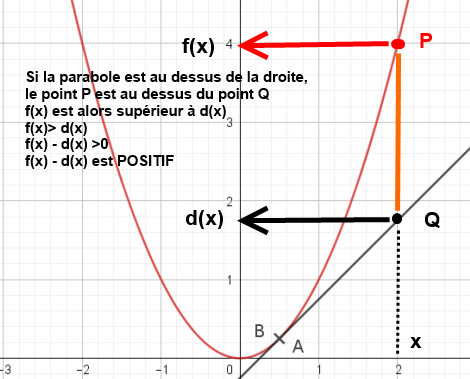
Pour la question 4, il faut que tu comprennes ce qui est "montré" sur la figure ci dessous. Résultat à connaitre : Pour étudier la position relative de 2 courbes Cf et Cg, l'une représentant une fonction f et l'autre une fonction g, on étudie le signe de la différence f(x) - g(x) Si sur un intervalle f(x)- g(x) est positif, alors f(x) >g(x) donc Cf est au dessus de Cg Si sur un intervalle f(x)- g(x) est négatif, alors f(x) <g(x) donc Cg est au dessus de Cf Rappel : Si pour une valeur de x, f(x)- g(x) est nul, alors f(x)= g(x) donc Cf et Cg se coupent au point commun d'abscisse x. Bonne nuit.

J'étais parti cueillir des pommes !!!! Oui ... et non : c'est m=2a Ensuite ce résultat est donné dans l'énoncé de la question : il serait intéressant que tu nous dises comment tu es parvenu à ce résultat. Quelle démarche et quel calcul ? Tout particulièrement pour la question 4, il te serait utile d'ouvrir le fichier GEOGEBRA que j'ai mis en ligne dimanche à 18h24. Voilà une (triste) copie d'écran de ce l'on peut voir..... un exemple parmi une infinité !!

Bonjour, Pour la question 3, tu as déjà toutes les indications nécessaires. Rappel : 1) La parabole et la droite auront UN SEUL point commun si et seulement si l'équation x²-mx+ma-a²=0 a une SEULE solution donc si le discriminant de cette équation en x est égal à ZERO. 2) Il faut en conséquence que tu calcules le discriminant de cette équation. équation : x²-mx+ma-a² = 0 coef de x² = 1 (a=1) coef de x = -m (b= -m) terme constant = ma-a² (c=ma-a²) discriminant m =(-m)² -4*(1)*(ma-a²) = m² -4(ma-a²) = m²-4am +4a² /!\ La première réponse que tu avais donnée (dimanche 15h46) était fausse ; j'avais laisser passer ce résultat faux et pire... je l'avais recopier dans mon message de dimanche 17h56 😢. Intervenant trop tard je n'ai pas pu éditer et corriger ce message. D'où le récapitulatif (correct !!) repris ci- dessus.

Comme tu veux. Volcano dans son message t'a donné une factorisation de m.... Pour le détail de ce calcul, tu peux aussi revoir la partie A que tu as traitée avec Jules dans un fil précédent.

J'ai effectivement laissé passer une erreur de calcul dans ton calcul du discriminant en m. Merci Jules. J'ai rectifié dans mon message précédent. Pour éviter toute ambiguïté, je récapitule : équation : x²-mx+ma-a² = 0 coef de x² = 1 (a=1) coef de x = -m (b= -m) terme constant = ma-a² (c=ma-a²) discriminant m =(-m)² -4*(1)*(ma-a²) = m² -4(ma-a²) = m²-4am +4a²

Pour ceux que la traduction graphique de ce problème intéresse... EB211010.ggb

!!! qui ? quoi ?? Si tu faisais des phrases.... Tu fais souvent des citations inutiles alors qu'ici par exemple en reprenant ma phrase et en la complétant, tu aurais une rédaction complète et cohérente. "La parabole et la droite auront UN SEUL point commun si et seulement si l'équation x²-mx+ma-a²=0 a une SEULE solution donc si le discriminant de cette équation est égal à ZÉRO" Le calcul du discriminant donne effectivement l'expression delta = m²-4am-a² , laquelle dépend des paramètres m et a. Dans la question 3 on te demande de trouver pour quelle valeur du paramètre m, la parabole et la droite ont un seul point commun. Un seul point commun => une solution UNIQUE => = 0 => on cherche m tel que m²-4am-a² = 0 NB : m²-4am-a² est un polynôme du second degré par rapport à m donc m²-4am-a² = 0 est une équation du second degré dans laquelle m est l'inconnue... tu dois savoir résoudre cette équation du second degré (là encore tu as la réponse finale dans l'énoncé). Je te laisse finir.

La parabole et la droite auront UN SEUL point commun si et seulement si l'équation x²-mx+ma-a²=0 a une SEULE solution donc si le discriminant de cette équation est égal à ???? Pense aussi à prendre l'air 🤠.

Il fait un temps superbe 😀. Pour ma santé physique et mon équilibre mental 🐭, je vais aller prendre l'air une heure ou deux..... oui calcule le discriminant avec ces valeurs.

bien sûr que.... NON si a = 1, b = -1 et c = -1, l'équation serait x²-x-1 = 0 ce qui n'est pas le cas. Rappel x²-mx+ma-a²=0 le coef de x² est effectivement 1 le coef de x est ????? et le terme constant est ????

a est le coefficient de x² donc a= ????? b est le coefficient de x donc b= ????? c est ce qui reste (le coefficient du terme ne contenant pas x) donc c= ?????

La seule chose valable dans ta réponse est le mot discriminant