PAVE

@Nathoune Quel dommage que tu n'aies pas eu le courage de poursuivre ton travail... ☹️ Nous, on était disposés à t'aider et surtout à te faire progresser. C'est raté 😢 En cadeau d'adieu.... une image que j'avais préparée spécialement pour toi 🐭 Bon courage quand même.

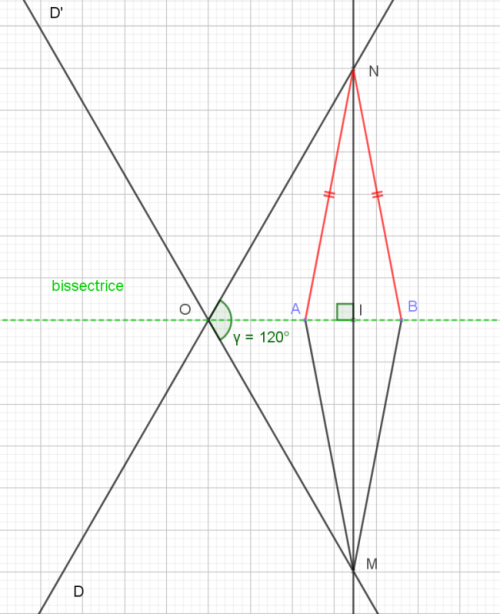
Petite suggestion, avant que je me déconnecte : on te parle de I milieu du segment [AB].... comment s'appelle la droite perpendiculaire en I au segment [AB] ? trace la.... A demain, si tu veux.... PS : quel est ton niveau d'étude ?

Bonsoir, Tu as bien sûr fait une belle figure. Pourrais tu nous la montrer (scan ou photo mis en pièce jointe dans ton prochain message) ? a) Si le triangle AMB est isocèle en M, quelle égalité peut-on écrire ?

suite

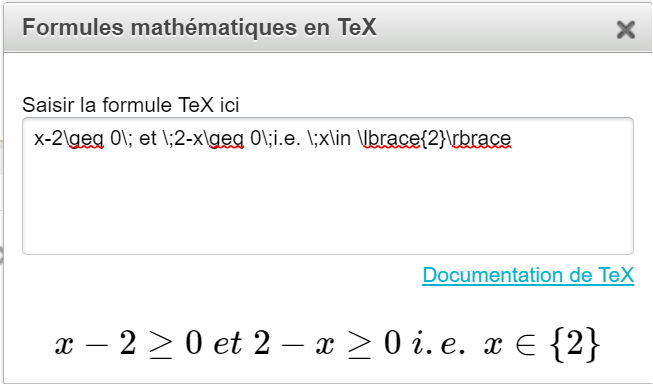
@Chaka Juste pour me faire une idée du problème Latex 🧐 \(x-2\geq 0\; et \;2-x\geq 0\;i.e. \;x\in \lbrace{2}\rbrace\) Pourquoi des dollars $ dans ton code Latex ? NB : Les parenthèses ouvrante et fermante à chaque extrémité du code ont été ajoutées par ... le site.

En relisant ta demande initiale, je m'aperçois que tu parles de "mensualités" ; je complète en conséquence mon message précédent... Si le remboursement se fait par mensualités constantes, la formule est la MÊME et la démarche identique. Il faut cependant bien adapter les paramètres utilisés dans la formule : * n est le nombre de mensualités * t est le taux MENSUEL Attention, si le taux donné ta est un taux annuel, il faut calculer le taux mensuel t équivalent avec la relation : 1+ta =(1+t)12 =>1+t = (1+ta)1/12 => t=(1+ta)1/12 -1, formule que tu retrouveras dans le document que Denis t'a signalé.

Bonjour, Tout dépend du mode de remboursement ! Pour un remboursement par annuités constantes, regarde la feuille de calculs jointe... Le résultat (montant de l'annuité constante) est sans grand intérêt ; il est plus important de comprendre comment est construit le tableau de remboursement de l'emprunt. Amuse toi bien 🤓 et si besoin d'explications, on peut assurer le service après vente 🤭. Math fi rembourst d'emprunt par annuités constantes avec graphique.xlsx

Bonjour, La lecture du fil ci dessous pourrait peut-être t'être utile : https://www.e-bahut.com/topic/57858-continuité-des-fonctions-variable-réelle/

Merci Jules d'avoir signalé le problème de "mon" lien... J'ai corrigé dans mon précédent message et je l'insère ici à nouveau. https://www.youtube.com/watch?v=Z_BDJaveZNs Merci à nos collègues lillois pour ce "partage" youtubien 🤓 !!

Il y a une petite heure (?), tu sembles être passé voir si TON travail avait avancé....😟. Si tu ne réponds pas à nos questions, nous, on ne bouge plus 😷. Sur Internet, on trouve tout ce dont tu as besoin ! encore faut-il aller chercher les explications souvent très bien illustrée comme dans la première partie de ce tuto... et faire l'effort de comprendre (papier et crayon en main !). https://www.youtube.com/watch?v=Z_BDJaveZNs

Bonjour Linajj, As tu compris : a) à quoi sert cette méthode de Newton ? b) et comment elle "fonctionne" ? C'est cela l'essentiel .... Si oui, as tu répondu à la première question ?

Comme te l'a dit Jules, c'est du cours... presque à l'état pur 🤓. Tu dois avoir dans ton cours ou dans ton livre un paragraphe t'expliquant comment avec une intégrale, on peut calculer l'aire d'une portion de plan. Un théorème formalisant la démarche ? Que dit-il ?? Tu dois avoir aussi quelques exemples élémentaires. Je te propose pour introduire la suite de ton exercice, de nous dire comment dans la figure ci-dessous, tu calcules l'aire de la portion de plan "colorée". Essaye et dis nous ta démarche et si possible ton résultat....🙄.

Je suppose que l'énoncé est exp(x)x qui peut s'écrire aussi e^x≥ 𝑥 ou encore ex≥ 𝑥 ?? Et pas le produit du nombre e 2,71828 par x....

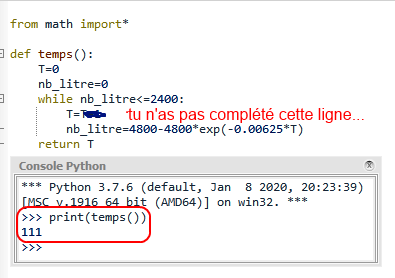
@kylian Dommage de t'arrêter en (si bon) chemin... Pour le script Python, compléter sur le papier est frustrant. Ce qui est le plus intéressant c'est de TESTER le script en "réel" (!!)...

En complément à mon précédent message.... 1ère méthode : P(X>3) = P(X=4) + P(X=5) 2ème méthode : P(X>3) = 1-P(X3) = 1- [P(X=0) + P(X=1)+P(X=2)+P(X=3)] "A la main", mieux vaut la 1ère méthode !! Mais j'allais le dire quand Jules est venu confirmer mon "sentiment", les calculatrices actuelles (donc pas les miennes qui ne donnent rien pour la loi Binomiale) ne donnent que P(X<k) !!!

Bonsoir, Je ne comprends pas ton problème. Si n n'est pas très grand, un calcul exacte est faisable.... Si la variable aléatoire X suit la loi binomiale de paramètres n (nombre de répétitions de l'épreuve de Bernoulli) et p (probabilité d'un succès lors de l'épreuve de Bernoulli), la formule qui donne la probabilité d'obtenir k succès (donc k est un entier !) au cours des n répétitions est : P(X=k). Pour calculer des probabilités que Xk [ou en adaptant X>k], on décompose l'événement (Xk) en la réunion de (k+1) événements 2 à 2 incompatibles (Xk)= (X=0)U(X=1)U.... (X=k-1)U(X=k) et donc P(Xk)= P(X=0)+P(X=1)+.... +P(X=k-1)+P(X=k) Il n'y a pas de formule donnant directement et exactement P(Xk) Exple avec n =10 !!: X suit B(10; 0,25) P(X<3) = P(X=0) + P(X=1) + P(X=2) Par contre pour P(X<9) = P(X=0) + P(X=1) + P(X=2) +..... +P(X=8) Bonjour la galère : 9 termes à calculer et à additionner ! On préférera dans ce cas P(X<9) = 1-P(X9) événements contraires = 1 - [ P(X=9) + P(X=10)] seulement 2 termes à calculer puis à soustraire APRES bien sûr -si n est grand- on peut approximer avec, par exemple, une loi normale si les valeurs de n et p le justifient et le permettent.... mais c'est une autre affaire. Pas sûr que cela réponde à ta question

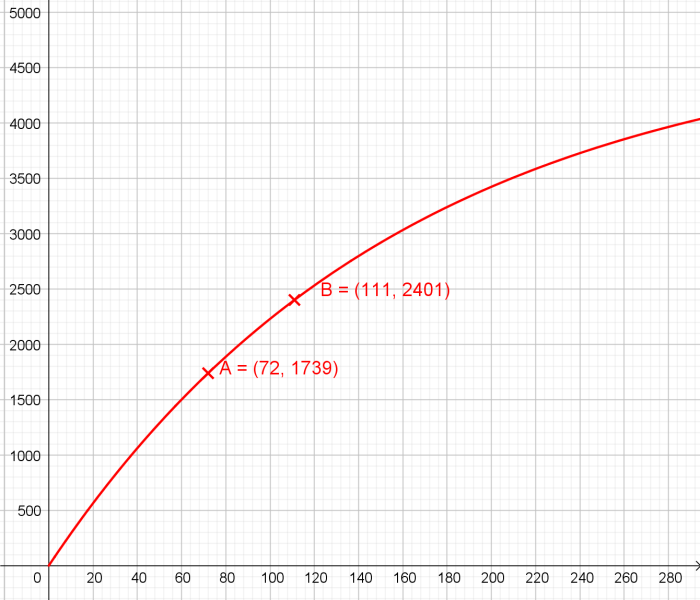
Courbe représentative de f réalisée avec GEOGEBRA (bonjour Denis 🤓) Par ailleurs, as tu TESTÉ le script en Python que tu as complété ? Enfin tu devrais "surveiller" ton orthographe car la première phrase de ton premier message est de ce point de vue calamiteuse (voir ci-dessous)...😟

lis d'abord mon précédent message

Bonjour, Je n'ai pas relu ton devoir (pas le temps) mais mes yeux se sont arrêtés sur la partie ci-dessous.....

Bonjour, C'est quoi l'ex 3 ? La question 3 ? Je ne vois pas ce que tu attends de nous..... Si tu sais te servir de ta calculatrice, il n'y a aucune difficulté dans cet exercice. Précise ce que tu as fait et ce que tu as déjà trouvé PUIS dis nous où est TON problème....

Il y a sur Internet des tas de vidéos expliquant comment on se sert d'un rapporteur... Par exemple :

Pourquoi ne pas essayer de faire ce que je te dis en construisant pas à pas la figure.... relis mes messages précédents. Moi j'en suis à la construction du point mobile M 🙄. Et j'attends toujours que tu m'envoies le fichier .ggb que tu devrais avoir essayé de faire en suivant mes instructions et en regardant le modèle simple que je t'ai donné hier. Toi tu me renvoies une copie d'écran sans intérêt puisque ce n'est pas toi qui a fait cette figure.... compliquée. Vouloir comprendre la construction en regardant la fenêtre Algèbre (voire même le Protocole de construction) ne me semble pas raisonnable pour qui ne maitrise pas les outils de GEOGEBRA.... Mieux vaudrait apprendre à te servir de ces outils de construction en pratiquant toi même ! Pour répondre néanmoins à tes questions, les objets que tu évoques sont des petites choses tout a fait secondaires (pour ne pas dire sans intérêt). Par exemple les "vecteurs" sont de simples flèches mettant en vis à vis les extrémités des 2 alignements de rectangles et de carrés ! On aurait très bien pu s'en passer mais je voulais... faire "joli" !! Voilà. Envoie moi ton fichier GEOGEBRA avec le point M si tu veux poursuivre.... Bonne nuit.

On continue ? Tu sais, GEOGEBRA est un très bon logiciel de géométrie mais aussi de représentation graphique. Il est facile à utiliser mais bien sûr, il faut prendre le temps de découvrir pas à pas les outils qu'il met à notre disposition. Terminale en Belgique, c'est à quel âge ? Pour situer ton niveau, si je dis fonction dérivée, tu connais ? fonction logarithme ? Bonne journée.

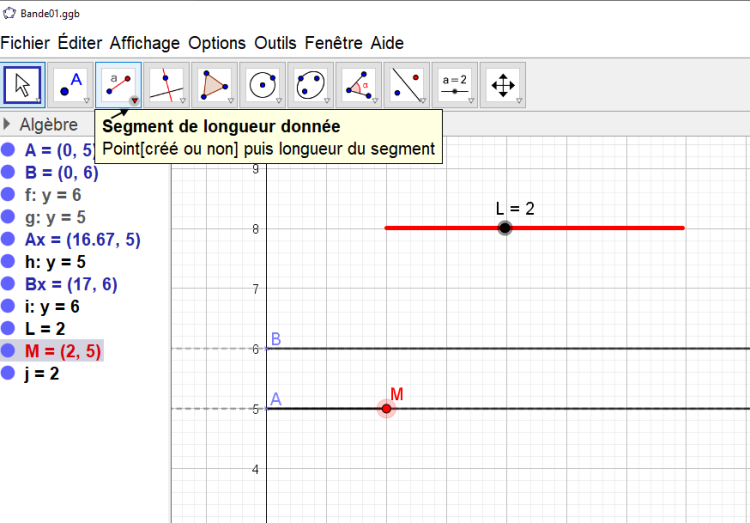
Je te propose d'essayer de mettre en place un rectangle de longueur L sur la figure GEOGEBRA du fichier joint. Création du curseur Ouvre ce fichier. Bande01.ggb Avec l'outil curseur (tu sembles l'avoir trouvé 🙂), tu crées un curseur L : L varie de 0 à 5 avec un pas de 0,5. On fait varier la valeur de L en déplaçant le curseur avec la souris. Essaye.... Tu fais défiler les valeurs de la variable L Construction d'un point mobile M tel que AM = la valeur de L Sur la demi-droite [A;Ax), on veut placer un point M se trouvant à la distance.... L du point A. On choisit l'outil "Segment de longueur donnée". On montre le point A, GEOGEBRA demande alors la longueur du segment ; on répond.... L. Un point apparait à la distance L du point A. Si tout s'est bien passé, ce point se déplace quant tu fais varier le curseur donc le nombre L. Tu peux essayer... si tu veux bien sûr.