julesx

Ça, c'est une primitive de le la fonction à intégrer. Il reste à calculer l'intégrale correspondante entre 0 et 1.

Tu as parfaitement le droit de le faire, mais ce serait mieux alors de dire que tu t’arrêtes pour le moment, ça évite aux intervenants d'attendre en vain une réaction. Cela dit, tu as enfin trouvé le résultat de l'intégrale ?

P.S. à 20h30: Je continue à ne pas comprendre ta démarche. On te donne une piste de réponse mais tu ne réagis pas. Tu attends quoi, de ce site ?

En fait, dans ce que j'ai écrit il faut remplacer x par t et lire une primitive de 1/(4-t2) est 1/4*ln[(2+t)/(2-t)]

Mais tu dois savoir que l'intégrale de la dérivée dune fonction est cette fonction ! Donc le résultat est 1/4*ln[(2+x)/(2-x)] à prendre entre 0 et 1. A toi pour le calcul.

Donc, tu peux calculer l'intégrale, puisqu'elle est de la forme somme(f'(x))

J'ai vu que tu es revenue de temps en temps. Tu en es où ?

Bonsoir, As-tu calculé la dérivée demandée à la question 1 ? Si tu oui, ne vois-tu pas le lien avec l'intégrale à calculer à la question 2 ?

De rien, bonne continuation.

Bonjour, On le sait parce qu'on a précisé au départ "On note p un nombre premier, p>3". Ensuite, on montre simplement que si r=0, 2, 3 ou 4, p ne peut pas être premier, donc ne répond pas à l'hypothèse que départ. Par contre, comme r=1 ou r=5 ne sont pas incompatibles avec l'hypothèse p premier, on en conclut qu'il existe bien des nombres premiers tels que p=6q+1 ou p=6q+5. Pour info, les premiers entiers donnant les bons restes sont 7, 11, 13, 17, 19, 23, 25, 29, 31, 35... Tu vois que, déjà là, apparaissent des entiers non premiers qui répondent à la condition sur le reste et qu'il est impératif de précisé au départ qu'on part d'entiers premiers.

Bonsoir, • En déduire que si p est un nombre premier strictement supérieur à 3, alors il existe q appartenant à N tel que p=6q+1 ou p=6q+5 Tu sais que 0<=r<=5. D'autre part, si r=2 ou 4, p est pair et si r=0 ou 3, p est divisible par 3, quelles possibilités te restent-ils pour que p soit premier ? • Démontrer, à l'aide du résultat de la question précédente que le résultat du programme de calcul suivant est toujours égal à 1 Calcule p² pour les deux possibilités de p et interprète le résultat.

Les différents exercices que j'ai vu traités jusqu'à présent sur ce site ont toujours utilisé cette démarche lorsqu'on était en présence d'une suite d'éléments encadrés par deux termes tendant vers une même valeur. Mais, tu le sais, je n'ai jamais enseigné les maths, donc je ne peux pas garantir que c'est suffisant. Le problème est effectivement que ce n'est pas une suite monotone. D'habitude, on commence par montrer que la suite est croissante et majorée ou décroissante et minorée ce qu'on ne peut pas faire ici. Mais d'après ce que j'ai vu sur la toile, ceci n'est pas utile, la suite peut alterner, il suffit que ses valeurs restent toujours entre celles des deux suites prises en compte dans le théorème. Il faut peut-être attendre un avis plus autorisé que le mien.

Bonjour, Ne peut-on pas simplement utiliser le théorème des gendarmes ? Un est compris entre deux termes qui tendent vers 0.

Bonsoir, Juste une remarque : Les indices horaires donnent les déphasages entre les tensions homologues au prirmaire et au secondaire, donc, soit les tensions entre phases et neutre, réel ou fictif, soit les tensions composées. Les déphasages entre les tensions aux bornes des enroulements ne sont égaux à ceux donnés par l'indice horaire que pour des couplages identiques,. Cela n'explique donc pas a priori pourquoi on ne peut pas coupler un Yy6 avec un Dd10. Et si on prend un Yy0 et un Dd0 ? Mais je me demande s'il n'y a pas un problème lors de fonctionnements en déséquilibré, ce qui peut facilement exister pour des réseaux triphasés qui alimentent différents utilisateurs domestiques en monophasé.

Bonjour, Si c'est effectivement un pdf, le mieux est de le mettre en pièce jointe.

Bonsoir, Qu'as-tu fait jusqu'à présent

De rien, bonne continuation.

Voilà, mais il est bon quelquefois de relire l'énoncé pour voir ce qu'on cherche. Le point de départ est qu'on cherche l'ensemble Ek des points du plan tels que MA/MB=k. On commence par étudier le cas particulier k=1 qui risque de poser un problème pour la suite. On constate que E1 est la médiatrice du segment [AB]. Ce cas étant résolu, on admet dans tout ce qui qui suit que k≠1. Partant de là, on aboutit finalement à MD.ME=0 avec les points D et E appartenant à [AB] et parfaitement définis par les relations de la question 3. Ceci définit complètement les ensembles Ek, cf. conclusion de la question 4. La question 5 est simplement là pour voir comment se situent D et E sur le segment [AB]. N.B. : Ce n'est pas mon rôle, mais si je peux me permettre, tu ne sembles pas au top en ce qui concerne les maths. Éventuellement, tu peux dire à ton prof que, si tu as entièrement résolu l'exercice, c'est aussi grâce à une aide importante auxiliaire. Après, c'est à lui de voir s'il veut ou peut faire quelque chose pour toi.

Oui, effectivement, ça a un lien avec tout ce qui précède. Tu as montré que MA/MB=k équivaut à (MA-kMB)(MA+kMB)=0. Ensuite tu as montré que MA+kMB=(1+k)*MD MA-kMB=(1-k)*ME On exploite donc le fait que le produit des termes de gauche est nul, en écrivant que (1+k)*MD*(1-k)*ME=0 soit (1-k²)*MD.ME=0 en remplaçant la multiplication par le produit scalaire et comme k est différent de 1 tu en déduis...

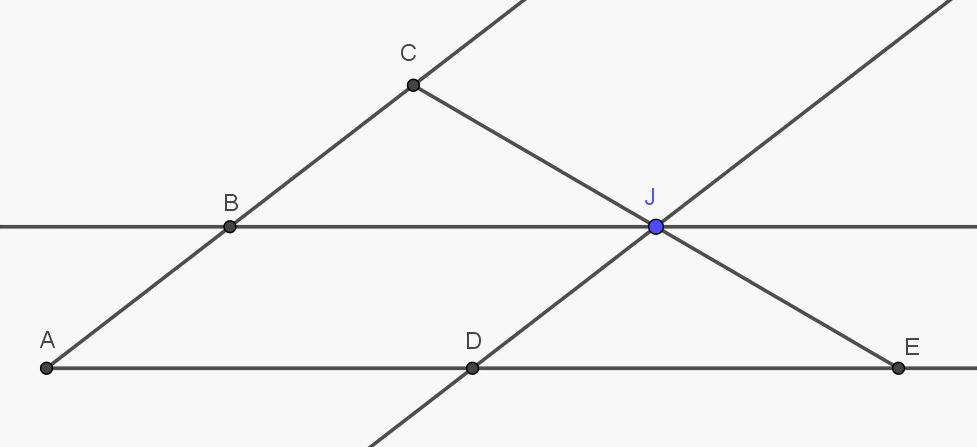
En interprétant le 2ème exercice ainsi : On cherche les deux points formant un segment dont J est le milieu (donc en particulier alignés avec J). Une construction possible est la suivante : On mène de J la parallèle à la première demi-droite qui coupe la deuxième en B. On trace le symétrique C de A par rapport B. On mène de J la parallèle à la deuxième demi-droite qui coupe la première en D On trace le symétrique E de A par rapport D. Vu Thalès, comme AB=BC et AD=DE, JC=JE et J est bien au milieu de C et E qui sont donc les emplacements des cachettes.

Bonjour, (1-k)BM passé à gauche devient -(1-k)BM, soit -BM+kBM et le -BM s'élimine avec celui qui y était déjà.

Il faut calculer les coefficients directeurs en comptant les carreaux. figure.ggb

Re-bonjour Denis, J'ai fait le tracé avec Geogebra à l'ordinateur. Même en plein écran, sur la figure complète, on ne voit pas l'écart. Il faut zoomer la partie centrale pour le voir. En fait, à mon avis, le seul moyen c'est de calculer les coefficients directeurs des éléments formant la diagonale et de voir qu'ils ne sont pas égaux.

Bonjour, C'est bien de là qu'il faut partir. Toujours avec ma notation de vecteurs... BA=(k+1)BD dont j'inverse tout de suite le k+1 en 1+k soit BA=(1+k)BD BA=BM+MA BD=BM+MD => BM+MA=(1+k)(BM+MD) soit, en passant (1+k)BM à gauche et en arrangeant un peu, MA-kBM=(1+k)MD d'où MA+kMB=(1+k)MD Pour la deuxième relation, la démarche est quasi la même.

Bonne soirée également.