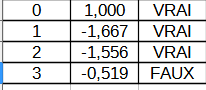julesx

Donc reviens à ça et trace correctement les points A,B et C compte tenu de ma remarque.

Lorsque tu reviendras, revois mon message précédent.

Mais les coordonnées de A sont(2,0), donc 2 en abscisse et 0 en ordonnée ! Et pour B et C, c'est faux. B abscisse -√2 ordonnée √2 C abscisse -√2 ordonnée -√2 Il n'y a aucune raison de passer par des angles, qui sont faux de toute façon. En fait, entre temps, j'ai compris ton erreur. Tu dois entrer les coordonnées cartésiennes séparées par une virgule, pas par un point-virgule. Le point-virgule fait croire à Geogebra que ce sont des coordonnées polaires, d'où les angles. Donc, revois le tracé en entrant A=(2,0) B=(-√2,√2) C=(-√2,-√2)

C'est pratiquement que de la géométrie. Fais les parties a) et b), par exemple avec Geogebra pour le a) et poste le tracé.

Bonjour, J'espère que c'est une erreur de transcription ! Black Jack a trouvé 2 comme module, Donc, ce n'est pas "également √2". De toute façon, comme z2 est le conjugué de z1, on a |z2|=|z1| =2. En ce qui concerne les arguments, une fois de plus, le cours te donne la méthode. On a cosθ=Réel(z)/|z| et sinθ=Imaginaire(z)/|z| Par contre, il est important de calculer les deux car l'argument n'est pas forcément compris entre 0 et π. Donc, comme ici, z1=-√2+i√2, on a cosθ=-√2/2 donc θ=±3π/4 sinθ=√2/2 Comme le sinus est positif, un argument de z1 est donc de 3π/4. On procède de même pour z2=-√2-i√2 cosθ=-√2/2 sinθ=-√2/2 Comme le sinus est négatif, un argument de z2 est donc de -3π/4. On peut évidemment retrouver directement ces valeurs à l'aide du cercle trigonométrique. On peut aussi noter que, comme les deux complexes sont conjugués, leurs arguments sont opposés. On peut aussi vérifier ces valeurs à l'aide de la transformations cartésienne-polaire de la calculette, mais sauf modèle spécial, elle ne retourne pas de valeur exacte en radians.

Voir la partie de cours "complexes et géométrie". Celle ci te dit en particulier Donc, à zA=3+i√(c-9) on associe le vecteur OA de coordonnées (3;√(c-9)) et à zB on associe le vecteur OB de coordonnées (3;-√(c-9))

Bonjour et bienvenue sur le site, Si ce n'est pas trop tard... Soit à montrer que P(n) : An=I3+nJ+n(n-1)/2*J² Initialisation Pour n=1, A1=A=I3+J P(1) est donc vraie. Hérédité Soit k un entier naturel positif. On suppose P(k) vraie. Montrons que P(k+1) est aussi vraie, c’est à dire que Ak+1=I3+(k+1)J+(k+1)k/2*J² Par hypothèse de récurrence Ak=I3+kJ+k(k-1)/2*J² Ak+1=Ak*A=Ak*(I3+J)=(I3+kJ+k(k-1)/2*J²)*(I3+J) Je te laisse développer et simplifier le produit pour arriver finalement à Ak+1=I3+(k+1)J+(k+1)k/2*J² On a donc P(k+1) vrai. P(n) est initialisé et héréditaire, donc elle est vraie pour tout entier naturel n. Si nécessaire, reviens pour des compléments.

Bonjour et bienvenue sur le site, De base, pour voir si une suite un est décroissante, on regarde si un+1-un est négatif. Ici un+1-un=(n+1)²/(n+1)!-n²/n! En mettant 1/n! en facteur, il vient un+1-un=1/n!*[(n+1)²/(n+1)-n²]=1/n!*(n+1-n²). Il ne reste plus qu'à trouver le signe du trinôme -n²+n+1 pour conclure.

Bonsoir Denis, Je n'avais pas pensé à la démarche inverse. Mais, comme de toute façon, je suis ignare en espagnol, je n'aurais rien pu apporter.

Bonsoir, Je ne maitrise malheureusement pas l'espagnol, comme ça semble être le cas de l'ensemble des intervenants de ce site. Il y en a peut-être eu initialement, mais là... Je ne sais pas si tu as entré ton texte dans un traducteur, à tout hasard je l'ai passé dans Deepl Traduction (car Google traduction avait des problèmes avec la "pierre à l'édifice" qu'il traduisait par "ma perte au bâtiment" !). Ce traducteur m'a retourné le texte suivant : Bonjour je suis José Rodriguez, j'ai 23 ans, je suis étudiant en biologie spécialisé en entomologie à l'Université Nationale Autonome de Mexico, en attendant la fin de mes études, je souhaite rejoindre l'association pour partager ma passion pour les sciences et les arthropodes et contribuer à la vie associative de la ville. Je partage les mêmes valeurs qui animent l'association : - la convivialité - l'entraide - la découverte - l'accès à la culture pour tous et - la lutte contre les discriminations, étant issue d'un milieu défavorisé cette problématique me concerne personnellement et je sais que l'accès à la connaissance peut être difficile en fin de compte. Ses ateliers du patrimoine attirent mon attention et j'aimerais pouvoir apporter ma pierre à l'édifice en proposant ma candidature pour être bénévole et permettre l'accès aux sciences pour les enfants et les adultes. Mes précédentes expériences en centre de loisirs et à l'école me permettent de me familiariser avec les ateliers ludiques et la facilité que j'ai à m'adresser au jeune public me permet d'apporter une expérience supplémentaire pour mon futur métier de professeur de biologie. Dans l'attente d'une réponse favorable à ma demande, je vous prie d'agréer mes meilleures salutations". Moi, je n'y vois rien à redire en ce qui concerne le fond. Désolé de ne pas pouvoir t'aider d'avantage, peut-être que cela aura pour mérite de réveiller un vrai expert.

Désolé, je ne suis pas suffisamment compétent dans ce domaine. Mais tu peux mettre ton travail en pièce jointe (à l'endroit, si possible). Un prof de maths y jettera peut-être un coup d’œil.

Non, il n'y a pas de courbe correspondant à h(x). Cette fonction permet simplement de trouver les positions respectives de la droite et de Cf.

Non, elle est au dessus ou en dessous, mais jamais tangente. Ci-joint un tracé partie de la partie concernée.

Le signe de h(x) est en lien avec la position respective de la courbe et de la droite : h(x)<0 => la droite d'équation y=x est en dessous de Cf h(x)>0 => la droite d'équation y=x est au dessus de Cf. Au point d'abscisse 0, Cf coupe la droite.

Bonjour, 1)b) Je suppose que tu as trouvé f'(x)=(2x²+1)*ex²-1. Tu as du voir en cours le lien entre le signe de la dérivée et le sens de variation de la fonction. Ici, 2²+1>0 sur R et ex²-1>0 sur R donc la dérivée est toujours positive. Il s'ensuit que f(x) est uniformément croissante sur R. 3) h(x)=x-x*ex²-1=x(1-ex²-1). D'après l'énoncé, 1-ex²-1≥0 sur [-1;1]. Donc le signe de h(x) est celui de x sur cet intervalle. A toi pour la suite et fin.

Alors, pourquoi avoir choisi l'option "mathématiques expertes" ? Il y avait surement mieux à faire (mathématiques complémentaires voire DGMEC). Mais comme c'est fait, arrête de parler de tes difficultés, ce qui ne changera strictement rien, et mets toi au travail. Demander des corrigés et les recopier ne servira qu'à faire croire à ton prof que tu maitrises le sujet alors que ce n'est pas le cas. Cela dit, il s'en rendra bien compte lors du premier contrôle.

S'imaginer qu'une méthode pas à pas fonctionne est une illusion. C'est ton illusion. Tu as déjà dit tout cela ! Tu as le droit de penser ce que tu veux mais n'oblige pas tout le monde à faire pareil.

Avec le très peu de demandes que nous avons actuellement, on ne peut pas trop faire le difficile. On ne peut que se réjouir lorsque un demandeur donne assidument suite, comme ça a été le cas de Mihawk7, Quant aux autres, tant pis pour nous ou pour eux s'ils se contentent d'une réponse fragmentaire. Et si la réponse est quasiment complète, pourquoi y aurait-il une réaction ? Si on veut un échange, il faut procéder pas à pas, mais je sais que tout le monde ne veut pas de ce type de démarche. Ceux qui l'utilisent ne se plaignent d'ailleurs pas de l'absence de réaction puisque la méthode ne la justifie pas. Ils pourraient éventuellement s'attendre à une formule de politesse finale, mais...

Bonjour, Pour moi, il faut que tu reprennes ce qui a été dit en cours à propos des congruences, en particulier des différentes propriétés. Par exemple, pour le 2)a), on sait que tout entier pair est congru à 0 modulo 2. Or, comme p et q sont entiers, pq² est un entier et 2pq² est un entier pair. Ensuite, pour compléter le tableau, tu dois utiliser les relations entre les congruences des termes des relations. Le but final est de voir dans la dernière ligne la cellule qui vérifie l'équation et pour celle-ci si elle est compatible avec les hypothèses de départ. (p et q premiers entre eux). En fait, ça revient à la démarche proposée par Black Jack, mais présentée autrement. Cela dit, je ne suis pas spécialiste, si un matheux veut prendre le relais, qu'il n'hésite pas.

Peut-être pas tout à fait, car ces valeurs sont fausses. U1=-2/3 U2= -2/9 U3= 25/27

Le tableau rempli avec un arrondi à 3 chiffres après la virgule. Essaie de comprendre comment on a fait. N.B.: Le programme Python ne donne que le dernier résultat. Si on les veut tous, il faut mettre le print(u) dans la boucle while. n=0 u=1 while n<3: u=u/3+n-2 n=n+1 print(u)

Tu ne pourrais pas mettre tes pièces jointes dans le bon sens ? En plus, pour des calculs aussi simples, l'écriture au clavier suffit ! Cela dit, je vois une erreur de signe -(280-40*0,85n)=-280+40*0,85n. Ensuite, 280-280=0 et on peut mettre 40*0,85n en facteur dans ce qui reste. Mais là, je me déconnecte. Merci aux autres intervenants de prendre le relais.

Essaie au moins de faire le 3)d) en calculant la différence. La suite est croissante si la différence est positive et décroissante si la différence est négative.

Bonjour, 3)d) Utilise la méthode classique consistant à chercher le signe de un+1-un. 4)a) Décompose ta somme en deux termes somme de 280 de 0 à n : le résultat est immédiat somme de 40*0,85^k de 0 à n : En mettant 40 en facteur, tu obtiens la somme de 0 à n des termes d'une suite géométrique de raison 0,85 et de premier termes 1. Poste tes résultats si tu veux qu'on vérifie.

Non, parce qu'il ne suffit pas de considérer un cas particulier. Regarde ici https://www.lelivrescolaire.fr/page/16683658