julesx

Bonjour et meilleurs vœux, Je ne pense pas que ce soit une bonne idée de forcer à être connecté pour accéder aux contenus des demandes et réponses. Ceci pour deux raisons, l'une que j'ai déjà évoquée, qui permet à de simples amateurs de se "cultiver", la deuxième, vœu pieux, qui est de donner envie, au vu des contenus, de se joindre à notre communauté. Il ne reste plus qu'à espérer que le site retrouve un peu de vitalité. C'est mon souhait pour 2024. Encore bonne année à tous.

Bonjour, Pour le premier exercice, un point de départ : On veut le résultat de 2015*(-h)17-2 sachant que 2015*(h)17-2=-2015. Or (-h)17=(-1)17*h17=-h17 puisque 17 est impair. Donc f(-h)=-2015*h17-2 où il n'y a plus qu'à remplacer 2015*h17 par sa valeur déduite de f(h)=-2015. Je te laisse terminer et poster le résultat que tu trouves

Bonjour, Je ne suis pas matheux, je bricole simplement, mais, en attendant mieux... En espérant avoir bien lu, je pars de x/(x²+1)*ln(cosh(x)-1). cosh(x)-1=2sinh²(x/2) Donc ln(cosh(x)-1)=ln(2sinh²(x/2))=ln(2)+2ln(sinh(x/2)) Quand x tend vers l'infini, sinh(x/2) se comporte comme (est équivalent à ?) ex/2/2. Au total, je te laisse vérifier que, compte tenu du fait que x/(x²+1) fait tendre vers 0 les termes constants restants, il ne subsiste que x/(x²+1)*x qui tend donc vers 1.

Il faut chercher sur quels intervalles f'(x) est positif et sur quels intervalles f'(x) est négatif. Comme f'(x) est un trinôme, on cherche ses racines et on utilise le fait que f'(x) est du signe du coefficient de x² à l'extérieur des racines et du signe contraire entre ces racines. Ensuite, tu dois savoir que f'(x)>0 => f(x) croît et que f'(x)<0 => f(x) décroît. C'est du cours . Tu fais cela et tu postes le tableau obtenu.?

Bonjour, Pourquoi serait-ce faux ? L'équation de la tangente est bien la même que celle qui apparait sur le tracé de PAVE (auquel, en passant,j'envoie mes meilleurs vœux). Donc ton équation de la dérivée est forcément juste. Par contre, c'est curieux que tu ne puisses plus de connecter avec ton ancien pseudo.

Bonjour, Merci pour le retour. A priori, donc, il ne fallait pas essayer de partir de P(x) sous la forme habituelle mais n'utiliser que la relation P(k)=k/(k+1). On obtient bien ainsi Q(x)=x.(x-1).(x-2)*(x-3) * ... * (x-n). Mais, sauf si quelque chose continue à m'échapper, si on essayait de retrouver P(x) à partir Q(x)=(x+1)*P(x)-x, on aurait du mal à trouver une forme de polynôme à cause du x+1 au dénominateur.

Bonsoir à tous, Comme il y a de moins en moins de clients, je butine en espion non connecté sur d'autres sites, histoire de quand même faire fonctionner mes méninges. Je suis tombé sur l'exercice ci-joint, trouvé sur l'ile aux maths, et vu que jusqu'à nouvel ordre, il n'y a pas de suivi, je me permets de le poster ici avec mes interrogations. Voilà mes problèmes : * Pour k de 0 à n, il y n+1 valeurs différentes de P(x), c'est possible, mais ça fait une valeur de trop si on voulait en déduire les coefficients de k. Ce n'est demandé ni forcément indispensable, mais pour k=0, cela entraine obligatoirement que le coefficient constant de P(x) est nul. A priori, cela devrait plutôt être de k=0 à n-1 ou k=1 à n, non ? * Le degré de Q est forcément n+1, donc Q a n+1 racines, dont les n premières valeurs de k utilisées au départ (k de 1 à n si on oublie k=0). Donc la factorisation jusque là est facile, par contre, il reste le terme en xn+1 et je ne vois pas comment trouver la racine correspondante. Une simulation avec un logiciel de calcul formel pour quelques polynômes ne me donne pas de solution interprétable. Compte tenu de ceci, je ne vois évidemment pas comment on peut calculer Q(n+1). Par contre P(n+1) s'en déduirait facilement. Si l'un d'entre vous a des idées... Cela dit, excellentes fêtes de fin d'année à tout le monde. Julesx

Bonjour volcano47, L'épaisseur du tuyau ne joue évidemment pas sur le débit. Il faut voir que les dimensions fournies par les constructeurs sont le diamètre extérieur et l'épaisseur du tuyau, je suppose que c'est ce qui importe à l’utilisateur, à cause de l'encombrement au moment de la pose. Pour le débit, évidemment ce qui compte, c'est le diamètre intérieur, qui se calcule par le diamètre extérieur moins deux fois l'épaisseur.

Bonsoir Black Jack. Le problème c'est qu'il faut voir à quoi correspondent ces dimensions. Ce sont des tuyaux circulaires, donc il ne s'agit pas de longueur et de largeur. Va faire un tour sur la toile, c'est bien expliqué à quoi elles correspondent.

Désolé, j'avais zappé le "seulement si". Revois le post de Black Jack.

.

Bonsoir Denis, Je pensais bien que ce n'était pas dans les cordes de notre administrateur, c'était plus un billet d'humeur qu'une vraie demande. Entre temps, j'ai consulté la liste des derniers visiteurs, on voit quels posts ont été regardés, mais ça s'arrête aux dernières 30(?) minutes donc il faudrait ne faire que ça si on voulait exercer un vrai contrôle. Cela dit, les demandes deviennent de plus en plus rares, donc il vaut mieux répondre, même si on sait qu'on aura peu de chances d'avoir un retour. Bon week-end prolongé.

Bonsoir, Je sais que c'est très agréable de lire des posts sur des sites sans être connecté, voire inscrit, j'en profite également. Le problème, c'est qu'en tant qu'intervenant, quand on poste une réponse et qu'il n'y a aucun retour ni même aucune trace de connexion du demandeur, on ne sait jamais si ce dernier en a pris connaissance. Je n'y connais rien en termes de gestion de site, mais il me semble quand même, vu ce que font les sites commerçants, qu'il doit y avoir moyen de tracer un peu les visiteurs. Bonne soirée.

Bonjour, 1) Les taux de compressions sont les inverses des gains de place. Par exemple, pour que le ficg=hier prenne 4,411 fois moins de place, il faut un taux de compression de 1/4,41 soit environ 0,227. 2) La démarche est la suivante : Calculer la taille initiale avant compression 5,76*11,025=63,5Mo Ramener cette valeur à celle pour une seconde 63,5*106/(3*60)=352800 octets Convertir en fréquence sachant qu'on échantillonne sur 8 bits 352800/8=44100 soit 44,1 kHz 3) La réponse se trouverait facilement sur internet : La compression MP3 est qualifiée de "destructive" car elle supprime les sons peu audibles. Elle ne permettrait donc pas de retrouver le signal avant compression (contrairement à d'autres types de conversions dites "non destructives" ou "sans pertes").

Bonsoir, Au moins deux visites mais sans réactions de ta part. Si tu attendais plus en termes de réponses, il fallait le dire.

Bonjour, Vu que les points A,I, et C sont alignés, que les points D, I et J sont alignés et que [AJ] est parallèle à [DC], tu peux appliquer Thalès aux triangles AIJ et DIC. Tu as donc AJ/DC=AI/IC=IJ/DI. Ceci te permet de répondre aux questions 1) et 2).

De rien, bonne continuation. (mais à l'avenir, essaie un peu de regarder ton cours avant de poster, c'est trop facile d'attendre qu'on te donne toutes les démarches alors que certaines se déduisent immédiatement de ce qui a été vu en classe ou de ce qui figure dans ton manuel).

OK, éventuellement, tu peux préciser que , comme le module de zI est √(2-√2) et que son argument est 3π/8, sa forme trigonométrique est ZI=√(2-√2)*(cos(3π/8)+isin(3π/8)

d) Ce que tu as fais n'est pas faux, mais ça n'est pas exactement dans l'optique de l'énoncé. On te demande de déduire les valeurs exactes de cos(3π/8) et de sin(3π/8) mais toi, tu déduis la valeur de θ=3π/8 alors que tu connais cette valeur. Pour moi, il faut partir des deux expressions de ZI ZI=(2-√2)/2+i√2/2 ZI=√(2-√2)*(cos(3π/8)+isin(3π/8) Par identification √(2-√2)*cos(3π/8=(2-√2)/2 => cos(3π/8)=√(2-√2)/2 √(2-√2)*sin(3π/8)=√2/2 => sin(3π/8)=√2/2/√(2-√2) qu'on peut transformer en sin(3π/8)=√(2+√2)/2 moyennant quelques petits calculs.

Bonjour, OK pour l'affixe et le module de ZI, mais garde la valeur exacte √(2-√2)

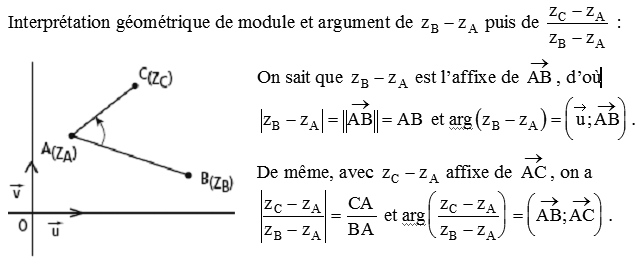
Pour info avant de continuer, un petit document dans le cas général Pour la suite, c'est du calcul, tu sais que I est le milieu de AB, donc que zI=(zA+zB)/2. Il n'y a plus qu'à...

Je t'ai expliqué précédemment ceci : Donc, comme z1 a pour argument 3pi/4, l'angle entre les vecteurs u et OB vaut également 3pi/4

Tu as compris pourquoi entre temps ?

OI est la médiane du triangle OAB issue de A. Mais comme ce triangle est isocèle, cette médiane est aussi la bissectrice de l'angle de sommet A. L'angle (u;OI) est donc la moitié de l'angle (u;OB) et l'angle(u;OB) est l'argument du complexe z1 que tu as calculé précédemment. Je te laisse en déduire la valeur de (u;OI)

C'est bien ça. Continue