julesx

Bonjour, Je ne te donne à chaque fois que des indications. A toi de les utiliser et de poster éventuellement les résultats trouvés. Exercice 14 1) Il suffit de regarder le graphique. 2) Ça s'explique par la variation de l'angle que fait la direction des rayons solaires avec l'axe vertical des panneaux solaires. 3) Pradiative=Pmax/0,2 avec Pmax lu sur le graphique. 4) Il suffit de diviser Pradiative par 3700. Exercice 15 1) Il suffit de lire le tableau. 2) A Blaye, les rayons du soleil frappent le sol avec un angle de 45°. Pour que les panneaux solaires les reçoivent perpendiculairement, il faut que ces panneaux fassent eux-même un ange de 45 ° avec le sol (fais éventuellement une petite figure). Exercice 17 1) Là encore, il suffit de lire le tableau puis d'utiliser la relation. 2) Tu divises l'écart par la valeur théorique en convertissant éventuellement le résultat en %.

De toute façon, la demanderesse a abandonné. Malgré l'intérêt qu'il peut présenter, le mieux serait de mettre cette demande à la corbeille sauf si quelqu'un s'y intéresse et poste un début de réponse. Dans ce cas, certains d'entre-nous peuvent y donner suite. A noter que la plupart des réponses peuvent se trouver sur la toile.

Bonsoir, Juste une petite incursion, mais je ne m'incruste pas. Si maïkamascary n'a pas la calculette numworks, il y a un émulateur en ligne à cette adresse https://www.numworks.com/fr/simulateur/ c'est peut-être de cela que voulait parler l'auteur de l'énoncé. En tout cas, voilà ce qu'on obtient avec la bonne configuration de l'écran graphique .

De rien, à une autre fois, peut-être.

Tu as oublié que c'est une équation produit ! R-3=0 donne R=3 cm qui convient aussi. Par contre -5,65 ne convient pas puisqu'il s'agit d'un rayon, qui est forcément positif. En résume, il y a deux possibilités, R=2,65 cm et R=3 cm.

Oui, bien sur.

Oui pour Ve+Vb=60π+(4/3)π×R³ =Non pour 128πR, le volume total pour le schéma 2 vaut π4²*2R=32πR Après simplification par π, il vient bien (4/3)R³-32R+60=0. Ensuite, pour aboutir à la relation de l'énoncé, il faut multiplier le membre de gauche par 3/4 3/4*((4/3)R³-32R+60)=R³-24R+45. Il reste à vérifier que R³-24R+45=(R-3)(R²+3R-15) en développant le membre de droite puis à résoudre l'équation produit (R-3)(R²+3R-15)=0.

Qu'as-tu trouvé pour la somme à la question 2 ? En notant alors V le volume total pour le schéma 2, tu écris que Ve+Vb=V avec V volume du cylindre dont le diamètre de la base est de 8cm et dont la hauteur est de 2R. Ceci va te donner une équation qui après simplification, te donne le résultat fourni à la question 3.

Bonsoir, C'est quoi Tema ? Il faut se relire avant de poster ! Cela dit : Tu sais calculer le volume d'un cylindre, sinon tu vas chercher son expression sur Internet. Tu sais calculer le volume d'une sphère , sinon tu vas chercher son expression sur Internet. Tu sais faire une addition. Partant de là, tu dois aboutir à la relation fournie dans l'énoncé. Donc, moi, j'attends le résultat de ton travail jusque là.

C'était au cas où, mais, évidemment, si tu ne postes pas au minimum l'énoncé, je ne vois pas ce qu'on peut faire d'autre pour toi.

Merci, Tous mes meilleurs vœux également.

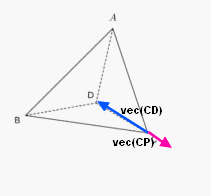
Bonjour, Le vecteur CP est en sens opposé du vecteur CD et sa norme est la moitié de celle de CD, donc égale à 1,05 cm sur la figure. Voir pièce jointe où les dimensions ne sont pas exactement respectées. PS. : Je ne comprends pas ta figure. M est sur le segment AB au 2/3 à partir de A, N est sur le segment AC au 3/4 à partir de A et Q sur le segment AD à la moitié en partant de A.

Bonjour volcano, Malheureusement, si ! SSI est bien la spécialité sciences de l'ingénieur.

A ce que je vois, tu ne veux même pas faire l'effort de répondre à la question Q0. Tant pis, "pas de bras, pas de chocolat" 😕

Bonsoir, Deux semaines alors que tu n'as même réussi à faire la question Q0 ? C'est du français, pas de la physique, et si tu ne comprends pas certains termes, il existe des dictionnaires et Internet.

Bonsoir, Avec ce début d'énoncé, il est évident que personne ne peut t'aider. Mais, sauf coïncidence malheureuse, la phrase est le commencement du sujet traité ici : https://www.e-bahut.com/topic/46056-polynôme-du-second-degré/

Petite rectification : En fait, on obtient un système de 3 équations à deux inconnues. On en choisit 2 pour la résolution et on contrôle que le couple α et β obtenu vérifie la 3ème.

C'est bien ça. Éventuellement, tu peux vérifier en traçant la courbe correspondante avec ta calculette ou un logiciel sur ton ordinateur. Bonne soirée.

Le système est constitué par les relations que tu as trouvées sur le tracé. 5= 4a + 2b + 1 1 = 4a+ b (car f'(2)=1 coefficient directeur de la tangente) 1=c Tu as donc bien trois équations à 3 inconnues avec, en fait, déjà une partie résolue, puisque c=1.

C'est ça. Tu ne devrais pas avoir besoin de demander confirmation. Il n'y a plus qu'a trouver a et b.

Non, à l'origine, x=0 ! Sachant que f(x)=ax²+bx+c. Donc la 3ème équation est ?

Black Jack a dit "3 équations" ! Tu n'en a écrit que 2.

Il faut trouver α et β tels que vec(MQ)=α*vec(MN)+β*vec(MP). Pour faire cela, tu remplaces à gauche vec(MQ) par son expression en fonction des vecteurs de la base à droite vec(MN) et vec(MP) par leurs expressions en fonction des vecteurs de la base et tu regroupes les coefficients de ces vecteurs. C'est là que tu obtiens un système de deux équations à deux variables α et β. Si ce système a une solution, tu as bien obtenu le fait que vec(MQ) est une combinaison linéaire de vec(MP) et vect(MN), donc que Q appartient au plan MNP.

Non, il faut garder les vecteurs de la base (AB,AC AD). Tu ne vois pas que tes relations sont fausses ? Tu as trois vecteurs que tu identifies à trois réels !

Quel autre ordre ? Il faut montrer que Q appartient au plan MNP, la bonne méthode est celle suggérée par l'énoncé. Reprends les 3 relations que je t'ai postées et regarde si tu arrives à une relation du type vec(MQ)=α*vec(MN)+β*vec(MP).