julesx

Bon, écoute, je te joins le script complet pour cette partie, essaie de voir ce que tu peux en tirer. n=13 hauteur=0 duree=1 print(n) while n>1: if n%2==0: n=n//2 else: n=3*n+1; duree=duree+1 if n>hauteur: hauteur=n print(n) print("duree ",duree) print("hauteur ",hauteur) Rappels : n=13 pour tester le script hauteur=0 pour déclarer et initialiser la variable duree=1 idem et 1 car le premier nombre n'est pas compté ensuite. Partant de là, essaie de voir la suite. Par contre, je ne reste pas connecté, pour la suite, il faudra compter sur un autre intervenant.

C'est juste au cas où tu voudrais teste le script. Oui, mais il faut les initialiser, par exemple hauteur=0 et durée=1.

En respectant les indentations, en remplaçant n=n/2 par n=n//2 pour ne travailler qu'avec des entiers et en corrigeant le pint en print, on a while n>1: if n%2==0: n=n//2 else: n=3*n+1; print(n) Mais si tu veux vérifier avec le n=13 initial, il faut rajouter au début les deux lignes n=13 print(n) sinon le 13 de départ n'est pas affiché.

Attention cependant, if et else en minuscules, cf. la suite de l'énoncé à la question 5.

Bonsoir, Pour ce soir, ce sera bref. Si tu n'as pas avancé ou si personne n'a répondu d'ici demain, je reprendrai ce fil. 1) Il suffit d'appliquer la démarche. 13 impair -> 13*3+1=40 40 pair -> 40/2=20 20 pair -> 20/10=10 10 pair -> 10/2=5 5 impair -> 3*5+1=16 16 pair -> 16/2=8 8 pair -> 8/2=4 4 pair -> 4/2=2 2 pair -> 2/2=1 Terminé ! Le vol de 13 est donc 13 40 20 10 5 16 8 4 2 1 d'où sa durée est de 10 (10 nombres) sa hauteur est de 40 (maximum obtenu) 2) L'algorithme doit traduire la suite des opérations faites ci-dessus. Tant que n>1 Si n pair n <- n/2 Sinon faire n <- 3*n+1 Afficher n Fin si Fin Tant que 3) n%2 reste de la division entière de n par 2 (si n%2=0 alors n est pair) n//2 quotient de la division entière de n par 2 Partant de là, je te laisse coder l'algorithme en Pyrhon. A demain si nécessaire.

Bonjour, La réponse à la deuxième question fait allusion à l'étude de la fonction exponentielle, mais tu n'en as pas besoin ici. Utilise le résultat que tu connais, en remplaçant a et b par les valeurs numériques de l'énoncé.

d s'élimine dans le rapport Fe/Fg puisque c'est la même distance qui intervient dans les deux formules.

Bonjour et bienvenue sur le site, Un script pour la première partie, je l'ai testé. from random import randint tortue=0 lievre=0 while tortue<6 and lievre!=6: de=randint(1,6) if de==6: lievre=6 texte="Le lievre a gagne" else: tortue=tortue+1 if tortue==6: texte="La tortue a gagne" print(texte) Essaie plusieurs coups puis cherche comment le modifier pour répondre à la question suivante.

Bonjour, Pourquoi tu crées un nouveau fil ? Si tu n'as pas compris quelque chose aux réponses données dans le précédent, ajoute un message à la suite en disant ce qui t'arrête. N.B. : Dans la démarche pour le f) que je suggérai, je n'avais pas fait attention au fait que tu avais déjà démontré l'inégalité. Il suffit donc de faire la somme de 1 à n de la relation trouvée au e).

Bonsoir PAVE, A l'ile Maurice, il est actuellement 23h15. Il y a de fortes chances que Lilou ne réponde pas ce soir. Demain peut-être, on peut toujours espérer.

@anip2 Tu postes beaucoup, tu vas voir souvent, mais tu ne te manifestes que rarement. Du coup, on se demande ce que tu retires de nos réponses. A tout hasard, pour la question f), moi je ne serais pas parti dans une démonstration par récurrence. En plus, ton initialisation n'est pas juste. Pour n=1, n²/(n²+1)=1/2 et S1=1/2. La relation est bien vérifiée mais pas comme tu l'as écrite. Mois, je commencerais par justifier que n/(n²+n)<=n/(n²+k)<=1/n et je ferais la somme de 1 à n.

Une remarque à propos des questions b) et c) : Le range de i n'est pas juste, range (n) signifie que i commence à 0 et se termine à n-1. Pour les grandes valeurs, ça ne change pas grand chose, mais si on essaie S(1), S(2) et S(3) avec range(n), on voit tout de suite le problème. Le "bon" range est (1,n+1) A noter également que S(100)=0,995 arrondi au millième. S(1000) est bien égal à 0,999 avec le même arrondi par contre S(10000)=1,000.

Bonjour et bienvenue sur le site, Ça n'a pourtant rien d'insurmontable. 1) Il suffit de regarder les tracés. Les courbes semblent se couper pour x=1 (ce qu'on demande de démontrer à la question 2). Pour x<1, Cg est au-dessus de Cf. Pour x>1, Cf est au-dessus de Cg. 2) A l'intersection, x vérifie l'équation f(x)=g(x) soit e2x=e-x. Tu essaies de la résoudre ? 3) d(x)=e2x-e-x. Met e-x en facteur pour obtenir l'expression donnée dans la question a). Regarde déjà tout cela et reviens.

Si on veut être un poil moins fainéant, on peut raisonner ainsi : Dans la mesure où il y a deux "vrais" de suite, il faut que, dans la liste, il y ait deux fois de suite le même prénom. Comme, actuellement, ce n'est pas le cas, le bon prénom ne peut que se trouver en tête ou en queue de liste, donc qu'on ait une des deux combinaisons suivantes : Matt, Matt, Bob, Matt, Bob, John, Bob Matt, Bob, Matt, Bob, John, Bob, Bob Il ne reste plus qu'à voir laquelle des deux est compatible avec la suite lu ma me je ve sa di lu ma me je ve sa di ? M ? V V ? ? ? M ? V V ? ? (M pour mensonge, V pour vérité) sachant que la liste ne peut que commencer un vendredi ou se terminer un jeudi. Ça revient à la méthode de Denis, sauf qu'il n'y a que deux possibilités de positions de la colonne et qu'on est un peu plus proche de la demande formulée dans l'énoncé. Reste à savoir si le demandeur reviendra voir les réponses

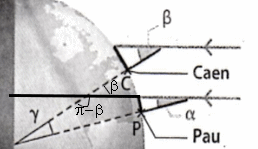
Bonsoir, Tu es en première donc tu connais la notion de tangente. En reprenant la figure tracée précédemment tu vois que tu as deux triangles rectangles. Dans chacun des deux, tu as la tangente de l'angle égale à la longueur au sol divisées par la hauteur du bâton. Exemple pour Caen : longueur au sol 38 cm longueur du bâton 1 m = 100 cm donc tan(β)=38/100 soit β=20,8°. Il n'y a plus qu'à faire pareil pour α.

Sauf si je ne vois pas clair, il n'y a pas d'erreur à la 3ème ligne. Par contre, ce qui me chiffonne depuis le début, c'est ce "12=" !

Ça a failli être bon ! Le problème, c'est que tu ne retrouves pas ton résultat initial parce que : (3-5x)²=(3-5x)(3-5x) et que,si tu mets 3-5x en facteur, les signes de 2x et de (3-5x) ne changent pas. Moi, pour minimiser le problème des signes, j'aurais mis 5x+3 en facteur. Ci-joint ma démarche, car je me déconnecte b=(5x-3)(x+1)+6x-10x²+(3-5x)² étalement b=(5x-3)(x+1)+2x(3-5x)+(3-5x)(3-5x) termes communs (on prend 5x-3 en changeant les signes nécessaires) b=(5x-3)(x+1)-2x(5x-3)+(5x-3)(5x-3) mise en facteur du terme commun b=(5x-3)[(x+1)-2x+(5x-3)] simplification b=(5x-3)(4x-2) mise en facteur du 2 b=2(5x-3)(2x-1)

OK pour les 68 VA, mais ton cahier des charges dit cosφ=0,5, pas 0,8. Mais ça ne change rien à la puissance nominale car 68 à 0,5 est compris entre 51 et 87, donc tu es obligé de prendre la valeur la plus élevée, soit 63 VA. Partant de là : au primaire I=63/400=0,16 A au secondaire I=63/24=2,63 A

Bonjour, Tu devrais quand même voir que tes résultats ne concordent pas avec ceux que tu as trouvés tout au début et qui, eux, sont justes. Tes erreurs dans ta méthode actuelle viennent du fait que tes mises en facteur sont fausses. Je reprends le a : a=9x2+12x+4-2x*(3x+2)+(4-9x2) La première chose à faire est d'<<étaler>> le plus possible les différentes termes a=(3x+2)²-2x(3x+2)+(2-3x)(2+3x)=(3x+2)(3x+2)-2x(3x+2)+(2-3x)(2+3x) ensuite, faire apparaître le terme commun au 3 a=(3x+2)(3x+2)-2x(3x+2)+(2-3x)(2+3x) mettre ce terme commun en facteur en le supprimant devant tous les autres a=(3x+2)[(3x+2)-2x+(2-3x)] il ne reste plus qu'à simplifier la partie de droite a=(3x+2)(3x+2-2x+2-3x)=(3x+2)(4-2x) et mettre en facteur 2 ou -2 si tu préfère que tous les coefficients de x soient positifs. Essaie de faire pareil avec b.

Bonjour, A propos des voyants, le cahier des charges dit : Comme il n'y a qu'un seul moteur, on n'a bien affaire qu'à 4 voyants. Si on oublie le problème du défaut moteur, il n'y a effectivement que 2 voyants allumés simultanément. Mais quid de la signalisation du défaut moteur ? Quel défaut veut-on détecter (blocage, coupure de phase, surchauffe..) et comment le détecter ? En ce qui concerne le câblage des voyants, la question qu'on peut se poser est ce qu'on veut signaler : l'alimentation de la bobine ou la fermeture du conttacteur.

Oui, c'est bon, sauf que tu aurais pu mettre 2 en facteur du deuxième membre : (x-4)(4x-10)=(x-4)*2(2x-5)=2(x-4)(2x-5).

Bonsoir, Trouvé sur la toile, si ça peut aider. N.B. : Le transfo 24 V est alimenté en 400 V au primaire, mais le cahier des charges ne l'interdit pas. De toute façon, l'armoire est supposée alimentée en 3x400 V, donc sans neutre accessible, donc tu ne peux pas faire autrement sauf à rajouter un transfo supplémentaire 400 V / 230 V. A noter que la remarque de Black Jack à propose de la simultanéité des fermetures des contacteurs s'applique aussi aux voyants, mais là, vu le 1 VA de chaque, on pouvait l'ignorer. C'est plus pour le principe...

OK, ça devrait aller d'autant pus qu'on te donne le résultat à trouver à la question 2)c).

Oui pour la raison, mais pas pour v0. vn=(un-1)/(un+4) => v0=(u0-1)/(u0+4) avec u0=1/2. Il suffit de calculer la fraction mais garde le résultat exact sous forme de fraction à cause de la suite.

Ce n'est pas la fonction mais la suite, mais à ce détail près, c'est ce que nous pensons...