julesx

Voir le forum "Discussion libre !". J'ai envoyé un MP à zola2.

Bonsoir volcano, Là, tu vas un peu trop vite que la musique, caliméro n'a même pas encore validé les réponses de PAVE à la partie A. Sur un autre site, on te dirait de respecter une charte qui veut qu'on n'intervienne pas tant que ce n'est pas absolument nécessaire (ce qui n'est pas le cas ici) lorsque un autre intervenant a commencé à répondre.

Bonjour PAVE, J'avais fait une réponse laconique, chacun ses méthodes. Je te laisse continuer, (si calimero veut bien se manifester). En ce qui concerne l'énoncé joint, moi, je préfère le pdf. En "splitant" l'écran, j'ai simultanément mes réponse et l'énoncé. Mais, là encore, chacun ses méthodes.

Bonjour, Comme tu as commencé, poste ce que tu as fait puis dis ce qui t'arrête.

Ce que tu veux montrer, c'est que 1-vk+1≤(1/2)k+1. Tu sais que Pk=>1-vk≤(1/2)k et que 1-vk+1=2/(4+vk)*(1-vk). Donc, si tu montres que 2/(4+vk)≤1/2, par produit avec l'autre relation, tu as bien 1-vk+1≤(1/2)k+1. Or, comme vk est positif , vk+4≥4 donc 2/(vk+4)≤2/4 soit 2/(vk+4)≤1/2. 1-vk≤(1/2)k 2/(vk+4)≤1/2 => 2/(vk+4)*(1-vk)≤1/2*(1/2)k OK ?

Bonjour, L'idée est effectivement d'utiliser les questions précédentes. Tu pars de 1-vk≤(1/2)k. D'après le a), tu as 1-vk+1=2/(4+vk)*(1-vk). Il suffit alors de montrer que 2/(4+vk)≤1/2. Je te laisse faire ?

Après ces échanges surement très intéressants pour les intervenants, on en est toujours au même point. leptitmateux vient voir si on a enfin posté des corrigés in-extenso des énoncés qu'il a posté. Comme ce n'est pas le cas, il ne voit pas pourquoi il se manifesterait. Désolé pour ce mouvement d'humeur !

J'ai vu que tu étais revenu faire un tour sur le site. Mais sans un minimum de contribution de ta part, personne ne te répondra. Aucun des exercices n'est insurmontable au départ, on demande simplement quelques calculs que même une calculette 4 opérations est capable de faire. A bon entendeur, salut !

Bonjour, Qu'est-ce que tu ne comprends pas ? La construction des losanges ?

Il vaut toujours mieux initialiser les variables que tu utilises. En principe, les logiciels actuels les mettent à zéro mais on ne sait jamais. Il y a cependant deux cas de figure : * Tu utilises ta variable au sein du programme avec une affectation, genre n=1 ou autre. Dans ce cas, l'initialisation est inutile, elle se fait au moment de la première affectation. * Tu utilises ta variable dans une boucle genre while ou for n=n+1. Dans ce cas, il vaut mieux l'initialiser car tu ne sais pas comment le logiciel traite la valeur initiale. Bonne continuation.

Comme le message d'erreur l'indique, il y a des problèmes d'indentation. En plus, tu n'as pas initialisé n. Ça doit se présenter ainsi

Pas de distinction entre quoi et quoi ? Ton script est correct sauf que, comme on cherche une durée supérieure ou égale à 200 la condition est while duree(n)<200. Cela dit, ça ne change rien au résultat, c'est pour le principe.

@ Eleor : Ton script ne va pas du tout. Tu désignes deux choses différentes par la variable n. Il faut distinguer le nombre n de la durée du vol. Appelle par exemple cette durée d. Partant de là, initialise n et d puis utilise le while.

Oui, l'entier ayant le plus long vol est 871 et la durée de vol correspondante est 179. Et, bien sûr, tu n'as pas besoin de rajouter les 3 lignes.

Bonjour, J'avais vu que c'était à rendre pour hier mais j'avais quand même essayé. Pour info, je ne sais pas si tu as regardé d'un peu plus près la notion de carré magique. En fait, on en trouve qui ne sont pas constitués des n² premiers nombres. Dans ce cas, les 4 premiers contrôles ne détectent pas d'erreur. Seul le dernier retourne False. Par contre, ici, l'énoncé spécifiait bien "tous les entiers de 1 à n²" d'où la nécessité du 5ème contrôle.

Bonjour, Si, j'ai essayé avec ton script. Mais print("vol ",vol(nmax)) affiche tous les nombres de vol, soit 179, ça fait peut-être beaucoup pour trinket. Non, pas forcément, tu as essentiellement besoin de vol(n) appelé par duree(n). Ensuite, il suffit de partir de n=1 et d'incrémenter n en appelant durre(n) jusqu'à ce que tu obtiennes une durée supérieure ou égale à 200. Le mieux, c'est d'employer while.

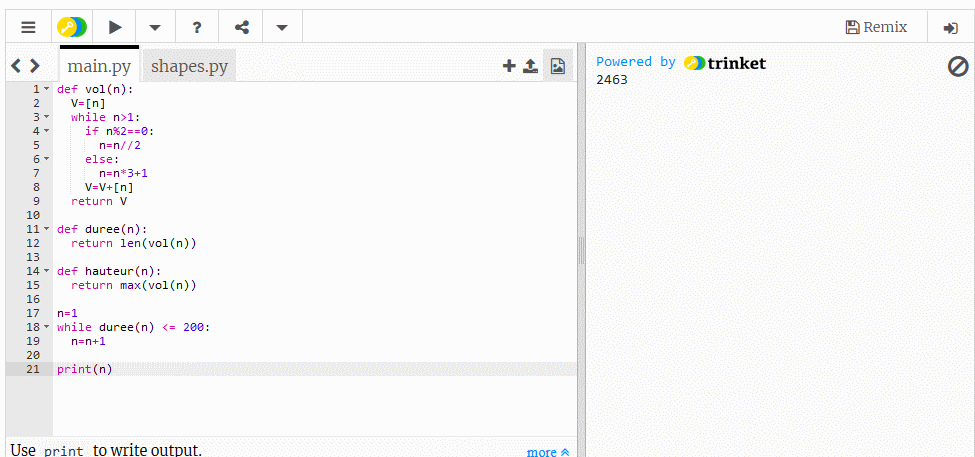
Je ne comprends pas non plus ton problème. Moi, quand j'ouvre trinket.io j'ai ça Je clique ici et le résultat s'affiche à droite, soit 703. Mais j'ai main.py et shapes.py en grisé alors que toi, tu as d'autres indications

C'est normal, tu n'as pas initialisé hmax. En plus, je ne suis pas à l'abri d'une faute de frappe. J'ai oublié de corriger un i malencontreux. Mais tu es aussi censée vérifier les scripts avant de le copier coller bêtement d'autant plus que j'ai laissé passé un oubli de nmax. Donc, je reprends, le bon script est def vol(n): V=[n] while n>1: if n%2==0: n=n//2 else: n=n*3+1 V=V+[n] return V def duree(n): return len(vol(n)) def hauteur(n): return max(vol(n)) hmax=0 nmax=0 for n in range (1,1001): h=hauteur(n) if h>hmax : hmax=h nmax=n print(nmax) N.B. : Il est évident qu'il faut rajouter en tête les fonctions auxquelles tu va faire appel. Python ne connait que ce qu'il y a dans le script ou ce qui est dans sa bibliothèque. Ce que tu crées n'existe que dans le script actuel ( sauf à créer un module, mais ça dépasse largement ce qu'on peut attendre à ton niveau).

OK, contente toi de print(n). Pour trinket.io, une fois que tu as copié le programme, tu cliques dans le petit triangle noir au dessus.Mais copie bien l'ensemble, avc les deux fonctions vol(n) et hauteur(n). Là, je me déconnecte pour le moment.

Il faut être un peu plus loquace ! Fais une phrase pour dire ce que tu imprimes. Tu peux aussi imprimer la hauteur correspondante.

Si tu mets ces instructions à la suite des fonctions, il suffit d'appeler hauteur(n) et de stocker le résultat dans une variable auxiliaire, par exemple h : for n in range (1,1001): h=hauteur(n) if h>hmax : hmax=h nmax=i N.B.: Pour le range, il faut ajouter 1 à la fin, c'est Python qui veut ça.

Il n'y a aucun calcul à faire, seulement créer l'algorithme qui affiche l'entier inférieur à 1000 ayant la plus grande hauteur (en se limitant pour le moment à celui-ci). Pour faire cela, tu as à ta disposition les fonctions définies précédemment, en particulier la fonction hauteur(n). Il faut évidemment afficher à fin deux éléments, l'entier et la hauteur. Donc tu commences par définir deux variables, nmax et hmax, que tu initialises à 0. Ensuite, tu fais varier n de 1 à 1000 en utilisant la fonction hauteur(n). Je te laisse continuer la réflexion.

Tout simplement en faisant appel à la fonction vol(n). Cf. question 5, tu dois avoir def vol(n): V=[n] while n>1: if n%2==0: n=n//2 else: n=n*3+1 V=V+[n] return V donc il suffit de rajouter en-dessous def duree(n): return len(vol(n)) def hauteur(n): return max(vol(n))

Bonjour, Au cas où ce n'est pas trop tard, pour "Vérification tous les chiffres entre 1 et n^2", je n'ai pas trouvé mieux que de balayer tous les nombres et de vérifier qu'ils sont dans le carré. Par contre, pour simplifier l'utilisation de "in", j'ai transformé la liste de listes en une liste simple. carre1=sum(carre,[]) for i in range(1,n**2+1): if i not in carre1 : magic=False

Bonsoir, Au cas où, une ébauche pour les deux conditions suivantes, mais sans garantie, donc à étudier et à tester. carre1=[[4,9,2], [3,5,7], [8,1,6]] carre=[[1,2,3], [4,5,6], [7,8,9]] n=len(carre) s=n*(n**2+1)/2 magic=True for ligne in carre : som=0 for col in ligne : som+=col if som !=s : magic=False for col in range(n): som=0 for lig in range(n): som+=carre[lig][col] if som !=s : magic=False som=0 for i in range(n): som+=carre[i][i] if som !=s : magic=False som=0 for i in reversed(range(n)): som+=carre[i][i] if som !=s : magic=False if magic : print("c'est un \"carré magique\"") else : print("ce n'est pas un \"carré magique\"") Il y a deux carrés au départ, un bon et un mauvais. Il suffit de changer carre1 en carre et carre en carre1 pour les tests.