Black Jack

Bonjour, Pour info (hors exercice) Remarque pleinement justifiée de jules sur "l'oubli" de la force de frottement de l'air sur les grêlons pendant leur chute dans le texte proposé. Voir par exemple ici : https://www.anelfa.asso.fr/Croissance-des-grelons.html Je fais quelques calculs pour vérifier ces données. Soit d (en m) le diamètre d'un grêlon, son volume est V = 4/3 * Pi * (d/2)³ = Pi * d³/6 Sa masse est m = 900 * Pi*d³/6 (avec rho glace = 900 kg/m³) m = 471*d³ La force de traînée aérodynamique est F = 1/2 * Rho(air) * S * Cx * v² = 1/2 * 1,29 * Pi * (d/2)² * 0,45 * v² = 0,228 * d²*v² La vitesse de chute est stabilisée lorsque La force de traînée aérodynamique compense le poids du grêlon, donc lorsque : 0,228 * d²*v² = 9,81 * 471*d³ v² = 20265 * d v = 142 * sqrt(d) Avec d en m et v en m/s Groupement des résultats : masse grêlon : m = 471*d³ vitesse stabilisée de chute : v = 142 * sqrt(d) Energie cinétique à l'arrivée au sol (si vitesse limite atteinte) : E = 1/2 * 471*d³ * 142² * d = 4748622* d^4 Exemple numérique : si d = 40.10^-3 m (40 mm) m = 471 * (40.10^-3)³ = 0,0301 kg (30,1 g) v limite = 142 * sqrt(40.10^-3) = 28,4 m/s (si distance de chute suffisante) E cinét = 4748622* (40.10^-3)^4 = 12,2 J ... valeurs qui correspondent raisonnablement avec celles données dans le lien. *************** Les vitesses limites de chute des grêlons varient très fort avec la taille des grêlons ... Les calculs de vitesse en négligeant les effets de la force de frottement des grêlons dans l'air s'éloignent de très loin de la réalité. Je fais grâce des calculs pour trouver la distance parcourue en fonction de la vitesse ... Voila par exemple ce que cela donne pour les grêlons de 40 mm de diamètre. On voit qu'on approche raisonnablement la vitesse limite de chute après une distance de chute relativement petite ... qui pousse à considérer que la vitesse limite est, le plus souvent, celle d'arrivée au sol des grêlons (compte non tenu évidemment des effets éventuels du vent ou des courant d'air ascendant). **************** Ceci est évidemment hors exercice, mais je pense (à tort ou à raison) qu'il est parfois intéressant de resituer les problèmes dans le concret et pas dans le cadre d'exercices d'école où on a négligé (comme trop souvent) des effets qui ne sont pas du tout négligeables et qui donnent un tout mauvais ressenti aux élèves des réalités physiques.

Bonjour, Pour moi, il faut être plus précis pour les questions 3. On ne doit pas utiliser le calcul intégral mais rien n'interdit d'utiliser sa calculette, tout est en place pour le faire : 3a : s5 = 0,2/1,2 + 0,2/1,4 + 0,2/1,6 + 0,2/1,8 + 0,2/2 = 0,6456... 3b S5 = 0,2/1 + 0,2/1,2 + 0,2/1,4 + 0,2/1,6 + 0,2/1,8 = 0,7456... Et donc 0,6456 < A < 0,7456...

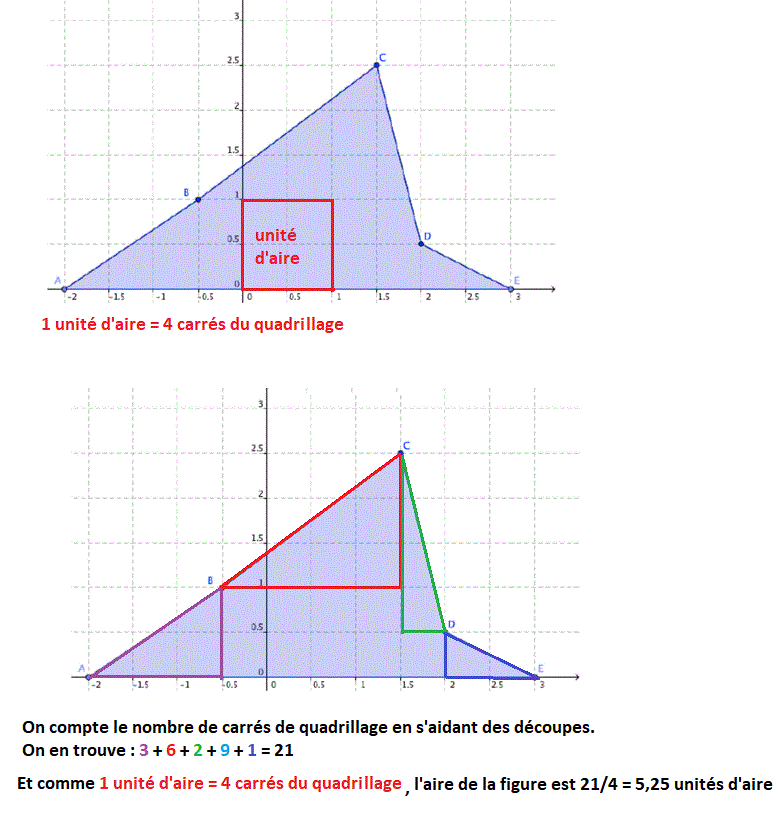
Bonjour, "Faut-il prendre le carré A= 0,25 unités d'aires Ou bien faut-il utiliser le rectangle A = 0,5 unités d'aires ?" Ni l'un ni l'autre, l'unité d'aire est une aire de valeur 1. Je fais l'exercice 2 pour montrer :

Bonjour, Si rho = 1,3.10^-6 ohm.m (comme indiqué dans le lien donné par Denis CAMUS), alors : R = 1,3.10^-6 * 1500/(Pi*0,006²) = 17,24 ohms Energie sur 24 h = 17,24 * 0,2² * 24 = 16,6 Wh ***** Par contre, la valeur de rho = 1,3.10^-6 ohm.m est trop grande avec ce qu'on trouve en pratique.

Bonjour, Sauf distraction de ma part, il y a des erreurs dans les dérivées dans plusieurs des messages. f(x)=1,5*x^4-2*x³+1,4*x²+0,1*x => f'(x)=6*x³-6*x²+2,8*x+0,1 => f"(x)=18*x²-12*x+2,8 f"(x) = 18 * [(x - 1/3)² + 0,4/9] ---> strictement positive car ... Si on préfère, on calcule le discriminant de f''(x) : Delta = 12² - 4*18*2,8 = -57,6 < 0 Et donc f"(x) a, pout tout x, le signe de son coefficient en x², soit positif f"(x) > 0 --> f'(x) est strictement croissante f'(0) = 0,1 > 0 Des 2 lignes précédentes on conclut que f'(x) > 0 et que donc f est strictement croissante. f(0) = 0 f(1) = 1 Il y a alors tout ce qu'il faut pour faire le tableau de variations de f sur [0 ; 1]

Bonjour, Ex1. 1a) Cas A : prix = 4 * 5 = 20 euros Cas B : prix = 15 + 4 * 3 = 27 euros Cas C : prix = 40 euros 1b) Le tarif avantageux est donc le ... ******** 2) a) f(x) = 5x ... pour autant que les x entrées soient faites endéans 1 mois b) linéaire ******** 3) a) g(x) = 15 + 3x b) f est croissante sur [1 ; 10] car ... ******** 4) h(x) = 40 ... pour autant que les x entrées soient faites endéans 1 mois ******** 5) Fais le graphique pour x dans [1 ; 10] de f(x) = 5x, de g(x) = 15 + 3x et de h(x) = 40 en respectant les contraintes (1 cm pour 1 entrée sur l’axe des abscisses et 1 cm pour 5 euros sur l’axe des ordonnées) A comprendre et ensuite faire les points 6 à 8... ******************* Ex 2 A1) A(5;8) et B(13;21) f(x) = ax + b On arrive au système : 8 = 5a + b 21 = 13a + b qui résolu (fais-le) donne a = 0,625 et b = -0,125 f(x) = 1,625.x - 0,125 A2) Il faut vérifier si les coordonnes du point C vérifie y = 1,625.x - 0,125 ... fais-le et conclus. B) Plusieurs méthodes possibles. Placer (avec précision) les points dans un repère orthonormé et vérifier visuellement si les 3 points sont alignés ... Calculer le coefficient directeur de (AB) : m1 = (-1 - 0)/(0 - (-2)) = -1/2 Calculer le coefficient directeur de (AC) : m2 = ... Et conclure en comparant les valeurs de m1 et m2

Bonjour, Voir le dessin. Le triangle a une base de valeur 1 (en rouge) Le triangle a une hauteur de valeur 1 (en bleu) Son aire = (1/2) * base * hauteur = 1/2 * 1 * 1 = 1/2 = 0,5 ******* Avec le point de la courbe de coordonnées (0,8 ; 0,57) ... Cela signifie que les 80 % les moins riches de la population disposent de 57 % de la totalité des revenus. Donc le reste de la population (qui est forcément les 20 % les plus riches) disposent de 100 % - 57% = 43 % des revenus. N'est-ce pas évident ? ********

Bonjour, 2) Sur le graphique, on détermine le point d'abscisse 0,8 .... on trouve (0,8 ; 0,57) (à la précision de lecture près) Donc 80 % de la population la moins riche dispose de 57 % des revenus. Et Donc, les 20 % de la population la plus aisée disposent de (100 - 57) = 43 % des revenus ******* 3a) On peut calculer l'aire comprise entre la courbe et l'axe des abscisses (pour x allant de 0 à 1) par Intégrale(de0à1) f(x) dx Intégrale(de0à1) f(x) dx = Intégrale(de0à1) (1,5x^4-2x^3+1,4x^2+0,1x) dx ... fais le. On arrive à Intégrale(de0à1) f(x) dx = 0,317 (arrondi) L'aire du triangle est (1 * 1)/2 = 0,5 Et donc l'aire hachurée = 0,5 - 0,317 = 0,183 L'indice de Gini est C = 0,183/0,5 = 0,366 (à arrondir à 0,37)

Bonjour, Ecris ce que tu as déjà fait ... On pourra alors t'aider à corriger tes erreurs ... si il y en a. ***** Si ton schéma utilise les notations usuelles, la tension d'entrée (notée E) vaut 0 Volt et puis passe instantanément à une tension de E volts continu. - Que vaut alors le courant dans le circuit tant que la tension d'entrée est 0 ... et que vaut la tension Vs ? - A l'instant où la tension d'entrée passe de 0 à E volts, que vaut le courant dans le circuit ... et pourquoi ? (penser à l'inductance L) Tu pourras alors en déduire la valeur de Vs à cet instant. - Comment évolue le courant dans le circuit après le passage de la tension d'entrée de 0 à E volt ... et quelle est la valeur vers laquelle tend ce courant en temps très long ? Est-ce une valeur constante ou non ? En répondant à cette question, tu pourras déduire la valeur vers laquelle tend Vs en temps très long. ****** Si E n'est pas une tension échelon, mais une tension sinusoïdale ... il faut le savoir. Mais dans ce cas, la notation "E" n'est pas vraiment adéquate.

Bonjour Il manque un mot dans l'énoncé. La combustion d'un gramme de carbone nécessite 10L ...

Bonjour, Oui, avec x dans C : Exemple : e^x + a = 0 avec a > 0 Solutions : x = ln(a) + i.Pi*(1 + 2k) avec k dans Z **** Que l'on vérifie : e^x = e^(ln(a) + i.Pi*(1 + 2k)) = e^ln(a) * e^(i.Pi*(1 + 2k)) = a * (cos((1+2k)Pi) + i.sin(1+2k).Pi)) = a * (-1 + 0*i) = -a

Etude simplifiée. Moment des forces autour de C : P * L/2 - F * BC.sin(alpha) = 0 avec P = 15 * (9 + 3) = 180 kN L = 9 + 3 = 12 m F la force exercée par le poteau sur la dalle. 180.10^3 * 12/2 - F * 9 * sin(66°) = 0 F = 131357 N Il a aussi la réaction en C comme force sur la dalle. Soit Rcv la composante verticale (vers le haut) de cette force et Rch la composante horizontale (vers la gauche) de cette force. On a : F * sin(alpha) - P + Rcv = 0 F * cos(alpha) - Rcv = 0 131357 * sin(66°) - 180000 + Rcv = 0 131357 * cos(66°) - Rch = 0 Rcv = 60000 N Rch = 53428 N |Rc| = 80340 N ****** Erreurs de calculs incluses ... rien relu. Pour l'étude affinée, le principe est le même. Mais, il faut tenir compte que les 180 kN qui est l'équivalent de la charge répartie pour l'étude simplifiée, doivent ici être remplacés par 3 forces, 2 de ces forces étant dues à la répartition différente de la neige et la 3ème par le poids des rochers. ...

Bonjour, C'est Ok ... juste des distractions dans la dernière ligne de calcul. 2e2x - ex - 1 = e2x - ex + e2x - 1 = ex(ex - 1) + (ex - 1)(ex +1) = (ex - 1)(2ex + 1)

Bonjour, Ex 1 Pour comprendre les questions, il suffit de savoir lire. Savoir ensuite y répondre demande évidemment de bien connaître son cours. Je fais le premier, sans trop détailler. MA et MB sont des rayons du cercle cherché ... et donc MA = MB MA² = (xM - 7)² + (yM - 9)² MB² = (xM + 1)² + (yM - 5)² MA = MB --> MA² = MB² et donc : (xM - 7)² + (yM - 9)² = (xM + 1)² + (yM - 5)² xM² + 49 - 14xM + yM² + 81 - 18yM = xM² + 2xM + 1 + yM² + 25 - 10yM 49 - 14xM + 81 - 18yM = 2xM + 1 + 25 - 10yM 104 - 16xM - 8yM = 0 16xM - 8yM = 104 Comme M appartient à la droite d'équation 3x + 4y = 22, les coordonnées de M satisfont cette équation et on a donc : 3xM + 4yM = 22 On a donc le système : 16xM - 8yM = 104 3xM + 4yM = 22 ... qu'il suffit de résoudre. 16xM - 8yM = 104 6xM + 8yM = 44 On ajoute ces équations membre à membre et --> 22 xM = 148 xM = 148/22 = 74/11 et 4yM = 22 - 3*74/11 = 20/11 yM = 5/11 On a donc M(74/11 ; 5/11) On peut calculer le rayon du cercle en calculant la valeur de MA = RacineCarrée((xM - 7)² + (yM - 9)²) en remplaçant xM et yM par les valeurs trouvées. ********** Voila, il te faut comprendre tout cela et le présenter correctement. Recopier sans comprendre est inutile. ********** Essaie le 2 et écris ce que tu as fait, même si ce n'est pas complet. Il faut évidemment commencer par étudier son cours. Il y aura bien un ou l'autre pour t'indiquer tes erreurs.

Bonjour, Juste pour embêter un peu le bazar, Dans tous les cas dessinés, les surfaces balayées par les cordes débordent de la cour et donc si celle-ci est clôturée ou fermée matériellement d'une manière quelconque (comme c'est quasi toujours le cas), il est impossible de faire tourner les cordes à partir des points indiqués. Mais pourquoi s'embêter avec de tels détails ? ... Si ce n'était de développer l'esprit critique des élèves.

Bonjour, Mesurer sur le dessin est probablement ce qui est attendu puisqu'on ne peut pas utiliser la trigonométrie... Mais alors, il est impératif de dessiner correctement à l'échelle ... par exemple ne pas avoir un angle de 38° qui sur le dessin en fait 45° ou encore avoir une distance de 1 m dessiné qui est loin à l'échelle d'être 26 fois plus petite que la longueur de 26 m dessinée.

Bonjour, Attention ... Ecrire c1=(5000+10%)-570 est mathématiquement litigieux Ce serait plus judicieux d'écrire : c1 = 5000 * (1 + 10/100) - 570 c1 = 5000 * 1,1 - 570 c1 = 5500 - 570 c1 = 4930 ***** Même remarque sur l'écriture c(n+1)=c(n)+10%-570 ... c(n+1) = 1,1 * c(n) - 570 ***** 3) z = 1,1z - 570 U(n) = c(n) - z U(n+1) = c(n+1) - z U(n+1) = 1,1 * c(n) - 570 - z U(n+1) = 1,1 * c(n) - 570 - (1,1z - 570) U(n+1) = 1,1 * c(n) - 1,1z U(n+1) = 1,1.(c(n) - z) U(n+1) = 1,1 * U(n) Donc Un est géométrique de raison 1,1 U0 = c0 - z avec z = 5700 U0 = c0 - 5700 U0 = 5000 - 5700 U0 = -700 U(n) = U0 * 1,1^n U(n) = -700 * 1,1^n c(n) = u(n) + z c(n) = 5700 -700 * 1,1^n ******

Bonjour, 1, 2 et 3 : On te demande d'utiliser ta calculette pour y entrer la fonction f(x) = x³-45x²+663x-2700 et calculer les valeurs de f(x) pour les différentes valeurs de x données dans le tableau La marche à suivre dépend de la calculette que tu utilises et c'est à toi de savoir (ou d'apprendre) comment y faut procéder avec cette calculette. Quand ce sera fait, avec les résultats fournis par la calculette tu pourras remplir le tableau. Les valeurs à trouver sont ci-dessous (mais tu dois arriver à les retrouver toi-même en utilisant correctement ta calculette) x f(x) 10 430 11 479 11,5 494,125 11,75 499,671875 12 504 12,25 507,203125 13 511 14 506 14,25 503,578125 14,5 500,875 14,75 497,984375 17 479 18,25 490,328125 18,5 495,875 18,75 502,734375 20 560 --------- 4) En regardant le tableau obtenu, comme f est une fonction continue sur R, on peut dire que pour x compris dans [10 : 20], f(x) = 500 pour une valeur de x comprise dans ]11,75 ; 12[ et aussi pour une autre valeur ce x comprise dans ]14,5 ; 14,75[ et aussi pour une autre valeur ce x comprise dans ]18,5 ; 18,75[

Bonjour, 1) Attention, tu as noté 25/225 au lieu de 27/225 dans tes réponses. ex 2: 3) Avec les jatrophas 5/3 est faux. Ta réponse signifierait qu'il y a plus de jatrophas qu'il n'y a d'arbres (dont les jatrophas) au total. Et donc ... 4) Attention ... les arbres plantés par Virgilio dans la question 4 viennent s'ajouter à ceux déjà plantés par Virgilio dans la question 3 et attention aussi de ne pas refaire le même genre d'erreur que dans la question 3.

Bonjour, J'en fais un en exemple ... à toi pour les autres. Je fais le n° 2 - On trace le cercle trigonométrique (de centre O et de rayon 1) J'ai repéré sur le dessin, l'axe des sinus et l'axe des cosinus ainsi que les angles 0, Pi/2 , Pi , 3Pi/2 et 2Pi (qui est sur le dessin confondu avec l'angle 0) On repère l'intervalle d'angle donné par l'énoncé qui ici est [Pi/2 ; Pi] ... je l'ai marqué en vert sur le dessin. (c'est le 2ème quadrant) On sait que sin(x) = 3/5, on marque donc 3/5 sur l'axe des sinus ... L'angle x compris dans [Pi/2 ; Pi] qui correspond à sin(x) = 3/5 correspond au point M comme montré sur le dessin. On trouve son cosinus en suivant les flèches en gris sur le dessin ... et on lit donc que ce cosinus est négatif. Sachant que cos(x) < 0 et que sin(x) = 3/5 et que cos²(s) + sin²(x) = 1, on calcule [tex]cos(x) = - \sqrt{1 - (\frac{3}{5})^2} = - \frac{4}{5}[/tex] ************* Voila, à toi pour les autres. Zut, j'oublie chaque fois, que Latex ne fonctionne pas sur ce site. A la fin de mon message précédent, lire : ... Sachant que cos(x) < 0 et que sin(x) = 3/5 et que cos²(s) + sin²(x) = 1, on calcule cos(x) = - RacineCarrée[1 - (3/5)²)] = -4/5

"Je sais bien qu'on aurait pu faire une recherche sur la toile," Peut-être ou peut-être pas. J'ai imaginé cette méthode, sans l'avoir vue nulle part, à partir de la valeur exacte du cosinus. Il est probable que d'autres l'avaient fait avant ... mais je n'en sais rien. N'importe quoi.

Bonjour, Voila, c'est évidemment mieux dessiné que sur mon dessin fait en mesurant sur l'écran de mon ordi sans logiciel particulier.

Bien sûr que si, mais tu n'as pas compris ma construction. D n'est pas sur le cercle, même si il en est très proche. ********* Quand on a construit AC (qui vaut (1 + V5).R) On divise cette longueur par 4 au compas et on obtient la longueur AD (qui vaut R * (1 + V5)/4) (D n'est pas sur le cercle mais en est très proche) On mesure au compas la longueur AD et on la reporte sur l'axe horizontal à partir de O ... on a donc AD = OE = R * (1 + V5)/4 En "relevant" le point E sur le cercle, on obtient le point F et l'angle AOF vaut Pi/5 car son cosinus vaut OE/R soit (1 + V5)/4 er comme cos(Pi/5) = (1 + V5)/4 ...

Oui et alors ? Je ne force personne à regarder mes réponses.

Bonjour, Juste pour le fun, construction a la latte non graduée et au compas d'un angle Pi/5 Et quand c'est fait, on peut évidemment avoir tous les "multiples" de Pi/5.