Black Jack

Cela, çà ne veut rien dire. julesx t'a donné ce qu'on pouvait déduire, soit : "Au point d'abscisse 0, Cf coupe la droite"

Bonjour, 3) h(x) = x (1 - e^(x²-1)) (1 - e^(x²-1)) 0 sur [-1 ; 1] (avec (1 - e^(x²-1)) = 0 en x = -1 et x = 1) Donc sur ]-1 ; 1[, h(x) a le signe de x. Donc : h(x) = 0 pour x = -1 h(x) < 0 pour x dans ]-1 ; 0[ h(x) = 0 pour x = 0 h(x) > 0 pour x dans ]0 ; 1[ h(x) = 0 pour x = 1 Donc : Cf coïncide avec d pour x = -1 Cf est au dessus de d pour x dans ]-1 ; 0[ Cf coïncide avec d pour x = 0 Cf est en dessous de d pour x dans ]0 ; 1[ Cf coïncide avec d pour x = 1 La courbe Cf en x = 0 coïncide avec l'origine du repère.

@volcano47, Bonjour, J'ai un peu de mal à te comprendre. Ex 2) A) On lit sur le graphique : f(2) = 4 et f'(2) = 2 Il n'y a aucune ruse fa la part du prof. La tangente "semble" être la bissectrice ... n'implique en rien que f'(2) = 1 Ici, les graduations de l'axe des abscisses sont différentes de celui de l'axe des ordonnées et c'est ce qui cause ici ta mauvaise interprétation. On a donc f'(2) = 2 = (-2a*2² + (6a-b)*2 + 2b)/RacineCarrée(2*(4-2)) (-8a + 12a - 2b + 2b)/RacineCarrée(4) = 2 4a*2 = 2 a = 1 et avec f(2) = 4 --> (1*2 + b)*racine(2*(4-2)) = 4 (2 + b) * 2 = 4 b = 0 OK ?

Oui, on n'a pas tous la même approche. S'imaginer qu'une méthode pas à pas fonctionne est une illusion. Indiquer le chemin à suivre à chaque carrefour, comme un GPS n'a jamais fourni à personne le sens de l'orientation. Et, dans une grande majorité des cas, l'aide partielle reçue est utilisée par l'aidé pour faire croire sur un autre site qu'il a cherché et un peu avancé ... pour y solliciter une autre partie de l'aide et d'aller retour en aller retour sur quelques sites, tout est quand même fait par les aidants. Et pire que tout, après cette aide GPS, l'aidé pense qu'il a fini par y arriver, énorme illusion.

Bonjour, Certaines parties de l'énoncé me semble tirés par les cheveux. Si p/q (avec p et q premiers entre eux) est solution de x³ - x² - 2x + 1 = 0 alors on a : (p/q)³ - (p/q)² - 2p/q + 1 = 0 p³ - p²q - 2pq² + q³ = 0 p³ - p²q + q³ = 2pq² La suite est pour moi idiote telle que présentée... je fais alors autrement. ''''''' a) Si p et q sont impairs, alors (p³ - p²q + q³) est impair car ... et 2pq² est pair Donc l'équation p³ - p²q + q³ = 2pq² n'a pas de solutions b) Si p est pair et q impairs, alors (p³ - p²q + q³) est impair car ... et 2pq² est pair Donc l'équation p³ - p²q + q³ = 2pq² n'a pas de solutions c) Si q est pair et p impairs, alors (p³ - p²q + q³) est impair car ... et 2pq² est pair Donc l'équation p³ - p²q + q³ = 2pq² n'a pas de solutions d) p et q pairs est interdit puisque p et q sont premier entre eux. Donc, quels que soient p et q (premiers entre eux), l'équation p³ - p²q + q³ = 2pq² n'a pas de solutions En supposant que p/q (avec p et q premiers entre eux) est solution de x³ - x² - 2x + 1 = 0, on montre que c'est impossible (par les 4 cas ci-dessus) Et donc l'équation x³ - x² - 2x + 1 = 0 n'a pas de solutions rationnelles. (1) *** L'équation n'a pas non plus de solution entière car cela impliquerait que x³ - x² + 1 = 2x avec x entier. En effet si x est impair, x³ - x² + 1 est impair et x est pair ... donc pas possible. et si x est pair, x³ - x² + 1 est impair et x est pair ... donc pas possible. Donc l'équation x³ - x² + 1 - 2x = 0 n'a pas de solutions entières. (2) *** (1) et (2) --> l'équation x³ - x² + 1 - 2x = 0 n'a pas de solutions entières et n'a pas de solutions rationnelles. '''''''''''''''' Pour moi, l'énoncé est sujet à caution, en effet, en 2a, on écrit : Expliquer pourquoi 2pq² = 0 ... alors qu'il a été supposé que p et q étaient premiers entre eux, donc ni p ni q ne peut être nul. '''''''''''''''' Peut-être qu'un autre aidant aura une idée pour aller dans le sans des questions telles qu'elles sont posées ... dont certaines sont, pour moi, bancales.3 ''''''''''''''''' Je change d'avis sur la présentation de l'énoncé, je n'avais pas vu les modulo 2 dans la question 2. Tu peux donc le faire en suivant l'énoncé, ce que j'ai fait peut t'y aider.

Bonjour, Nombre de cellules : 30000.10^9 = 3.10^4 * 10^9 = 3.10^13 ***** Nombre de bactéries : 10^14 + 10^12 + 3.10^11 + 2.10^7 = 10^13*(10^1 + 10^-1 + 3.10^-2 + 2.10^-6) = 10,130002.10^13 ********** rapport (Nbre bactéries)/(Nbre cellules) = 10,130002.10^13/(3.10^13) (Nbre bactéries)/(Nbre cellules) = 10,130002/3 = 3,38 arrondi ********** Ou bien : (Nbre bactéries)/(Nbre cellules) = (10^14 + 10^12 + 3.10^11 + 2.10^7)/( 3.10^4 * 10^9) (Nbre bactéries)/(Nbre cellules) = (10^14 + 10^12 + 3.10^11 + 2.10^7)/( 3.10^13) (Nbre bactéries)/(Nbre cellules) = (10^1 + 10^-1 + 3.10^-2 + 2.10^-6)/3 (Nbre bactéries)/(Nbre cellules) = 10,130002/3 = 3,38 (arrondi) Mais, tu dois essayer par toi-même, envoyer ce que tu trouves sur le site (et pas se contenter, d'un "Je n'y arrive pas")... Il y aura alors bien un ou l'autre aidant qui pourra te corriger si nécessaire.

Bonjour, Si tu ne tentes pas par toi-même, tu n'apprendras rien. Essaie de comprendre ce qui suit et repose des questions sur ce que tu ne comprends pas... *** Ce sont des applications assez simples de la loi des mailles et de la loi des noeuds. Il faut aussi connaître des caractéristiques simples des transistors. Gain DC du transistor = IC/IB = 120 (voir sur schéma) V(AC) = Rc * IC= 200.Ic V(CE) = Vcc/2 = 12/2 = 6 V V(EM) = RE * IE Or IE = IC + IB = 120 IB + IB = 121 IB = 121/120 IC (souvent on utilise IE = IC comme toute bonne approximation) V(EM) = RE * (121/120) * IC Vcc = V(AC) + V(CE) + V(EM) 12 = 200.IC + 6 + RE * (121/120) * IC (200 + RE * (121/120))*IC = 6 Or IB = 0,1 mA --> IC = 120 * 0,1 = 12 mA (12.10^-3 A) (200 + RE * (121/120)) * 12.10^-3 = 6 (200 + RE * (121/120)) = 500 RE * (121/120) = 300 RE = 300 * 120/121 = 298 ohms (et on trouverait RE = 300 ohms si on faisait l'approximation IE = Ic) ********** V(EM) = RE * IE presque = RE * Ic = 300 * 12.10^-3 = 3,6 V V(BM) = V(EM) + V(VE) = 3,6 + 0,6 = 4,2 V I(BZ) = 5 * IB = 5 * 10^-4 = 5.10^-4 A V(BM) = RB2 * I(BZ) 4,2 = RB2 * 5.10^-4 RB2 = 8400 ohms ********* V(AB) = Vcc - V(BM) = 12 - 4,2 = 7,8 V IB1 = IB + I(BZ) (loi des noeuds) IB1 = 5.10^-4 + 10^-4 = 6.10^-4 A RB1 = V(AB)/IB1 RB1 = 7,8/(6.10^-4) RB1 = 13000 ohms ********* Recopier sans comprendre ne sert à rien.

Bonjour, Tu devrais au minimum essayer par toi-même. On ne sera pas là pour répondre à ta place pendant une interrogation en classe ... ou aux examens. Voila une aide, plus que substantielle, qui ne servira pas pour le futur sans effort de ta part. 2) Soit x la quantité de macarons disponibles avant la 1ère vente. Le 28 juin ... a vendu les 3/5 de sa marchandise... Mr Carvin a donc vendu (3/5).x macarons Après cette vente, il reste donc en magasin x - (3/5).x = (2/5).x macarons Le 29 Juin .. Mr Hannebicq achète 2/4 de ce qui restait en magasin, elle achète donc (2/4) * (2/5).x = (1/5).x macarons Après cette opération, il reste donc en magasin : (2/5).x - (1/5).x = (1/5).x macarons en magasin. La quantité de macarons vendue depuis le début est donc : (3/5).x + (1/5).x = (4/5).x L'énoncé précise que les x macarons de départ avaient une valeur de 1400 euros. x macarons coûtent 1400 euros. (x/5) macarons coutent 1400/5 = 280 euros. ************* A toi de comprendre tout cela (et pouvoir le refaire seul). Si tu y arrives, alors tu pourras rédiger sans soucis les réponses aux 4 questions posées.

Bonjour, ex1 1) I = 200 µA, donc > 0 et alors la flèche sur le schéma correspond au sens conventionnel du courant. A savoir : les électrons ont un sens de circulation opposés au sens conventionnel du courant. ... et donc, ici, les électrons ont un sens de droite à gauche sur le dessin. 2) Q = I*t avec Q (en C) la variation de charge due au passage du courant I (en A) pendant une durée t (en s) Q = 200.10^-6 * 10.10^-3 = 2.10^-6 C Et la charge Q correspond à la charge d'un nombre N d'électrons de charge élémentaire q = 1,6.10^-6 C --> Q = N*q 2.10^-6 = N * 1,6.10^-19 N = 1,25.10^13 (a arrondir à 2 chiffres significatifs ?) Remarque : la charge d'un électron est négative (même si ce n'est pas indiqué ainsi dans l'énoncé) ********************** Exercice 3 Dessins de gauche : indication : 5 A Indication : 20 mA Indication : - 60 µA dessin de droite : I1 = -5 A I2 = 5 A I3 = I1 - I2 = -10 A I2 "entre" dans l'ampèremètre par sa borne - et donc il indique une valeur de signe contraire au courant conventionnel ... L'indication de l'ampèremètre est donc 10A ********************** La prochaine fois, demande des explications via le site. Il faut évidemment comprendre les réponses, sinon cela ne sert à rien.

Bonjour, Exercice 2 Simples applications de la loi des noeuds. Ex 2 : Avec les courants en mA I1 = I2 + I3 5 = I2 + 3 I2 = 2 mA I3 + I6 + I4 = 0 3 + 1 + I4 = 0 I4 = -4 mA I7 = I1 I7 = 5 mA I5 = I6+I7 I5 = 1 + 5 I5 = 6 mA

Bonjour, Une approche "énergétique". En t = 0, le palet a une énergie cinétique Ec = 1/2.m.Vo² Hors pertes par frottement, cette énergie cinétique va se "transformer" en énergie potentielle (m.g.delta h) et le mobile aura son altitude augmentée de delta h 1/2.m.Vo² = m.g.delta h delta h = Vo²/(2g) Avec alpha l''angle du plan incliné par rapport au plan horizontal, on a : delta h = OB * sin(alpha) Donc : OB = Vo²/(2g.sin(alpha)) **** Hors frottement, il y a conservation de l'énergie mécanique et donc lorsque le palet repassera en O, la vitesse sera vo ... mais dans le sens de la descente. ******************** Autre approche : Avec t = 0, l'instant du lancer : Avec le repère du dessin : L'accélération du palet est a = g.sin(alpha) (sens vers le bas du plan incliné) on a donc v(t) = -Vo + g.t.sin(alpha) dx/dt = -Vo + g.t.sin(alpha) x(t) = -Vo.t + gt²/2 * sin(alpha) Le mobile arrive en B pour la valeur de t qui annule v(t) --> pour t = Vo/(g.sin(alpha)) xB = -Vo.Vo/(g.sin(alpha)) + g(Vo/(g.sin(alpha)))²/2 * sin(alpha) xB = -Vo²/(g.sin(alpha)) + (Vo²/(2g.sin(alpha)) xB = Vo²/(2g.sin(alpha)) --> |OB| = Vo²/(2g.sin(alpha)) **** Lorsque le mobile repasse en O, x(t) = 0 (avec t > 0) --> -Vo.t + gt²/2 * sin(alpha) = 0 gt²/2 * sin(alpha) = Vo.t gt/2 * sin(alpha) = Vo t = 2Vo/(g.sin(alpha)) La vitesse est, à cet instant : v = -Vo + g.t.sin(alpha) = -Vo + g*2Vo/(g.sin(alpha))*.sin(alpha) v = -Vo + 2Vo v = Vo Vitesse de même norme et même direction qu'au lancer, mais de sens contraire. ********** A comprendre évidemment et pouvoir refaire seul(e) ensuite.

Bonjour, Tu devrais écrire sur le site ce que tu as trouvé. Sauf erreur ou distraction de ma part, le champ électrique résultant au centre du carré est de 15910 V/m (donc environ 1,6 cm à l'échelle demandée) et il est dirigé vers la gauche suivant l'axe des abscisses du dessin. Calculs non vérifiés.

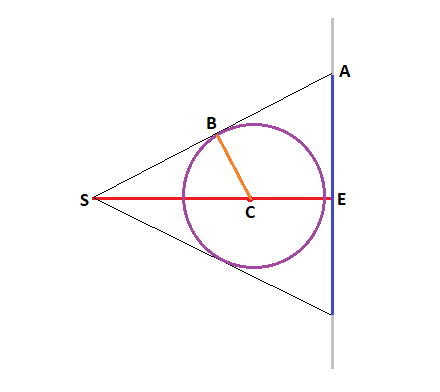
Bonjour, Enoncé ambigu Que signifie : "distance de la source à la sphère de 0,40 m" Est-ce la distance entre la source et le centre de la sphère ou bien la distance entre la source et le point de la sphère qui lui est le plus proche ? Avec les valeurs numériques données des distances, je présume que la distance de la source à la sphère dont on parle est celle entre la source et le centre de la sphère ... mais cela DEVRAIT être explicitement écrit dans l'énoncé. Et donc, sous réserve que 0,40m soit bien la distance entre la source et le centre de la sphère , on a : SE = 0,6 (m) SC = 0,4 (m) AE = 0,30 m Pythagore dans le triangle SEA --> SA² = AE² + SE² = 0,45 SA = RacineCarrée(45) Les triangles SAE et SCB sont semblables (de même forme dit-on aujourd'hui) car ils ont leurs angles égaux 2 à 2 ... Donc on a : SA/SC = AE/CB BC = AE * SA/SC BC est le rayon de la sphère calculable puisque on connait les longueurs AE, SA et SC.

Bonjour, Je ne suis pas prof et encore moins correcteur du bac ... et donc mon avis vaut ce qu'il vaut. D'abord, félicitation pour l'ensemble de ton travail qui est "presque" parfait. En survolant tes réponses, je note quelques "imperfections", les réponses finales sont correctes, mais il y a quelques "indélicatesses" dans la rédaction, et c'est peut être celles-ci qui ont été sanctionnées par le correcteur. Exemples : - Dans l'exercice 2, tu emploies le mot "déterminant" au lieu de "discriminant". - Plusieurs fois, dans un travail sur les limites, tu "oublies" de noter vers quoi tend la variable (exemple (entre d'autres) tu écris lim 9-6e^(-0,19(n-1)) = 9 en "oubliant" le pour n --> +oo)) Et quelques autres indélicatesses du même type. Si le correcteur les voit, je présume qu'elles sont repérées par son "crayon rouge" et qu'ils en tient compte dans la cote finale en retirant quelques points.

Bonjour, Une réflexion... Si le site (avec le lien) indique que on ne peut pas mettre des transfos Yy6 et Dd10 en parallèle ... Soit le site se trompe, soit il y a une vraie raison. Que cela ait été ou non vu au cours, les 4 conditions données dans ma réponse précédente doivent être respectées. Supposons que les transfos, coté basse tension distribuent du triphasé 3 X 400 V plus neutre (pour les utilisations en mono 230 V). La tension entre le neutre et chacune des phases est 230 V ... mais les charges sur ces tensions 230 V, si elles sont déséquilibrées (comme c'est toujours le cas) génèrent du courant dans le fil de neutre. Or le fil de neutre est "accroché" au seul générateur Yy et donc le courant de neutre passe uniquement dans les enroulements du transfo Yy et pas dans le Dd. Ceci provoque alors des chutes dans les enroulements du Yy qui ne se retrouvent pas dans le transfo Dd, il y a déséquilibre entre les chutes de tension dans les 2 transfos et la 4 ème condition n'est pas respectée.

Bonjour, Avec bien du retard ... On mesure sur le dessin supposé à l'échelle et on trouve que la largeur de la tour est de 19 m (en bleu) Donc BD = BC + 19/2 = 69,5 m BS = BD/cos(67°) BS = 69,5/cos(67°) = 177,9 m ... et donc à l'échelle denadée : 17,79 cm Et pas demandé : hauteur = BS * sin(67°) = 163,8 m Ce qui est loin de la réalité (142 m) ***** Donc, je présume que l'auteur de l'énoncé s'est mis le doigt dans l'oeil et n'a pas remarqué que le triangle BCS n'était pas rectangle ... ce qui rejoint la remarque de julesx.

Oui Jules, Autant que maintenant je m'en souvienne. Il faut 4 conditions pour pouvoir mettre des transfos en parallèle. a) Même rapport de transformation b) même ordre de succession des phases c) même groupe d'indice horaire Ces 3 premières conditions satisfont la mise en parallèle de transformateurs A VIDE Il y a une 4ème condition pour pouvoir charger ces transformateurs ... d) Il faut qu'ils aient des mêmes chutes de tension sous toutes les conditions de charges. (même à la mise en court-circuit) ********* C'est probablement à cause de cette 4ème condition que la mise en parallèle d'un Yy6 avec un Dd10 est interdite. Mais cela mériterait une plus ample investigation.

Bonjour, Je tente d'expliquer, pour autant que je m'en souvienne (et donc méfiance) ... Le groupe I est pour les indices horaires 0 , 4 et 8 Le groupe II est pour les indices horaires 6, 10 et 2 Le groupe III est pour les indices horaires 1 et 5 Le groupe IV est pour les indices horaires 7 et 11 Les indices horaires donnent les déphasages par multiple de 30° entre les tensions des enroulements primaires et secondaires. Donc par exemple un Yy6 a un déphasage de 6*30 = 180° entre les tensions des enroulements primaires et secondaires. Il est possible de mettre en parallèle des transformateurs dont les indices horaires sont différents d'un multiple de 4 (donc avec des déphasages primaires secondaires différents d'un multiple de 120°) Pour que cela fonctionne, il faut , bien entendu connecter les enroulements pour que les tensions secondaires des transformateur se retrouvent en phase sur chacun des enroulements (et ceci grâce au déphasage de 120° ou 240° qui existe naturellement entre des tensions d'alimentations triphasées) Si on a par exemple des transfos Yy6 et Yy10, comme 10-6 = 4 (multiple de 4, il est possible de les mettre en parallèle) Pareillement, on pourrait mettre en parallèle des transfos Dd8 et Dd0 (puisque 8-0 = 8 qui est multiple de 4) Cela c'est assez facile, il suffit de regarder si les transfos sont du même groupe. MAIS ... Cela est vrai avec soit des transfos tous Yd ou tous Dd Mais si on mélange des sortes de transfos, il faut tenir compte qu'il y a un déphasage de 30° entre les tensions des bobinages en triangle (D) ou en étoile (Y) Et donc par exemple si on a un transfo Yy6 et un transfo Dd10 ... ils semblent être tous les deux dans le groupe II. Et pourtant on ne peut pas les mettre en parallèle car, les bobinages primaires des 2 transfos reçoivent des tensions déphasées de 30 °C ... et donc les secondaires seront aussi déphasées de 30° et donc pas possible de les avoir en phase. Voila, aux conneries de ma part près.

Je n'ai jamais écris que les 12 kg d'eau atteignait la température de 0°C Ce calcul, qui aboutit ici à Q4 > Q3 permet uniquement de démontrer que l'état final sera entièrement liquide à une température positive. Ce qui permet alors une suite de résolution très facile. Si on n'avait pas trouvé Q4 > Q3, alors il fallait investiguer plus loin pour voir si ce n'était pas l'eau liquide initiale qui passait à l'état de glace et température finale négative ou bien si on aboutissait à un "mélange" eau-glace à 0°C. Cette manière de faire est parfaitement licite et permet facilement de déterminer l'état final (tout liquide ou tout glace ou un "mélange eau-glace" alors à 0°C) et donc on sait où on va et les calculs à mener sont faciles. Ce n'est évidemment pas la seule manière de faire ... mais cette méthode n'a rien de critiquable.

Bonjour, Voir ici par exemple : http://lycees.ac-rouen.fr/maupassant/Melec/co/Reseau_HTABT/Couplage_transfo_tri/web/co/module_Couplage_transformateur_3.html Les réponses sont : Groupe II Non Non

Bonjour, Quantité de chaleur nécessaire pour amener 3 kg de glace de -18°C à 0°C (sans changement d'état) : Q1 = 3 * 0,5 * 18 = 27 kcal Quantité de chaleur nécessaire pour faire passer 3 kg de glace de l'état solide à l'état liquide à 0°C : Q2 = 3 * 80 = 240 kcal Et donc : Quantité de chaleur nécessaire pour amener 3 kg de glace de -18°C à l'état liquide à 0°C : Q3 = Q1 + Q2 = 267 kcal **** Quantité de chaleur cédée pour amener 12 kg d'eau de 50P°C à 0°C (sans changement d'état) : Q4 = 12 * 1 * 50 = 600 kcal **** Q4 > Q3 ... et donc l'état final sera une masse d'eau liquide de 30+3 = 33 kg à une température positive Tf **** On a donc (avec les quantités de chaleur en kcal) : 267 + 3 * 1 * (Tf - 0) + 12 * 1 * (Tf - 50) = 0 267 + 3.Tf - 600 + 12.Tf = 0 Tf = 333/15 = 22,2 °C Sauf distraction ... A comprendre et corriger au besoin.

1) 2Al + 3S → Al2S3 2) M(AL) = 27 g/mol M(S) = 32 g/mol On utilise donc 1 mol de Al, il faut donc 3/2 mol de S, soit 48 g de S (au minimum) 3) Rien ne se perd, rien ne se crée et donc ...

Bonjour, Il me semble que l'adresse devrait être : https://www.cjoint.com/doc/23_03/MCClirsnWRm_SujetDevoirMaison1-OD-1-.pdf

Bonjour,