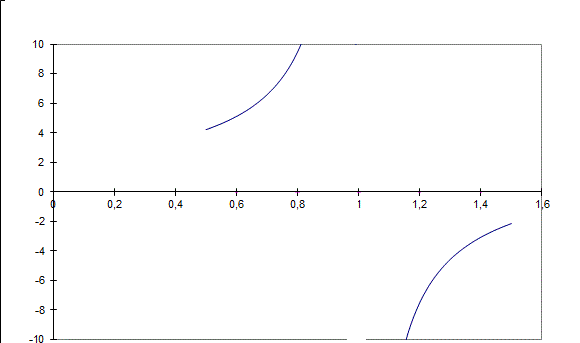Black Jack

Bonjour, Je fais le premier et donne des indications pour les suivants. 2) A = (x-2)(x+1)-(6x-5)(x-2) A = (x-2).(x+1-(6x-5)) A = (x-2).(x+1-6x+5) A = -(x-2).(5x-6) B) Mettre (4x+3) en facteur ... C) De la forme (a²-b²) = (a-b)(a+b) ... D) De la forme : (a-b)² = a² - 2ab + b² E) De la forme : (a+b)² = a² + 2ab + b² Voila, essaie ...

Bonjour, from random import* def point(): x=uniform(0,5) y=uniform(0,2) if y<=0.072*x**2+0.2: p=1 else: p=0 return p def echantillon(n): c=0 for i in range(n): c = c+point() return c somme = 0 somme = echantillon(500000) print(somme/500000) En lançant quelques fois le programme, la valeur sortie est : 0.399216 ; 0.400404 ; 0.399668 ; 0.400524 ... L'aire A vaut environ 0,4 * (5 * 2) = 4 unités d'aire. ************ Mais ce n'est utile que si tu fais l'effort de comprendre ce qui a été fait et pourquoi.

Bonjour, U1 = 10 n'est pas correct. Je n'ai pas lu le reste.

Bonjour, L'énoncé précise que l'armoire est alimentée en 3 X 400 V Et donc le neutre n'est pas distribué ... il n'y a pas de 230 V disponible dans l'armoire. --> on ne peut pas avoir un transfo qui nécessite du 230 V pour son alimentation. Le primaire du transfo DOIT donc être alimenté par du 400 V ... comme c'est dessiné sur le schéma fourni par julesx.

Bonjour, julesx a fait une remarque qu'il faut prendre en compte ... L'énoncé précise que l'alimentation est en triphasé 400 V (donc sans neutre). Le transfo doit donc être un 400 V primaire (et pas 230 V) et secondaire 24 V. De plus, dit et répété plusieurs fois, il n'y a au maximum que 2 contacteurs alimentés en même temps et il y a au max 3 voyants allumés simultanément ... Mais tu persistes dans ton calcul de "p appel" de comptabiliser 3 contacteurs et 4 voyants.

Bonjour, Une alternative pour la connexion des voyants. Comme leur tension nominale est la même que celle des contacteurs (24 V) ... Les voyants (H2, H3 et H4) peuvent être câblés en parallèle sur les bobines de relais (KM1, KM2, KM3) Cela revient fonctionnellement au même et cela diminue un rien le câblage (et permet de se passer d'un contact auxiliaire de ces relais ... qui pourrait ne pas être disponible). Pour le nombre de relais (et de voyants), pour moi, il faut (pour comptabiliser les VA) en compter 2 et pas 3 (motif déjà expliqué).

Bonjour, En lecture rapide, je ne vois rien de mal fait. Quelques remarques : - Le cahier des charges mentionne 4 voyants ... que tu n'as pas représenté sur tes schémas. - Pour la puissance de maintien, tu as indiqué : Pm = 4 X 6 = 24 VA D'où vient le 4 ?, pour moi, il n'y a que 3 contacteurs et il ne peut y en avoir que 2 enclenchés simultanément (on n'a évidemment pas le contacteur triangle et le contacteur étoile enclenché ensemble).

Bonjour, 1.1) U(n+1) = 1,5 U(n) - n + 2 Avec n = 0, il vient : U1 = 1,5*U(0) - 0 + 2 U1 = 1,5 * 6 - 0 + 2 U1 = 11

Bonjour, ex 2 Tu as fait des erreurs. 1.a) Tu as utilisé (2-Un) au dénominateur de U(n+1) au lieu de (2+Un) ... et donc tes calculs sont faux (2 ème erreur dans le calcul de U1 qui compense l'autre erreur) Tu devrais trouver : U1 = 1,4 et U2 = (4 - 1,4)/(2 + 1,4) = 2,6/3,4 = 26/34 = 13/17 (soit environ 0,764) Et donc la réponse à 1.b n'est pas celle que tu as indiquée. *********** 2.a) Comme U(n) > 0, Un + 4 n'est jamais nul et donc ... ********** 2.b) vn = (Un - 1)/(Un + 4) v(n+1) = (U(n+1) - 1)/(U(n+1) + 4) Tu remplaces là dedans U(n+1) par (4-Un)/(2 + Un). On simplifie la relation obtenue et tu devrais arriver à montrer qu'on arrive à v(n+1) = -(2/3) * (Un -1)/(U1+4) et que donc : v(n+1) = -(2/3)*V(n) Et donc ...

Bonjour, Il faut au minimum essayer par toi même ... 1) a) Un = 1200 + 100n b) Vn = 1100 * 1,08^n Tu dois d'abord comprendre ce que je viens d'écrire ... le reste est évident.

Il fallait bien entendu lire : "J'aurais laissé passer celle là sans ta remarque déplacée." 😎

J'aurais laissé passé celle là sans ta remarque déplacée.

Erreur d'inattention ... "Si R2/R1=2, I2*I1/4" devrait être "Si R2/R1=2, I2 = I1/4" 🙃

Bonjour, Aide pour question 4 : a) Mercure : E1 = - 10,38 eV ; E2 = - 5,74 eV ; E3 = - 5,52 eV ; E4 = - 4,95 eV ; E5 = - 3,71 eV ; E6 = - 2,68 eV, E7 = - 1,57 eV et E8 = - 1,56 eV Transition : E7 --> E4 : Delta E = 4,95 - 1,57 = 3,38 eV Delta E = 3,38 * 1,602.10^-19 = 5,41476.10^-19 J Delta E = h * nu (avec h la constante de Planck = 6,626.10^-34 J.s 5,41476.10^-19 = 6,626.10^-34 * nu nu = 8,172.10^14 Hz Lambda = c/nu = 299792458 / 8,172.10^14 Lambda = 367.10^-9 m Lambda = 367 nm ***** b) Lambda = 579 nm nu = c/lambda = 299792458/(579.10^-9) = 5,178.10^14 Hz Delta E = h * nu Delta E = 6,626.10^-34 * 5,178.10^14 = 3,43.10^-19 J Delta E = 3,43.10^-19/1,602.10^-19 = 2,14 eV Il faut donc trouver la transition d'états qui donne cette variation d'énergie... On voit qu'il s'agit de la transition : E7 --> E5 En effet avec E7 = - 1,57 eV et E5 = - 3,71 eV, on trouve une variation d'énergie de 3,71 - 1,57 = 2,14 eV ****** Avec cela, on peut remplir les 2 cases blanches sur la gauche du tableau. Et si on a compris, on fait des calculs similaires pour les 3 autres cas. ********************* Pour la question 5, il faut comparer le spectre des raies d'une lampe fluocompacte avec celui du mercure ... Calculs non vérifiés.

Bonjour, C'est ton tracé qui foire. Le tracé par Excel donne bien "par valeurs inférieures + infini et par valeurs supérieures - infini"

Bonjour, Peut-être considère-t'on que le fil ED fait aussi 40 m et est un 40 mm² et que le FG fait aussi 50 m et est un 50m ... Et que FE est un gros fil court et que les 2 défauts ont chacun une résistance de 2 ohms (comme l'unique défaut du début de l'exercice) ... Avec toutes ces suppositions, on peut alors calculer Z(DE) + Z(EF) + Z(FG) = 0,068 + 0 = 0,068 ohm Et avec Rd1 = Rd2 = 2 ohms, on a alors : Id = 320/(0,068 + 2 + 2 + 0,068) = 77,4 A Et Uc = 0,068 * 77,4 = 5,26 V Mais ceci est bien tiré par les cheveux tant il faut faire de suppositions (surtout sur les valeurs présumées de Rd1 et Rd2 qui n'ont aucune raison d'être égales) Or le résultat dépend fortement de la valeur de Rd1 et Rd2 Dans le pire cas, on pourrait avoir Rd1 = Rd2 = 0 ... qui donnerait Id = 320/(0,068 + 0,068) = 2353 A et Uc = 2353 * 0,068 = 160 V Va donc savoir, ce que l'auteur de la question avait dans la tête. Calculs non vérifiés.

Bonjour, Bonjour, Il manque plein d'infos dans tes énoncés, par exemple les résistances des défauts et d'autres choses. L'impédance pour le courant à 2 défauts est : Z = Z(AK) + Z(AB) + Z(BC) + Rd2 + Z(DE) + Z(EF) + Z(FG) + Rd1 + Z(HJ) + Z(JK) Il est possible (mais cela DOIT être précisé dans l'énoncé) que la chute de tension dans Z(AK) + Z(AB) + Z(JK) est prise en compte en estimant que la tension est 0,8 * V(KA). Et on a V(AK) = 400 V (attention, pas 230 V car ici on a une tension entre phase et pas entre phase et neutre) Dans ce cas; le courant de défaut est : Id = 0,8 * 400/ (Z(BC) + Rd2 + Z(DE) + Z(EF) + Z(FG) + Rd1 + Z(HJ)) En connaissant les caractéristiques du fil entre B et C (Cuivre, 40 m, 25 mm²), on trouve Z(BC) = 0,036 ohm En connaissant les caractéristiques du fil entre H et J (Cuivre, 50 m, 35 mm²), on trouve Z(HJ) = 0,032 ohm On a donc Id = 0,8 * 400/ (0,036 + Rd2 + Z(DE) + Z(EF) + Z(FG) + Rd1 + 0,032) Id = 320/ (0,068 + Rd1 + Rd2 + Z(DE) + Z(EF) + Z(FG)) Il faut donc les données pour calculer Rd1 + Rd2 + Z(DE) + Z(EF) + Z(FG). ***** Et on a Uc = U(DE) + U(EF) + U(FG) Uc = Id * (Z(DE) + Z(EF) + Z(FG)) Uc = 320 * (Z(DE) + Z(EF) + Z(FG))/ (0,068 + Rd1 + Rd2 + Z(DE) + Z(EF) + Z(FG)) ****** Pour autant que j'ai bien lu ton schéma qui n'est pas très clair et surchargé ... (Je n'ai rien vérifié).

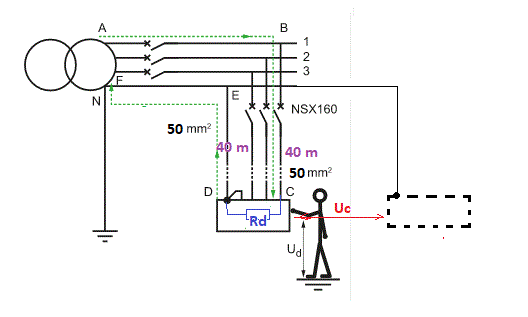
Bonjour, Schèma TT : OK ********* Schéma TN (en tenant compte de tout ce qui n'avait pas été mentionné lors de la question initiale et précisé ensuite) L'impédance du circuit pour le courant de défaut est : Z = Z(AB) + Z(BC) + Rd + Z(DE) + Z(EN) + Z(NA) Avec Z(BC), l'impédance d'un fil de 40 m en 50 mm² et avec Z(DE) l'impédance d'un fil de 40 m en 50 mm² Rd étant la résistance de défaut (supposée = 0 ohm) Z(NA) étant l'impédance du générateur de tension. ***** Z(BC) = Rho * L/S = 2,25.10^-8 * 40/(50.10^-6) = 0,018 ohm Z(DE) = Rho * L/S = 2,25.10^-8 * 40/(50.10^-6) = 0,018 ohm La chute de tension due à Z(NA) (impédance interne du générateur) + Z(AB) + Z(EN) est prise en compte par l'estimation : "... estimée à 0,8 * tension simple (Vo)) Dans le courant de défaut est Id = 0,8 * 230 /(0,018 + 0,018) = 5111 A **** Uc = U(ED) (avec Rd considérée = 0 ohm) Uc = Z(DE) * Id = 0,018 * 5111 = 92 V **** Ud n'est pas demandée dans le présent exercice. De toutes manières, avec un courant de défaut de 5111 A, le disjoncteur de protection va ouvrir le circuit très rapidement.

Bonjour, 1) On connait 2 points de la droite (AB) qui sont : A(-2 ; 3) et B(0 ; m) A partir de cela, on détermine l'équation de la droite (AB) ... fais-le ( tu devrais trouver : y = ((m-3)/2) * x + m ) Ensuite pour trouver une relation donnant l'abscisse d"un point d'intersection de la parabole et de la droite (AB), il suffit d'éliminer y dans le système : y = (m-3)/2 * x + m y = x² - 3x + 2 Et tu devrais alors trouver la relation donnée dans l'énoncé (soit : 2x² - (m+3).x + 4 - 2m = 0) ***** 2) suivre les instructions de l'énoncé ... Il faut ensuite faire un tableau de signe de (m² + 22m - 23) (quand m varie) ... et en tirer les conclusions. ***** Quand tu auras fait tout cela, envoie ce que tu auras trouvé sur le site et il y aura bien un ou l'autre pour te corriger si c'est nécessaire.

Bonjour, En mesurant au mieux (ou plutôt au moins mal), j'arrive à ceci : Sans titre.bmp Mais, les mesures sur un écran avec une latte graduée ne sont pas très précises. Et mon résultat est peut-être "chanceux." Il semble que mon image ne passe pas, elle est aussi sur ce lien :

Bonjour, Attention que pour la question 3 ... il faut tenir compte que le nombre de 5 chiffres ne peut pas commencer par 0 (même si ce n'est pas écrit explicitement dans l'énoncé)

Bonjour. Calcule U(n+1) - U(n) ... tu devrais pouvoir montrer que c'est égal à (n²+n+2)/2 ... qui est un nombre entier naturel car : (n²+n+2)/2 = n(n+1)/2 + 1 Or n(n+1) est le produit de 2 entiers consécutifs et donc ce produit est toujours pair. --> n(n+1)/2 est un entier 0 et (n²+n+2)/2 aussi. On a donc U(n+1) = U(n) + 1 nombre entier (>= 0) Donc si U(n) est un nombre entier naturel, U(n+1) est aussi un nombre entier naturel (1) ***** Comme tu as montré que U(0) = 0 est donc un entier naturel ... par (1), on a que U(n) est nombre entier naturel pour tout n de N.

Rebonjour, Ex 3 - Il faut commencer par vérifier avec les cotes fournies dans l'énoncé que le triangle ACB est rectangle en C (Pythagore) - Si c'est vérifié (que le triangle ACB est rectangle en C), alors on calcule l'angle demandé en utilisant la relation (que tu dois avoir apprise) : BC = AB.sin(BAC) ***************** Ex 4 Il suffit de suivre les consignes de l'énoncé. La seule petite difficulté est qu'il faut prendre garde aux unités (ne pas mélanger des mm et des m ou ...) ***************** Tu peux envoyer ce que tu auras réalisé comme travail sur le site. Il y aura bien un ou l'autre pour t'aider à corriger si c'est nécessaire. Ce n'est pas une option de dire que tu n'arrives à rien faire ... Essaie et montre ce que tu as fait.

Bonjour, L'énoncé de l'exercice 2 aurait pu être plus précis. Je suppose qu'on doit deviner que la partie centrale est cylindrique et que les 2 extrémités sont des demi sphères. Avec les cotes sur le dessin, on peut déduire que le cylindre central a un rayon de base de 0,4 m et une hauteur de 2 - 0,8 = 1,2 m (il faut déjà comprendre cela) On peut alors calculer le volume de ce cylindre. Les 2 parties des extrémités ont un volume total égal à celui d'une sphère de rayon 0,4 m ... on peut donc calculer le volume de ces parties. La volume total est la somme des volumes calculés ci-dessus. (c'est le volume extérieur bien entendu ... mais il faut encore supposer que l'épaisseur des tôles est quasi nulle, et que donc le volume intérieur est pratiquement égal au volume calculé ... qu'on devra exprimer en litres pour répondre à la question 2.

Bonjour, [xVx - 1 + (x-1)V(x-1)]/V(x²-1) = (xVx - 1)/(V(x-1).V(x+1)) + (x-1).V(x-1)/(V(x-1).V(x+1)) = (xVx - 1). (xVx + 1)/(V(x-1).V(x+1).(xVx + 1)) + (x-1)/V(x+1) = (x³-1)/(V(x-1).V(x+1).(xVx + 1)) + (x-1)/V(x+1) = (x-1)(x²+x+1)/(V(x-1).V(x+1).(xVx + 1)) + (x-1)/V(x+1) = V(x-1) * (x²+x+1)/(V(x+1).(xVx + 1)) + (x-1)/V(x+1) Et la lim pour x--> 1+ = 0 * 3/(V2 * 2) + 0/V2 = 0 + 0 = 0 Désolé pour l'écriture ... vivement Latex sur le site.