Black Jack

Bonjour, Il y a une autre manière d'aborder l'exercice ... qui donne un résultat différent. Voila cette autre manière : Au départ, on a l'équivalent de 280 + 20 = 300 g d'eau à 16°C On attend 10 min pendant lesquelles, le température descend de 10*0,1 = 1 °C A ce moment, on a donc l'équivalent de 300 g d'eau à 16-1 = 15 °C On ajoute sur 32 min une masse M d'eau à 20 °C ... et la température finale est 16,8°C. Mais pendant les 2 minutes, il y a eu un refroidissement de 2*0,1 = 0,2 °C Et donc sans ce refroidissement, la température finale aurait été de 16,8 + 0,2 = 17 °C On peut donc considérer que, si on n' avait pas ce refroidissement, juste avant l'ajout de la masse M (en grammes) d'eau, on aurait eu 300 g d'eau à 15°C et après ajout de l'eau, on aurait (300 + M) grammes d'eau à 17 °C On a donc : 300 * 15 + M * 20 = (M + 300)*17 ...qui donne M = 200 g **************** Par la méthode donnée au début, on aurait trouvé : 300 * 16 + M * 20 = (M + 300) * 18 ... qui donne M = 300 g **************** Pas très satisfaisant d'avoir 2 réponses (très) différentes suivant le raisonnement fait. Je laisse ouverte la discussion sur le sujet à celui qui le désire. Je me contente de mentionner que cet exercice n'est pas le moins du monde réaliste et que c'est une des raisons qui peut amener des raisonnements différents... et des réponses différentes aussi. Un calorimètre qui se refroidirait à une telle "vitesse" est impensable sauf si il était dans un ambiance extrêmement froide. De plus, même dans ce cas, la vitesse de refroidissement ne peut pas être constante avec le temps et doit également varier à cause de l'ajout de l'eau, puisqu'on modifie alors assez fortement la capacité thermique massique de l'ensemble calorimètre + eau sans modifier beaucoup la résistance thermique de l'ensemble vers l'ambiance (et donc cela doit modifier la constante de temps de refroidissement) Bref, j'attends les réactions éventuelles sur cet exercice ... si il y a des volontaires.

La valeur en eau du calorimètre est de 20 grammes ... Cela signifie que, thermiquement, le calorimètre se comporte comme 20 g d'eau. Donc un calorimètre de valeur en eau 20 g contenant 280 g d'eau, cet ensemble (eau + calorimètre) se comporte thermiquement comme 300 g d'eau seule. Donc, au départ , on a un calorimètre de valeur en eau 20 g contenant 280 g d'eau, le tout à 16°C ... Et cet ensemble se comporte comme 280+20 = 300 g d'eau à 16°C. Donc au départ (avant de verser l'eau supplémentaire), on est équivalent à 300 g d'eau à 16°C ---- On verse en plus une masse M(en grammes) d'eau, on a alors au final l'équivalent de 280 + 20 + M = 300 + M grammes d'eau (et ceci tient compte du calorimètre) Cette masse totale se retrouve au final à 16,8 °C MAIS il faut tenir compte que cette température de 16,8 °C a été obtenue avec un refroidissement (perte de chaleur vers l'ambiance). La durée de refroidissement est de 10 minutes (voir énoncé par la phrase "Après 10 min de fonction...) augmentée de 2 minutes (voir énoncé par la phrase "On verse un filet d'eau pendant 2 minutes). Donc la durée totale de refroidissement est 10 + 2 = 12 minutes. Comme le refroidissement est de 0,1 °C/min, le refroidissement total a été de 0,1 * 12 = 1,2 °C Donc si il n'y avait pas eu de refroidissement, la température finale aurait été 16,8 + 1,2 ° = 18 °C ----- Donc tout se passe comme si, on n'avait pas de refroidissement et qu'on partait de 300 g d'eau à 16°C pour au final avoir une masse d'eau de (300+M) grammes à 18 °C ----- Tu peux donc calculer la masse M d'eau ajoutée comme si on n'avait pas de refroidissement et qu'on partait de 300 g d'eau à 16°C pour au final avoir une masse d'eau de (300+M) grammes à 18 °C

Bonjour, Si la vitesse de refroidissement est constante sur toute la durée de l'exercice, comme c'est indiqué dans l'énoncé (bien que cela ne peut pas être correct). ... alors sur les 10 + 2 = 12 minutes que dure l'exercice, le refroidissement a été de 0,1 * 12 = 1,2 °C Si il n'y avait pas eu ce refroidissement, la température finale aurait été 16,8 + 1,2 = 18 °C On peut donc calculer la quantité d'eau ajoutée pendant les 10 minutes en faisant comme si il n'y avait pas de refroidissement et qu'on partait de 280 + 20 = 300 g d'eau à 16°C (cela tient compte de la valeur en eau du calorimètre) ... et qu'on ajoutait une masse M (en grammes) d'eau à 20 °C et que le résultat final était une masse (300 + M) grammes d'eau à 18 °C ... Le calcul est alors évident et devrait amener à une masse d'eau ajoutée M = 300 g

Bonjour, Cela, c'est beaucoup moins sûr. Le diplôme est une chose, la compétence en est une autre.

Bonjour, Je n'ai pas vérifié tes équations initiales de B et R ... Si elles sont exactes, il est possible de les simplifier plus que tu ne l'as fait. On arrive au final à : B = b.c.d + a.b.c R = c(barre) + b(barre)

Bonjour, 1) Les protons ont une charge positive ... ils sont donc attirés par la plaque négative et repoussé par la plaque positive. Et donc l'armature reliée à la borne positive est ... 2) E = U/L = ... V/m 524934 V/m F = q * E (et la charge q d'un proton est e = 1,60.10^-19 C --> F = ... N (8,40.10^-14) 4) a(t) = F/m = e*E/m = e * U/(m*L) v(t) = a(t) * t = e * U/(m*L) * t x(t) = a(t) * t²/2 = e * U/(2*m*L) * t² 5) Vitesse max atteinte lorsque les protons arrivent en B, donc à l'instant t1 tel que x(t1) = L L = e * U/(2*m*L) * t1² t1² = 2*m*L²/(e*U) t1 = RacineCarrée[2*m*L²/(e*U)] v(t1) = e * U/(m*L) * RacineCarrée[2*m*L²/(e*U)] vB = v(t1) = RacineCarrée[2*e*U/m] (indépendant de la longueur L) 6) F = E * e = U/L * e W(F sur L) = F * L W(F sur L) = U/L * e * L W(F sur L) = U * e 7) Le travail de la force électrostatique sur la distance L = énergie cinétique du photon e * E * L = 1/2 . m . vB² vB² = 2qEL/m Or E = U/L --> v² = 2eU/m vB = RacineCarrée[2*e*U/m] (indépendant de la longueur L) Rien relu ... vérifie et fais les calculs numériques

Bonjour, Il y a beaucoup erreurs. Par exemple : -20/4 = -5 ... et donc -20/4 est un nombre entier relatif. ********** Nombres pas décimaux : nécessitent une infinité de décimales si on essaie de les écrire sous forme décimale. Par exemple 1/3 ,n'est pas un nombre décimal car il peut s'écrire 1,33333... avec une infinité de chiffres derrière la virgule Autre exemple 2/7 = 0,285714285717... la suite 275814 dans les décimales se répète à l'infini et donc 2/7 n'est pas un nombre décimal. Les nombres non décimaux dans la liste sont : -35/3 et 82/11 car ... Tous les autres nombres de la liste sont des nombres décimaux. (exemple -15/-6 = 2,5 ... est donc décimal) ********** Un nombre rationnel est, un nombre qui peut s'exprimer comme le quotient de deux entiers relatifs. Chacun des nombres de la liste peut se mettre sous la forme d'un quotient de deux entiers relatifs ... même 3 qui peut s'écrire 3/1 ou 6/2 ou ...

Remis à l'endroit ... mais pas plus clair ...

Bonjour, "sqrt" pour Racine carrée. (abréviation venant de l'anglais : Square root) On sait que c'est un cône ... parce que l'énoncé l'a précisé. Mais, même si cela n'avait pas été écrit dans l'énoncé, on pouvait le savoir, puisque on a montré que l'angle alpha est une constante et que donc ...

Bonjour, 1) x(t) = e^t * sin(t) y(t) = e^t * cos(t) z(t) = e^t calcul des composantes de la vitesse suivant les 3 axes du repère : vx(t) = dx/dt = e^t * (cos(t) + sin(t)) vy(t) = dy/dt = e^t * (cos(t) - sin(t)) vz(t) = dz/dt = e^x |v| = sqrt((vx)² + (vy)² + (vz)²) |v| = sqrt[(e^t * (cos(t) + sin(t)))² + (e^t * (cos(t) - sin(t)))² + (e^t)²] |v| = e^t * sqrt[(cos(t) + sin(t))² + (cos(t) - sin(t))² + 1] |v| = e^t * sqrt[cos²(t) + sin²(t) + 2.sin(t).cos(t) + cos²(t) + sin²(t) - 2.sin(t).cos(t) + 1] |v| = e^t * sqrt[3] **** Pour l'accélération ... calcul des composantes de l'accélération suivant les 3 axes du repère : on calcule ax(t) = d(vx)/dt = ... ay(t) = d(vy)/dt = ... az(t) = d(vz)/dt = ... Et |a| = sqrt((ax)² + (ay)² + (az)²) = ... **** 2) O(0 ; 0 ; 0) M(e^t * sin(t) ; e^t * cos(t) ; e^t) vect(OM) = (e^t * sin(t) ; e^t * cos(t) ; e^t) vect(uz) = (0 ; 0 ; 1) vect(OM).vect(uz) = e^t * sin(t) * 0 + e^t * cos(t) * 0 + e^t * 1 = e^t |OM| = sqrt[(e^t * sin(t))² + (e^t * cos(t))² + (e^t)²] = e^t * sqrt(2) |uz| = 1 vect(OM).vect(uz) = |OM| * |uz| * cos(alpha) e^t = e^t * sqrt(2) * cos(alpha) cos(alpha) = 1/sqrt(2) alpha = Pi/4 ***** rien relu et donc ... toutes erreurs incluses.

Bonjour, Il y a un soucis, je pense, avec la relation P1=P0+2 Quand on met le poids de 2 kgf sur le piston, la pression dans le cylindre augmente de 2 kgf/S, avec S la section du piston en cm² Or S = 0,2 dm², soit 20 cm² --> la pression dans le cylindre augmente de 2/20 = 0,1 kgf/cm² Et donc P1 = P0 + 0,1 (en kgf/cm²) P0 étant la pression dans le cylindre avant de mettre le poids de 2 kgf en place (donc P0 = Patmos + Poids du piston/S = 1 + 4/20 = 1,2 kgf/cm²) ... Sauf distraction.

Merci, je m'associe aux voeux de bonne année et bonne santé pour tous.

Bonjour, f(x) = a.x² + bx + c f '(x) = 2a.x + b Et on mesure sur le graphique (à comprendre) : a) f '(2) = 1 b) f(2) = 5 c) f(0) = 1 A partir de là, tu peux écrire un système de 3 équations à 3 inconnues (a, b et c) Et en résolvant ce système, tu trouveras les valeurs de a, b et c ...

Bonjour, Je présume que ABCDEFGH est un cube ... mais cela DOIT être précisé dans l'énoncé, sinon on ne peut rien conclure. Si ABCDEFGH est bien un cube, les 6 faces du cubes sont identiques, ce sont des carrés. Les diagonales de carrés identiques sont égales. DE est la diagonale d'un coté du cube, DB est la diagonale d'un coté du cube Et donc ... Si on appelle L la longueur d'une arête du cube, on a DE = DB = L * RacineCarrée(2)

Bonjour, Rien ne dit d'ailleurs qu'il est impossible d'avoir à partir d'un même code plusieurs messages différents intelligibles.

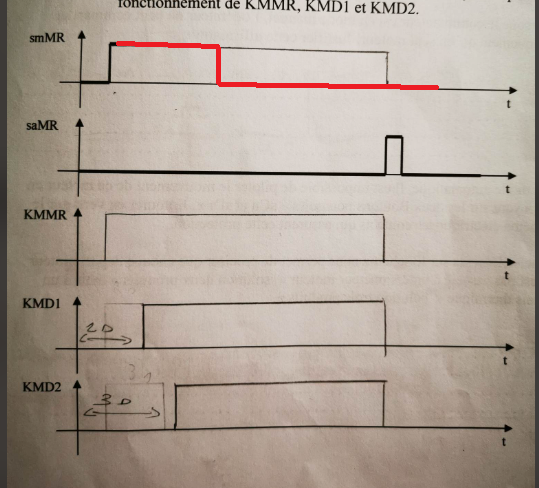
Bonjour, Questions 4 et 6 Voir dessin corrigé. Le rôle principal de Ka2 est de maintenir la tension sur LMMr. Lorsqu'on pousse sur le bouton poussoir SmMR, KMD1 s'enclenche après une temporisation et après une seconde temporisation, KMD2 s'enclenche. Un contact de KMD2 (33-34)enclenche Ka2 ... Et le contact 33-34 de Ka2 shunte le bouton poussoir SmMR, on peut alors relacher le bouton poussoir SmMR, le circuit reste sous tension via le contact mentionné de Ka2 Donc Ka2 est le relais de maintien sous tension de cette partie de circuit. On se sert, d'un contact de Ka2 pour allumer un voyant H2 (ceci n'a qu'une fonction de signalisation). Le rôle majeur de Ka2 est bien de maintenir la tension sur le circuit des relais KMMr, KMD1 et KMD2 lorsqu'on relache le bouton poussoir SmMr.

Bonjour, KA1 est le contacteur de mise sous tension de l'entièreté du circuitde commande. A la mise sous tension entre les bornes de gauche du schéma, la bobine de KA1 n'est pas alimentée. Le contact KA1(53-54) est ouvert et tout le circuit qui suit n'est pas alimenté. Si on pousse sur le bouton poussoir Sma, on alimente la bobine de KA1. Le contact KA1(33-34) se ferme et maintient KA1 enclenché même quand on relache le bouton poussoir Sma. Le contact KA1(53-54) est maintenant fermé et permet l'alimentation de tout le circuit de commande. Pour arrêter, on pousse sur le Bouton poussoir Sat qui fait retomber le contacteur KA1 qui coupe (par son contact 53-54) l'alimentation sur tout le circuit de commande. KA1 est donc le contacteur de "marche - arrêt" de l'ensemble du circuit de commande.

Bonjour, Quelques mots pour différencier les contacteurs KA et les contacteurs KM sur ce lien : http://www.mytopschool.net/mysti2d/activites/polynesie2/ETT/C041/32/DemarrageMoteur2/files/Documents/TECH22_Contacteur.pdf Dans le schéma, on distingue aussi des contacteurs instantanés (au temps de réaction près) et d'autres temporisés (mais je ne sais pas ce qui est demandé) Quelques explications sur ce lien : https://knowledge.autodesk.com/fr/support/autocad-electrical/learn-explore/caas/CloudHelp/cloudhelp/2019/FRA/AutoCAD-Electrical/files/GUID-DA927086-EEAF-48CB-B9B1-634A4B48C8C7-htm.html

Bonjour, Cela aurait peut-être été un peu plus clair ainsi ?

Bonjour, Suggestion (mais je ne suis pas matheux et donc méfiance ...) 1c) A partir du résultat de 1b. Posons U(k) = x^(k+1)/((n+1)!) On a alors U(k+1) = x^(k+2)/((k+2)!) U(k+1)/U(k) = x/(k+2) Donc U(k+1)/U(k) < 1 pour k > x - 2 La suite Uk est donc décroissante pour k > x - 2 x^(n+1)/((n+1)!) * e^x < x^(ent(x))/(ent(x)!) * e^x **** U(n+1)/U(n) < 1 (pour n ent(x) - 1) Les termes de Un sont inférieurs (à partir du rang n = ent(x) - 1) à ceux d'une suite géométrique de raison = 1 - epsilon (epsilon petit mais > 0) ... et donc lim(n--> +oo) U(n) = 0 Sauf si je me suis égaré.

Bonjour, Je pense qu'il y a une erreur d'énoncé. Pour la question 4, l'intégrale à considérer devrait avec la borne inférieure = 3 et par = 1 Avec cette modification, on a, pour tout n 3, Un > intégrale ... et on peut alors conclure.

Bonjour, Partie 2 3) a) Coordonnées de Amiens : (0 ; 4) Coordonnées de Nancy : (7,6 ; 0) distance Amiens Nancy = racineCarrée[(7,6-0)² + (4-0)²] = 8,59 unités de longueur. Or par l'échelle (en bas à droite de la carte), on sait que 4 unités de longueur représentent 150 km ---> Distance (en km) Amiens Nancy = 8,59/4 * 150 = 322 km (à vol d'oiseau) ******** b) Autrement : On mesure sur la carte à la règle graduée la distance Amiens Nancy (ligne en rouge sur le dessin) : soit L1 mm cette longueur sur la carte On mesure sur la carte à la règle graduée la distance représentant 150 km en bas à droite de la carte (ligne en jaune sur le dessin): soit L2 mm cette longueur sur la carte La distance Amiens Nancy (en km) est : 150 * L1/L2 ... (et on devrait retrouver une distance proche de celle trouvée par la méthode a) ******** Pour les questions 1-2 de la partie 2 ... on utilise une des méthodes comme montré ci-dessus.

Bonjour, La moindre des choses est d'essayer d'avancer un peu par soi-même ... et ne pas oublier au minimum, un bonjour ou ... 1) U1 = 0 Pour n dans [1 ; 10], on a U(n) = U1 + (n-1)*r, soit donc U(n) = (n-1)*r (suite arithmétique) --> U(10) = 9*r U(16) = U(10) * q^6 (suite géométrique) -1/27 = 9*r * q^6 r*q^6 = -1/(27*9) = -1/243 r*q*q^5 = -1/243 q^5 = -1/243 q = -1/3 r = 1/q = -3 U(10) = 9*r = 9*(-3) = -27 U(11) = U(10) * q = -27 * (-1/3) = 9 2) Le calcul de Sn est facile ... si on connait les relations donnant la somme de termes en progression arithmétique et la somme de termes en progression géométrique. Il faut évidemment distinguer le cas avec n 10 du cas avec n > 10 ...

Bonjour, Encore un énoncé litigieux. Pour remplir le tableau comme l'a fait PAVE (progression arithmétique), il faut aller chercher une information qui est absente de la partie 1 de l'énoncé. L'info de "progression arithmétique" peut être tirée de la partie 2 ... mais n'est en aucun cas présente dans la partie 1 de l'énoncé. Donc si on s'attaque au problème en suivant les points de l'énoncé dans l'ordre, l'info "progression arithmétique" n'est pas connue au moment de remplir le tableau. On peut donc imaginer n'importe quel algorithme qui respecte évidemment les quelques cases imposées du tableau En voila par exemple un autre dans lequel on aurait choisi une progression géométrique (raison = 11,5^(1/7)) On pourrait aussi utiliser une infinité d'autres algorithmes qui satisferaient parfaitement la partie 1 de l'énoncé. ***** C'est évidemment quasi sûr que c'est la "progression arithmétique" qui est attendue ... mais il n'empêche que l'énoncé, tel que rédigé, ouvre la porte à n'importe quelle autre progression (géométrique ou autre)

Bonjour, Un petit dessin ... et tout est évident ...