Black Jack

Bonjour, On a une charge uniformément répartie de 70 daN/m sur la poutre de 10 m On peut l'assimiler à une force verticale vers le bas de 70 * 10 = 700 daN appliquée au milieu de la poutre ... soit donc à 5 m de D et 1 m de C (sur le segment [CD]) Au total, on a donc l'équivalent de : F1 = 130 daN (il manque l'unité sur ton dessin) verticale vers le bas à l'extrémité gauche de la poutre. F2 = 700 daN verticale bers le bas appliquée au milieu de la poutre. Les réactions RC et RD des appuis sur la poutre (verticales vers le haut) Comme la poutre est immobile, la somme vectorielle de toutes les forces sur la poutre est nulle. Et comme F1, F2, RC et RD sont verticales, on a en tenant compte du sens des forces : RC + RD - F1 - F2 = 0 --> RC + RD = 130 + 700 = 830 daN (1) La poutre est immobile et donc ne pivote pas autour de D --> la somme des moments autour du point D des forces agissant sur la poutre est nulle. Ceci permet d'écrire : F1 * (4 + 6) + F2 * 5 - RC * 6 = 0 (2) 130 * 10 + 700 * 5 = 6.RC RC = 800 daN et avec (1) --> RD = 830 - 800 = 30 daN *********** Remarque, au lieu de calculer RC par lé relation (2), on aurait pu calculer RD en exprimant que la somme des moments autour du point C des forces agissant sur la poutre est nulle. On aurait eu alors : F1 * 4 - F2 * 1 + RD * 6 = 0 130*4 - 700*1 + 6.RD = 0 RD = 30 daN Et en déduire RC par (1) --> RC = 830 - 30 = 800 daN On arrive évidemment aux mêmes résultats. *********** Autre remarque : Ici, on trouve bien RC et RD > 0 (donc dirigés vers le haut). Si on avait trouvé par exemple RD < 0 (cela aurait été impossible, car un appui ne peut pas "retenir" la poutre) ... Cela aurait signifié que la poutre ne pouvait pas rester en équilibre, elle aurait pivoté autour du point C. Cela serait le cas, par exemple, si la force F1 était considérablement > 130 daN ***********

Bonjour, Les dessins ne correspondent pas aux exercices écrits. Je reprends le dessin 11 qui correspond à ta résolution 12 ... qui n'est pas correcte. Les 90 daN/m répartis sont équivalents en statique à 513 daN au milieu de la poutre, donc au dessin que j'ai redessiné en dessous. Avec RA et RB verticales vers le haut, on a : RA+RB = 150 + 513 = 663 daN La somme des moments des forces autours A est nulle et donc : 513 * 0,95 - RB*3,8 = 0 RB = 128,25 daN et RA = 663 - 128,25 = 534,75 daN Ce qui n'a rien à voir avec ce que tu as trouvé. ********** Essaie de comprendre et refaire le tout ... même les autres exercices.

Bonjour, Ex1 1.1 f(x) = Ax² - Bx + B - A Delta = (-B)² - 4A*(B-A) Delta = B² + 4A² - 4AB Delta = (B - 2A)² (forcément 0) f(x) = 0 pour x = [B +/- (B - 2A)]/(2A) donc pour x1 = 1 et x2 = (B - A)/A Ax² - Bx + B - A = A.(x-1).(x - (B-A)/A) ou si on préfère : Ax² - Bx + B - A = (x-1).(A.x + A - B) Remplacer A et B par leurs valeurs numériques (conformément à l'exercice 0) ...

Pour être un peu plus rigoureux, j'aurais du écrire : Et pour les questions du début ... Revoir la "règle du tire-bouchon" et la "règle des 3 doigts de la main droite"

Bonjour, Et pour les questions du début ... Revoir la "loi du tire-bouchon" et la "loi de la main droite"

Bonjour, Avec RA et RB verticales vers le haut : RA + RB = F1 + F2 + F3 RA + RB = 3000 + 4000 + 200 = 7200 N La somme des moments des forces autour de B est nul et donc: RA * 4 - F1 * 3,2 - F2 * 1,6 + F3 * 1 = 0 4.RA - 3000*3,2 - 4000*1,6 + 200*1 = 0 RA = 3950 N (vertical vers le haut) RB = 7200 - 3950 = 3250 N (vertical vers le haut)

Bonjour, Je présume qu'il s'agit d'un "service", sinon les explications ne tiendraient pas la route. En prenant le pied du filet comme origine O du repère, l'axe vertical (ordonnées), et l'axe des abscisses horizontal dans le plan de la trajectoire ... Avec f(x) la trajectoire du point le plus bas de la boule : f(x) = ax² + bx + c f'(x) = 2ax + b f(-120) = 0 f(-45) = 27-2 = 25 (comprendre le pourquoi du (-2)) f'(-45) = 0 (car au sommet de la trajectoire, la tangente à la trajectoire est horizontale) 0n obtient donc le système suivant qu'il faut résoudre : a(-120)² - 120.b + c = 0 a*(-45)² - 45.b + c = 25 2*a*(-45) + b = 0 Tu devrais trouver : a = -0,0044444... b = -0,4 c = 16 f(x) = -0,0044444... x² - 0,4 x + 16 Au niveau du filet (abscisse x = 0), le bas de la balle passe donc à une hauteur f(0) = 16 (cm) Et donc ...

g(x) croît pour x entre moins l'infini et a g(x) décroît pour x entre a et l'infini

Bonjour, f(x) = 2x + 3 - e^x f'(x) = 2 - e^x f(a) = 2a + 3 - e^a f'(a) = 2 - e^a Ceci permet de trouver l'équation de la tangente à la courbe représentant f(x) au point d'abscisse a. Tu devrais trouver : Ta : y = (2-e^a).x + (a-1).e^a + 3 *** La courbe représentant f(x) sera en dessous de toutes ses tangentes, si pour tout a de R, on a : f(x) - ((2-e^a).x + (a-1).e^a + 3) 0 (le = aux points de tangence) Il te faut donc démontrer que : 2x + 3 - e^x - ((2-e^a).x + (a-1).e^a + 3) 0 pour tout a de R. soit g(x) = 2x + 3 - e^x - ((2-e^a).x + (a-1).e^a + 3) Tu étudies les variations de la fonction g g'(x) = ... signe de g'(x) ... Et tu devrais pouvoir conclure que g est minimum pour x = a et que ce minimum vaut g(a) = - e^a + e^a * a - a.e^a + e^a = 0 ... Et que donc 2x + 3 - e^x - ((2-e^a).x + (a-1).e^a + 3) 0 pour tout a de R. Et pouvoir conclure que la courbe représentant f(x) est en dessous de toutes ses tangentes.

Bonjour, Pas besoin de calculette pour résoudre cette équation : Avec un poil de réflexion ... Poser (1+t)^-1 = x (avec x différent de 0) L'équation devient : 2120x + 2500x²+2970x³ = 0 A la main : x.(2970x² + 2500x + 2120) = 0 ... x = 0 ... qui ne convient pas. Si on veut les autres solutions (complexes), alors : 2970x² + 2500x + 2120 = 0 297x² + 250x + 212 = 0 delta réduit = 125²-212*297 = -47339 x = (-125 +/- i.sqrt(47339))/297 (1+t)^-1 = (-125 +/- i.sqrt(47339))/297 1 + t = 297/(-125 +/- i.sqrt(47339)) t = -1 + 297/(-125 +/- i.sqrt(47339)) facile à remettre sous la forme t = a + i.b pour ces 2 solutions, on en arrondissant : -1,589622641509 - 1,02629846382.i -1,589622641509 + 1,02629846382.i ********* A la calculette : Après être arrivé à 2120x + 2500x²+2970x³ = 0 (voir calculs "à la main") on entre cette équation dans la calculette ... qui donne comme solutions : 0 ; -0,420875420875 - 0,732576681248.i ; 0 ; -0,420875420875 + 0,732576681248.i x = 0 est à écarter (voir dans calcul "à la main") Quand on a : x = -0,420875420875 - 0,732576681248.i On inverse la valeur (1/x) avec la calculette .... qui donne 1/x = -0,589622641509 + 1,02629846382i et 1/x valant t+1 ... on retranche 1 à ce qui a été trouvé, et on a : t = -1,589622641509 + 1,02629846382i et on a aussi -0,420875420875 + 0,732576681248.i On inverse la valeur (1/x) avec la calculette .... qui donne 1/x = -0,589622641509 -1,02629846382i et 1/x valant t+1 ... on retranche 1 à ce qui a été trouvé, et on a : t = -1,589622641509 - 1,02629846382i ********* Les solutions sont donc : t = -1,589622641509 + 1,02629846382i ou t = -1,589622641509 - 1,02629846382i

Bonjour, Qu'as-tu fait ? La plupart des questions sont des applications directes du cours. Il faut connaître parfaitement ces notions simples si on ne veut pas très vite décrocher. Ecris donc tes réponses ... et il y aura bien un ou l'autre qui t'aidera pour te corriger si nécessaire.

Bonjour, Bonjour, 2 grosses erreurs : 1)Encelade est un satellite de Saturne et donc la masse à prendre en considération, lors du calcul de la période de révolution de Encelade autour de Saturne, est celle de Saturne et pas celle de la Terre. 2) De plus, il faut utiliser des unités cohérentes ... et donc dans le SI, il faut utiliser le m et pas le km pour les distances (R = 0,238.10^9 m) GMm/d² = mw².d GM/d³ = w² GM/d³ = (2Pi/T)² GM/d³ = 4Pi²/T² T = 4Pi²*d³/(GM) Avec G = 6,67.10^-11 (SI) et M la masse de SATURNE = 5,693.10^26 kg et d la distance entre le centre de Saturne et son satellite (soit ici 0,238.*10^9 m) T² = 4*Pi²*(0,238.*10^9)³/(6,67.10^-11 * 5,693.10^26) T² = 1,402.10^10 s T = 118389 s (environ 1,37 jour terrestre)

Bonjour, Ce n'est pas vraiment mon domaine mais soit ... En négligeant les poids propres de la poutrelle, du plat en acier et du béton ... a) F = Sigma * S 50000 = 10 * S (avec S en mm²) S = 5000 mm² (50 cm²) b) F = Sigma * S 50000 = 0,4 * S (avec S en mm²) S = 125000 mm² S = c² (avec c le coté du carré) c = 354 mm c) F = Sigma * S 50000 = 2,5 * S (avec ici S en cm²) S = 20000 cm² Pi * d²/4 = 20000 (avec d le diamètre en cm) d = 160 cm Toutes erreurs incluses. ****************************** Recopier sans comprendre est inutile.

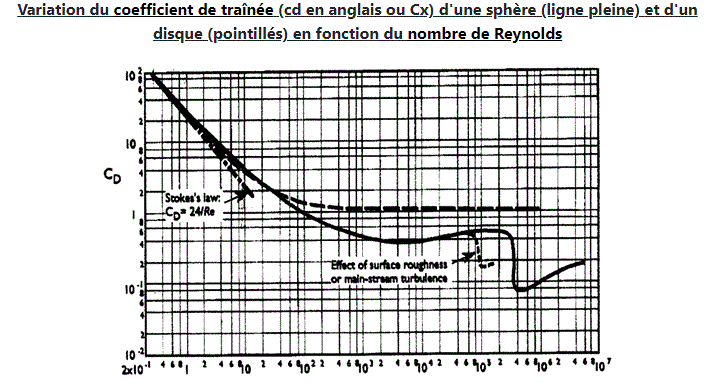
Bonjour, Ce que j'en pense, sans référence vraiment à l'énoncé qui me semble pas des plus clairs. La force de frottement est de la forme : F = 1/2 * Rho(fluide) * Cx * S * v² S est le maître couple, c'est à dire la section qui résiste au passage de l'objet dans le fluide (pour une sphère; on a S = Pi*R²) MAIS ... la valeur du Cx dépend du nombre de Reynolds (Re) et on a : Re = v * L * Rho(fluide)/µ Avec v la vitesse entre le fluide et la sphère (si on a une bille) L la longueur caractéristique de l'objet (et dans le cas d'une sphère, L = diamètre = 2R) µ est la viscosité dynamique du fluide (en Pa.s) Pour de petites valeurs de Re (nombre de Reynolds); on a Cx = 24/Re ... et dans le cas d'une sphère : Cx = 24 * µ/(v * 2R * Rho(fluide)) = 12 * µ/(v * R * Rho(fluide)) F = 1/2 * Rho(fluide) * Cx * S * v² F = 1/2 * Rho(fluide) * 12 * µ/(v * R * Rho(fluide)) * Pi*R² * v² F = 6 Pi * µ * R * v ... et nous voila retombé sur la loi de Stokes (souvent enseignée mais sans montrer d'où elle provient) ************ Pour des valeurs plus grandes de Re : On a Cx pratiquement constant (pour une sphère : Cx = 0,45 environ) On a alors la force de frottement : F = 1/2 * Rho(fluide) * Cx * S * v², avec Cx = 0,45 On appelle ce type de frottement aérodynamique (même si le fluide est un liquide) ************* On voit ce qui précède sur la courbe du Cx en fonction de Re (pour une sphère, en traits pleins). Le passage entre frottement fluide (loi de Stokes) (frottement proportionnel à v) et frottement aérodynamique (frottement proportionnel à v²) n'est évidemment pas brusque (en fonction de Re) Ce passage est sur un "arrondi" de la courbe du Cx en fonction de Re ... et si on se situe dans la zone arrondie du Cx, si on a besoin d'un peu de précision, on doit lire la valeur de Cx sur la courbe et ne pas appliquer les formules de frottement fluide ou aérodynamique ... ou on peut approcher ce qui va se passer en utilisant dans la force de frottement une partie proportionnelle à v et une autre proportionnelle à v². ************* Il y a aussi une petite difficulté supplémentaire, par le fait que pour déterminer la valeur de Re ... on a besoin de la vitesse, mais que la vitesse dépend des frottements, donc du Cx et donc de Re. (serpent qui se mord la queue). Mais avec un rien d'habitude, on arrive à renifler ce qu'on va trouver et souvent à choisir entre la courbe à frottement fluide ou aérodynamique et ... ************* Remarque, pour un nombre de Reynolds très élevé (> 10^5), il y a un "accident" dans la courbe du Cx ... mais cela dépasse probablement ce qui est attendu ici. ********** En espérant n'avoir pas embrouillé les choses encore plus fort.

Bonjour, Distraction. ATTENTION : (n-5) x 150 = n x 150 + 5x 150 devrait être (n-5) x 150 = n x 150 - 5x 150 et S1 = 5000 +150n + 750 = 5750 +150 n devrait être S1 = 5000 +150n - 750 = 4250 +150 n et 5750 + 150 x17 devrait être 4250 + 150 x17 = 6800

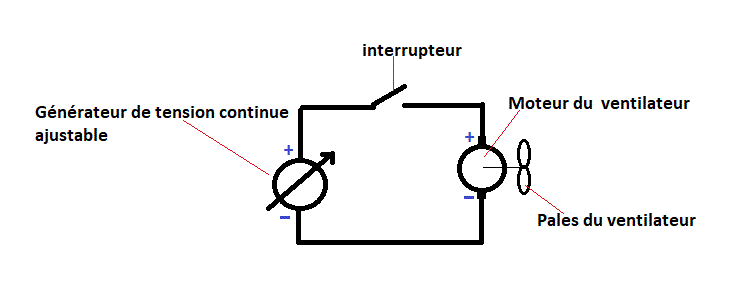
Bonjour, Protocole d'essais. - Réaliser le câblage du schéma dessiné. - Régler la tension du générateur de tension à 0 volt - Fermer l'interrupteur - Constater que le ventilateur ne tourne pas. - augmenter lentement la tension du générateur - Constater que la vitesse du ventilateur augmente lorsque on augmente la tension du générateur. Remarques : 1) Précaution à respecter : La tension maximale réglée sur le générateur de tension ne peut pas dépasser la tension nominale prévue pour le ventilateur. 2) Si on ne dispose pas d'autre matériel que celui proposé, on ne peut pas mesurer précisément la vitesse du ventilateur ... mais ce n'est pas non plus demandé. On peut se contenter de constater visuellement l'augmentation de la vitesse du ventilateur avec l'augmentation de la tension du générateur. On peut cependant, à condition de disposer d'une montre indiquant les secondes, effectuer des mesures de vitesse du ventilateur tant que la tension du générateur reste faible (en mesurant le temps mis pour effectuer 10 tours par exemple).

Bonjour, Copie d'image (ou quand cela ne fonctionne pas en fonction du type d'image, on peut faire une copie d'écran) Collage de l'image dans "Paint" (logiciel fourni de base avec la plupart des "Windows") Ajout dans "Paint" des traits nécessaires. Sauvegarder l'image en format gif ou png ou ... Insérer l'image sauvegardée sur le site. Bonne journée.

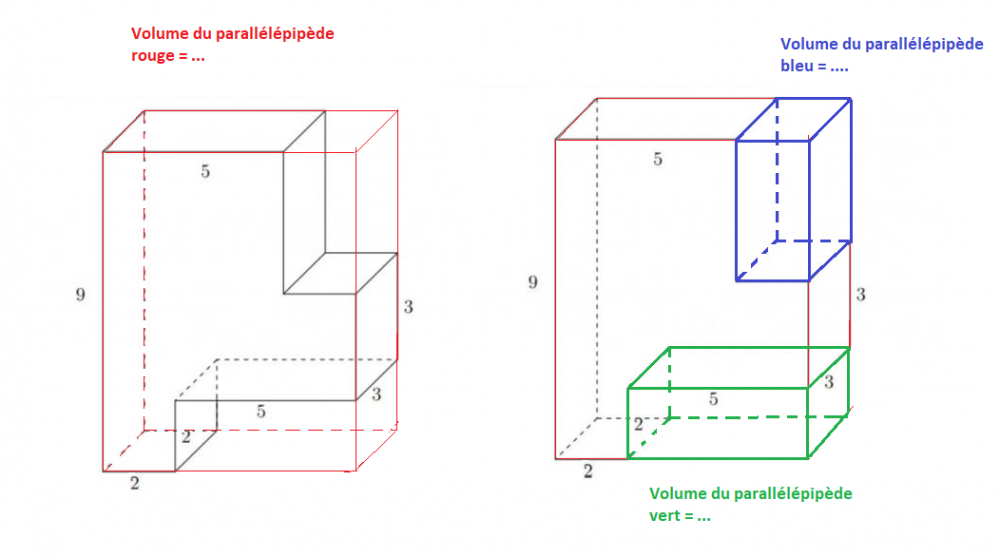
Bonjour, Alternative : Déterminer les côtes des arêtes des solides rouge, bleu et vert et calculer leurs volumes respectifs. Et puis calculer le volume demandé à partir de ceux des solides rouge, vert et bleu calculés ci-dessus.

Bonjour, Regarde sur ce lien : https://www.fondation-lamap.org/fr/page/20340/les-proprietes-inhabituelles-de-leau En comprenant ce qui y est écrit ... tu auras la réponse à ta question.

Bonjour, Partir avec (en vecteur) : AB = AC + CB (relation de Chasles) ...

Comme je l'ai écrit, la demande 5 n'est pas très explicite. J'ai proposé ce qui me semble le moins débile. Ces expressions sont plus simples avec un simple arctan(x) agrémenté d'une constante variant dans les différentes parties du domaine de définition (non connexe). Quant à l'intérêt de la chose, il est évidemment très limité ... sans savoir ce qui se passait dans la tête de celui qui a pondu l'énoncé. Si il avait en tête de tester les étudiants sur les dangers des primitives avec des fonctions définies dans des domaines non connexes, alors cela a tout son sens , mais de la manière dont la question est posée, l'intention est tellement bien cachée que cela devient plus de la divination qu'autre chose. **** Si l'idée est bien celle mentionnée ci-dessus, alors ... Pour le calcul de f(0) ... cela peut-être parce que : A partir de f'(x) = 1/(1+x²), cela saute aux yeux (ou devrait) que en "primitivant", on arrive à f(x) = arctan(x) + K et demander de calculer f(0) doit servir à trouver la valeur de K dans la partie du domaine de définition comprenant x = 0, soit dans ]-1 ; 1[ ... et par là faire penser que K doit aussi être calculé pour les autres parties du domaine de définition non connexe. Ce devrait être un réflexe pour les étudiants en supérieur (constantes différentes dans les différentes parties d'un domaine non connexe). Ceci dit, je suis peut-être (ou pas) à 100 lieues de la motivation de l'auteur de l'énoncé.

Bonjour, Peut-être que ce qui est attendu pour la question 5 (qui n'est pas très explicite) est ceci : f(x) = 2*arctan(x) + Pi pour x dans ]-oo ; -1[ f(x) = 2*arctan(x) pour x dans ]-1 ; 1[ f(x) = 2*arctan(x) - Pi pour x dans ]1 ; +oo[

Bonjour, Pour te corriger ... il faudrait commencer par écrire ce que tu as fait. 1) On connait l'effectif total : 250 On connait les effectifs pour 5 des 6 catégories, soit 12 ; 30 ; 40 ; 26 et 23 La case des effectifs non remplie est donc = 250 - (12 + 30 + 40 + 26 + 23) = ... 2) Il y a 23 hommes ayant une taille 180 cm (1,8 m) Cela représente donc 100 * 23/250 = 9,2 % des hommes. ********* Continue et écris ce que tu trouves sur le site, il y a aura bien un ou l'autre tour t'aider à corriger si besoin est.

Fiche 1 3.3 faux ***** doc 2: 3° : Non 4° : Oui 5° : Un ion 8° : C ***** Fiche 2 doc 2 : 3° : Non 4° : Oui 5° : Un ion 8° : C ******** Pour répondre aux questions 6°, il faut tenir compte de ce qui suit : la borne (-) d'une pile correspond à l'anode où se produit la réaction d'oxydation qui va fournir les électrons. la borne (+) d'une pile correspond à la cathode où se produit la réaction de réduction qui va consommer les électrons. Je te laisse choisir les réponses, moi je me trompe 1 fois sur 2 . La chimie et moi, cela fait deux. :-) ********

Bonjour, Tu confonds "masse molaire d'un produit" et "masse d'un produit" et tu confonds "masse molaire d'un réactif" et "masse d'un réactif" La masse molaire du propane est 44 g par mol Mais dans la réaction donnée de combustion, il y a 1 mol de propane, donc la masse du réactif propane dans la réaction est 1 * 44 = 44 g La masse molaire du dioxygène est 32 g par mol Mais dans la réaction donnée de combustion, il y a 5 mol de dioxygène, donc la masse du réactif dioxygène dans la réaction est 5 * 32 = 160 g La somme des masses des REACTIFS dans l'équation de combustion donnée est donc 44 + 160 = 204 g **** La masse molaire du dioxyde de carbone est 44 g par mol Mais dans la réaction donnée de combustion, il y a 3 mol de dioxyde de carbone, donc la masse du produit dioxyde de carbone dans la réaction est 3 * 44 = 132 g La masse molaire de l'eau est 18 g par mol Mais dans la réaction donnée de combustion, il y a 4 mol d'eau, donc la masse du produit eau dans la réaction est 4 * 18 = 72 g La somme des masses des PRODUITS dans l'équation de combustion donnée est donc 132 + 72 = 204 g **** On a donc bien "somme des masses des réactifs" = "somme des masses des produits" = 204 g ************* Ta confusion est similaire par exemple en se trompant entre la masse d'une pomme et la masse des pommes qu'il y a dans mon panier. La masse d'une pomme est 100 g, par exemple (équivalent à la masse molaire dans le problème de chimie), mais si j'ai 5 pommes dans mon panier ... la masse des pommes dans mon panier est 5 kg (équivalent à la masse du PRODUIT (ou du réactif) dans le problème de chimie) Et si dans mon panier, j'ai des pommes et des poires, la masse de fruits dans mon panier est la somme des masses de toutes les pommes et de toutes les poires ... et pas la somme de la masse d'une poire et la masse d'une pomme. OK ?