Black Jack

Bonjour, Exercice 1 J'utilise les données de l'énoncé (bien que la donnée pour le champ magnétique de la Terre est complètement faux) (La valeur du champ magnétique pour une étoile à neutrons donnée par l'énoncé est du bon ordre de grandeur) 1) Julie se trompe, on n'a évidemment pas 5.10^-2 T proche de 10^8 T et donc ... 2) Champ magnétique étoile / champ magnétique Terre = 10^8/(5.10^-2) = 2.10^9 3) Le champ magnétique d'une étoile à neutron est 2 milliards de fois plus fort que celui de la Terre. (évidemment faux vu ma remarque sur l'erreur de l'énoncé sur la valeur du champ magnétique terrestre. **********************

Bonjour, Sacrenom, Le champ magnétique terrestre est 5.10^-2 T Et puis quoi encore ? Piqué sur le net : Intensité du champ magnétique terrestre Le champ magnétique terrestre varie au cours du temps. Actuellement, son intensité décroît ; à la surface de la Terre, celle-ci est comprise entre 33.000 et 70.000 nT (nanotesla). Au centre de la France, il est d'environ 47 µT (microTesla) ***************** La donnée de l'énoncé sur la valeur du champ magnétique terrestre n'est jamais qu'un facteur 1000 à coté de la réalité ... une paille. Et on voudrait avec de telles "énormités" que les élèves (étudiants) acquièrent un bon feeling. 😒

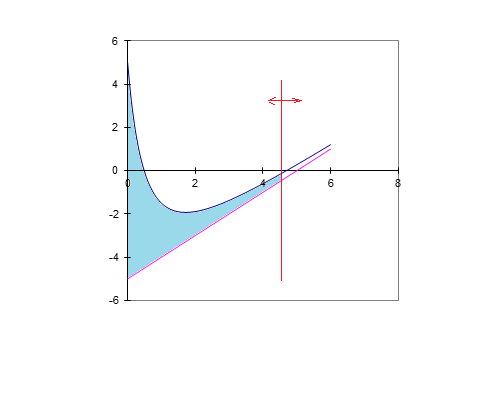
\(A_p = \int_0^p \frac{10}{(x+1)^2} dx\) \(A_p = -10.[\frac{1}{x+1}]_0^p \) \(A_p = -10*[\frac{1}{p+1} - \frac{1}{1}] \) \(A_p = -10*\frac{1-(p+1)}{p+1}\)\(\) \(A_p = \frac{10.p}{p+1}\)

Bonjour, Voir image sur ce lien : https://zupimages.net/up/21/18/lrss.png 3) a) Ap = S(de 0 à p) (f(x) - g(x)) dx Ap = S(de 0 à p) 10/(x+1)² dx ********* b) Ap = S(de 0 à p) 10/(x+1)² dx Ap = [-10/(x+1)](de 0 à p) Ap = -10/(p+1) + 10 Ap = 10.(1 - 1/(p+1)) Ap = 10.p/(p+1) ********* c) lim(p--> +oo) Ap = 10

Bonjour, 2c) f2 est décroissante sur [0 ; +oo[ (par 2b) f2(0) = 1 - 0 - cos(0) = 0 Des 2 lignes précédentes, on peut dire que f2(x) 0 sur [0 ; +oo[ et donc ... ****** Présentation à arranger avec les "habitudes" de maintenant. Oups, double emploi avec réponse précédente.

Bonjour, Il faut commencer par calculer la masse molaire de la saccharose (c'est à dire la masse d'une mole se saccharose) Une mole de molécules de saccharose C12H22O11 contient 12 moles de C (masse molaire de C= 12 g/mol) , 22 moles de H (masse molaire de H = 1g/mol) et 11 mole de O (masse molaire de O = 16 g/mol) --> masse molaire de C12H22O11 = 12 * 12 + 22 * 1 + .... = ... g/mol Connaissant la masse molaire (donc de 1 mole) de saccharose, tu pourras calculer la masse de 0,12 mol de saccharose et celle de 22 mmol de saccharose ... et conclure.

Bonjour, On montre que les points A , G' , B , G et K sont sur une droite graduée telle que : A(0) ; G'(4) ; B(6) ; K(8) ; G(12) Comme les points A, K et K sont alignés, on a angle(BAM) = angle(KAM) on a donc les 2 relations de cos( ) : cos(BAM)=(AB^2+AM^2-MB^2)/(2*AB*AM) et cos(KAM)=cos(BAM) = (AK^2+AM^2-MK^2)/(2*AK*AM) --> (AB^2+AM^2-MB^2)/(2*AB*AM) = (AK^2+AM^2-MK^2)/(2*AK*AM) (AB^2+AM^2-MB^2)/AB = (AK^2+AM^2-MK^2)/AK (36+AM^2-MB^2)/6 = (64+AM^2-MK^2)/8 (36+AM^2-MB^2)/3 = (64+AM^2-MK^2)/4 4*(36+AM^2-MB^2) = 3*(64+AM^2-MK^2) 144 + 4AM² - 4MB² = 192 + 3AM² - 3MK² AM² - 4MB² - 48 = -3MK² et comme AM = 2MB, on a AM² - 4MB² = 0 ---> 3MK² = 48 MK² = 16 MK = 4 Double emploi ... 🙂

Pas de soucis pzorba75 Les programmes sont différents partout, à tort ou à raison ... Je ne pouvais cependant pas laisser passer des remarques fausses sur ma manière de mener les calculs, ou de les rédiger et prendre le risque que les non avertis prennent ces remarques pour argent comptant. J'ai quand même pris la peine, dans le message de "dimanche à 08:36", de donner une rédaction qui devait être comprise en France. Cela aurait du s'arrêter là sans les remarques non fondées de Chaka.

Pour clore le sujet, voila une copie faite sur le net : Encore une mauvaise rédaction ? 😎

Ce n'est pas mal rédigé, ma première réponse utilise des différentielles ... que tu ne comprends visiblement pas. Cette méthode est utilisée en supérieur et n'a rien de faux, ni de mal rédigé. Comme cette méthode semble ne pas (ou plus ?) enseignée en France, du moins à ce niveau d'étude, j'ai recommencé avec la méthode qui elle devrait être connue ... mais qui, ne t'en déplaise, n'apporte rien de plus ou de différent que celle que j'avais employée en premier.

Et bien je confirme ma réponse. Tu ne sais pas de quoi tu parles. Le "Poser t^(n-1) = u --> (n-1).t^(n-2) dt = du et poser t * exp((-t^2)/25) dt = dv ---> v = -(25/2) *exp((-t^2)/25) [...] u = t^(n-1) et v' = t * exp((-t^2)/25)". de mon message est (ET je l'ai expliqué dans un message plus loin) équivalent au message de pzorba75 quand il écrit : u = t^(2k-1) et v' = t * exp((-t^2)/25) La seule différence est qu'il remplace n par 2k dès le début et que moi je ne fais qu'au final ... ce qui ne change évidemment rien. Et dans ce que j'ai fait (une IPP avec la méthode habituelle, (donc en utilisant (uv)' = uv' + u'v)), je dis et répète que je n'ai pas fait de changement de variable, la variable d'intégration est t au début et reste t tout au long du développement. Le fait que cela te dépasse est une chose, que tu continues à raconter des sottises sur ma réponse en est une autre.

Tu racontes n'importe quoi. Pzorba a écrit dans son premier message: Pour l'IPP et en sortir, il faut considérer u(t)=t^(2K-1) et v'(t)=t*e^{-t^2/25}, Et j'ai fait exactement ce qu'il a lui même préconisé. Et ce n'est pas un changement de variable, la variable dans l'équation différentielle est t au début ... et reste t dans tout ce qui suit. C'eut été un changement de variable si en partant avec t comme variable d'intégration, on avait retrouvé plus loin une autre variable d'intégration... ce n'est ABSOLUMENT PAS le cas. La variable d'intégration est t au début et reste t tout au long du calcul.

Bonjour, Je ne comprends rien à tes calculs ... J'aurais fait ceci (pas sûr que cela soit exactement ce qui est attendu) : Bordeau : Energie lumineuse annuelle : 1600 kW.h/m² (sur document A) Avec 2050 h annuel d'ensoleillement --> P' = 1600000/2050 = 780 W/m² d'ensoleillement moyen (pendant les durées d'ensoleillement) Puissance moyenne de 1 m² de panneau (pendant les durées d'ensoleillement): (document B) courbe 800 W/m² (la plus proche des 780 W/m² estimés) --> 6,5 * 32 = 208 W (environ 200 W) Avec 10 * 1,46 = 14,6 m² de panneau --> P = 200*14,6 = 2920 W (puissance moyenne fournie par les panneaux pendant les durées d'ensoleillement) Ceci pendant 2050 h par an --> Energie électrique annuelle disponible : E = 2,920 * 2050 = 5986 kWh (environ 6000 kWh) Energie électrique nécessaire pour la maison (Document C): En = 25 * 120 = 3000 kWh Et donc l'installation de 10 panneaux photovoltaïques couvre les besoins de l'habitation du document C. ... Enfin, à condition que les panneaux soient bien orientés plein sud, avec la bonne inclinaison, sans rien pour "ombrer" et ... Et ce n'est pas non plus parce que la production annuelle des panneaux est suffisante pour que ce soit le cas à toutes périodes de l'année. Pourrait être bon sur l'énergie annuelle, mais avec un gros surplus (inutile) en été et un manque en hiver (on ne peut pas mettre le surplus produit en été dans une "boîte" pour l'utiliser l'hiver quand les panneaux risquent de "coincer").

@ manynhozoobinks Bonjour, Si tu ne comprends pas mes 2 lignes (qui utilisent la notion de différentielle, peut-être pas déjà enseignée à ton niveau) : Poser t^(n-1) = u --> (n-1).t^(n-2) dt = du et poser t * exp((-t^2)/25) dt = dv ---> v = -(25/2) *exp((-t^2)/25) Elles sont équivalentes à : Poser : u = t^(n-1) et v' = t * exp((-t^2)/25) On applique ensuite la technique de l'IPP

Je n'ai pas fait de changement de variables.

Bonjour, J'essaie en Latex ... qui, c'est vrai, n'est pas très facile à utiliser sur le site. \(\int t^n.e^{\frac{-t^2}{25}} dt\) Poser t^(n-1) = u --> (n-1).t^(n-2) dt = du et poser t * exp((-t^2)/25) dt = dv ---> v = -(25/2) *exp((-t^2)/25) \(\int t^n e^{\frac{-t^2}{25}} dt = - t^{n-1} * \frac{25}{2} *e^{\frac{-t^2}{25}}+ \frac{25}{2}.(n-1) . \int t^{n-2} * e^{\frac{-t^2}{25}} dt\) \(\int_0^\infty t^n e^{\frac{-t^2}{25}} dt =[ - t^{n-1} * \frac{25}{2} *e^{\frac{-t^2}{25}}]_0^{\infty}+ \frac{25}{2}.(n-1) . \int_0^\infty t^{n-2} * e^{\frac{-t^2}{25}} dt\) \(\int_0^\infty t^n e^{\frac{-t^2}{25}} dt = 0 + \frac{25}{2}.(n-1) . \int_0^\infty t^{n-2} * e^{\frac{-t^2}{25}} dt\) \(2 * \int_0^{\infty} t^n e^{\frac{-t^2}{25}} dt = 25.(n-1) . \int_0^{\infty} t^{n-2} * e^{\frac{-t^2}{25}} dt \) et en posant n = 2k --> \(2 * H_{2k} = 25.(2k-1) * H_{2k-2}\) \(H_{2k} = \frac{25}{2}.(2k-1) * H_{2k-2}\)

Mais cela fonctionne. C'est ton raisonnement qui est foireux. Tu confonds 2 choses: On a F(x) = ln|x| est une primitive de f(x) = 1/x (pour tout x réel différent de -6) et on a bien F'(x) = f(x) (si x est différent de 0) ... donc aussi pour x = -6 Avec f(x) = 1/x on a f(-6) = 1/(-6) et F(-6) = ln|-6| = ln(6) Mais quand tu as remplacé la variable (x) par une valeur numérique ... par exemple avec x = -6, f(-6) et F(-6) sont des valeurs numériques constantes, dériver F(-6) pour retrouver f(-6) ne peut pas se faire, la dérivée d'une constante est forcément nulle. Ne pas confondre : F'(-6) et (F(-6))' F'(-6) est la valeur NUMERIQUE que prend F'(x) lorsque x = -6 alors que (F(-6))' est la dérivée de F(-6) qui est une constante (et donc (F(-6))' = 0) **************** Ceci est vrai pour n'importe quelle fonction. Par exemple : f(x) = x ---> F(x) = x²/2 (pour tout x de R) et on vérifie facilement que F'(x) = f(x) ... Mais dès qu'on remplace x par une valeur numérique, par exemple x = 1, f(1) et F(1) ne sont plus des fonctions mais bien des valeurs numériques constantes. f(1) = 1 F(1) = 1²/2 = 1/2 Et si on calcule la dérivée de F(1) = 1/2, on trouve 0 qui n'est pas f(1) ------- Donc : "" ln(6) n'est pas une primitive de 1/(-6)"" Par contre ,si on choisit F(x) = ln|x| comme primitive de f(x) = 1/x , alors on a F(6) = ln(6) est la valeur de la primitive choisie de f(x) pour x = -6 F(6) = ln(6) n'est pas une primitive ... c'est la valeur numérique que prend la primitive considérée en x = -6 Tu vois la nuance ?

Bonjour, " ln(6) n'est pas une primitive de 1/(-6)" Cà c'est une évidence. ln(6) est une constante et donc sa dérivée est nulle. Par contre, on a bien F(x) = ln|x| est une primitive de f(x) = 1/x (pour x différent de 0) démo: Avec f(x) = 1/x pour tout x différent de 0: a) si x < 0, alors |x| = -x F(x) = ln|x| = ln(-x) F'(x) = -1/(-x) = 1/x On a donc bien F'(x) = f(x) pour x < 0 (1) b) si x > 0, alors |x| = x F(x) = ln|x| = ln(x) F'(x) = 1/x On a donc bien F'(x) = f(x) pour x > 0 (2) (1) et (2) ---> F(x) = ln|x| est une primitive de f(x) = 1/x (pour x différent de 0) ************* Attention que si on veut toutes les primitives de f(x) = 1/x pour x réel différent de 0, ajouter une simple constante à ln|x| n'est pas suffisant En effet, le domaine de définition de f(x) n'est pas connexe (pas en un seul "morceau") puisque f(x) n'existe pas en x = 0 Si on veut toutes les primitives F(x) de f(x) = 1/x, on doit écrire : F(x) = ln|x| + k1 pour x > 0 F(x) = ln|x| + k2 pour x < 0 ou si on veut : F(x) = ln(x) + k1 pour x > 0 F(x) = ln(-x) + k2 pour x < 0 k1 et k2 étant des constantes réelles quelconques. OK ?

Bonjour, 4 - 2°) Le triangle AHC est isocèle rectangle. (dessin de JulesX) On a AC² = AH² + CH² (Pythagore) et on a AH = HC (car le triangle est isocèle (angle en A et en C égaux) 1,5² = 2 * CH² CH² = 1,125 --> Aire(AHC) = 1/2 * AH * CH = 1/2 * CH² = (1/2) * 1,125 = 0,5625 (m²) Dans le triangle BHC rectangle en H : CH = HB * tan(30°) HB = RacineCarrée(1,125)/tan(30°) Aire(CHB) = 1/2 * HB * CH = 1/2 * RacineCarrée(1,125)/tan(30°) * RacineCarrée(1,125) Aire(CHB) = 1/2 * 1,125/tan(30°) = 0,5625/tan(30°) = 0,5625 * RacineCarrée(3) (0,974 m² arrondi) Aire(ABC) = Aire(AHC) + Aire(CHB) = 0,5625 + 0,974 = 1,54 m² (arrondi) ********** 5) tan(30°) = 0,577... (0,58 arrondi) La pente est de 58 % 7,5 = X * cos(30°) X = 8,66 cm Y = 3,5 - 0,0866 + 0,40 * tan(30°) = 3,64 m (Si on arrondit tan(30°) à 0,58 ... alors on trouve 3,65 m) ********** 6) Le triangle CFB est isocèle car ... --> FB = FC = 5 (m) Dans le triangle FHA (dessin de julesX) : FH = AF * sin(HAF) 10 = AF*sin(30°) AF = 20 (m) AB = AF - FB AB = 20 - 5 = 15 m --- Le triangle BFC est isocèle car ... --> CF = FB = 5 AlKashi dans le triangle BFC : BC² = FB² + FC² - 2*FB*FC*cos(BFC) BC² = 5² + 5² - 2*5*5*cos(120°) BC² = 50 + 25 = 75 BC = 8,66 m (arrondi) Pour trouver BC on peut utiliser d'autres méthodes (immédiat par règle des sinus (si connue) ou via des propriétés des triangles isocèles ou ...) ----- A toi pour CD et DE, c'est le même principe qui les calculs faits ci-dessus pour AB et BC. ************** A comprendre et savoir refaire sans aide ... évidemment. Si cela coince encore, repose des questions ... mais après avoir sérieusement cherché par toi-même.

Bonjour, Juste pour un peu remuer la vase ... Penses-tu que les 10000 moustiques battent des ailes à la même fréquence et de plus en phase ? Personnellement je n'aime pas ce genre de question (celle avec les 10000 moustiques) dont la réponse attendue est tout à fait à coté de ce qui se passerait en pratique.

Suite et fin Q14 NPN ----- Q15 7,5 mm ----- Q16 Montage Suiveur Vs1 = Vce ----- Q17 I1 = Ic (car le courant I+ dans l'entrée de l'ampli ALI1 est nul (si l'ampli est considéré comme parfait) ----- Q18 Ic = (24 - 0,3)/R1 0,21.10^-3 (23,7)/R1 3.10^-3 8,86.10^-6 1/R1 1,266.10^-4 7900 R1 112667 La résistance choisie sera la 10 kohm ----- Q19 Vs1 diminue. ----- Q21 V2- = Ualim * R6/(R5 + R6) = 24 * 0,4 = 9,73 V ----- Q22 Millman : V2+ = (Vs1/R3 + Vs2/R4)/(1/R3 + 1/R4) V2+ = (Vs1/1000 + Vs2/2200)/(1/1000 + 1/2200) V2+ = (0,001.Vs1 + 4,545.10^-4.Vs2)/0,00145 V2+ = 0,69.Vs1 + 0,31.Vs2 ----- Q23 SB = 3,2 V SH = 14 V ----- Q24 Seuil de basculement pour V2+ = V2- donc pour : 0,69.Vs1 + 0,31.Vs2 = 9,73 0,69.Vs1 = 9,73 - 0,31.Vs2 Vs1 = 14,1 - 0,45.Vs2 Si ALI2 est parfait et saturé vers le haut, alors VS2 = 24 V ?, on a alors V1 = 3,3 V Si ALI2 est parfait et saturé vers le bas, alors VS2 = 0 V ?, on a alors V1 = 14,1 V ... ce qui vérifie,aux arrondis près, les seuils trouvés en Q23 ----- Q25 Vs2(t) en rouge sur le dessin.

Bonjour, Partie B Q8 et Q9 ----- Q10 et Q11 Sur une période de 9 ms , +24V pendant 6 ms et -24V pendant 3 ms rapport cyclique = 6/9 = 2/3 tension moyenne : (24 * 6 - 24 * 3)/9 = + 8 volts --> marche avant. ----- Q12 0 rapport cyclique < 1/2 : marche arrière ----- Q13 Variation de la vitesse et sens de marche.

Je ne pense pas que le calcul pour Q5 doive se faire à 17 tr/min Il doit, pour moi se faire dans les conditions imposées dans les questions précédentes (soit avec le couple de 4 Nm ... et donc 19,5 tr/min tiré du diagramme) Pour moi, cela se confirme dans la question 6, où on demande de vérifier la puissance dans les conditions des question sprécédentes ... J'ai fait ce calcul avec 4 Nm , 19,5 tr/min et rendement 0,6 et on arrive bien à la puissance suggérée par l'énoncé.

Rebonjour, En complément à ma réponse précédente. Si tu continues à employer des unités farfelues comme le tr.min ou le m.s, tu vas te faire "boxer" par ton prof. Le tr.min n'est en cas une unité de vitesse de rotation, la notation correcte est soit : tr/min, soit \(tr.min^{-1}\) tout comme le m.s n'est en aucun cas une unité de vitesse, la notation correcte est soit : m/s soit \(m.s^{-1}\) Et ceci n'est pas une remarque anodine.