Black Jack

Bonjour; 1) Les règles de sécurité imposent que la fusée explose à une altitude supérieure ou égale à 40 mètres --> f(x) 40 -0,05x² + 4x + 5 40 -0,05x² + 4x - 35 0 2) Développer : (-0.05x+0.5)(x-70). (-0.05x+0.5)(x-70). = -0,05x² + 3,5x + 0,5x - 35 (-0.05x+0.5)(x-70). = -0,05x² + 4x - 35 Et donc -0,05x² + 4x - 35 = (-0.05x+0.5)(x-70) 3 et 4) Faire le tableau de signes de (-0.05x+0.5)(x-70) pour x dans [0 ; 80] et on doit pouvoir en déduire que (-0.05x+0.5)(x-70) 0 pour x compris dans [10 ; 70] ... Recopier sans comprendre est inutile.

Bonjour, Aide sans paroles ...

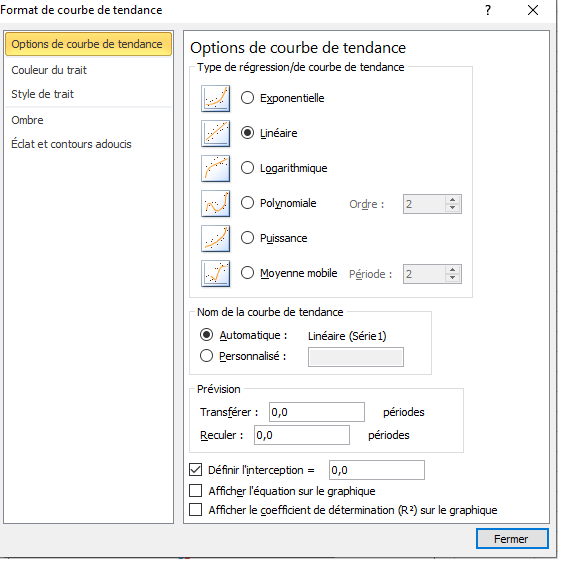
C'est disponible aussi sur Excel On trace le graphique en nuage de points. On sélectionne le graphique et on met le curseur sur un point du graphique On fait un clic droit On sélectionne : ajouter une courbe de tendance. On choisit "linéaire" Et (facultatif) on peut choisir un point où la courbe doit passer en cochant "définir l'intersection" ... où on peut imposer les coordonnées du point

Bonjour, Il faut faire un minimum d'effort pour avancer par toi même. Se contenter de recopier est inutile. Essaie de comprendre tout ce qui suit ... et tu dois être ensuite capable de tout refaire seul(e) sans aide. Question1.1.1 C'est immédiat ... si on comprend de quoi on parle. C'est écrit en toute lettre dans les données : Bouilloire de voyage : Puissance : 150 W Question 1.1.2 L'information utile nécessaire (mas pas suffisante) est : "Lorsque l'on dépense une énergie .... en moyenne de 14,4 g de CO2" (donnée malheureusement loin de la vérité, actuellement en France la moyenne est d'environ 52 g de CO2/kWh, mais a ne pas prendre en considération dans l'exercice présent) Question 1.1.3 Pour chauffer 0,6 litre d'eau (liquide) de la température ambiante (environ 20°C) à 80°C, il faut élever la température de l'eau de 80-30 = 60°C La chaleur massique de l'eau est de 4180 J/(kg.°c) et la masse volumique de l'eau est 1000 kg/m³ (soit 1kg/L) L'énergie nécessaire est donc E = m * C * (Delta theta) Avec m la masse d'eau en kg, C la chaleur massique de l'eau en J/kg (4180 J/kg) , Delta theta est la variation de température (en °C ou en K) Et m = V * Rho Avec V en m³ le volume de l'eau, Rho la masse volumique de l'eau en kg/m³ (1000 kg/m³) Donc E = V * Rho * C * (Delta theta) E = 0,6.10^-3 * 1000 * 4180 * 60 = 150480 J Ceci sans compter les pertes de chaleur dans l'air ambiant et la quantité de chaleur nécessaire à élever la température du récipient (ici la bouilloire) ... ce qui fait que la valeur de E calculée est beaucoup trop petite par rapport à ce qui arrivera vraiment. Question 1.1.4 Il faut mesurer la consommation en énergie électrique pendant la mise en température. Pour le faire, si on se fie à la puissance (150 W) indiquée pour la bouilloire, on pourra mesurer le temps (au chronomètre) que met l'eau pour passer de la température ambiante (qu'on mesurera avec thermomètre et notera la valeur) jusque 80°C (qui sera aussi mesuré avec un thermomètre) On calculera l'énergie E = P * t (avec E en Joules, P en Watt et t en secondes) Il faudra ensuite se servir des informations de la question 1.1.2 pour déterminer la masse de CO2 émise.

Bonjour, Q(k) = (k+1) * P(k) - k Q(k) = (k+1) * k/(k+1) - k Q(k) = 0 Donc les racines de Q(x) sont toutes les valeurs de k entier dans [0 ; n], soit donc (n+1) racines. Q(x) = x.(x-1).(x-2)*(x-3) * ... * (x-n) Q(n+1) = (n+1)*n*(n-1)*...*1 = (n+1)! Q(n+1) = (n+2) * P(n+1) - (n+1) (n+1)! = (n+2) * P(n+1) - (n+1) P(n+1) = [(n+1)! + (n+1)]/(n + 2) Aucun calculs vérifiés.

Bonjour, 4b) Les 4 points sont coplanaires. 5) Réfléchis ...

Bonjour, Bernoulli et pas Bernouilli. La relation dans ton dernier lien est fausse ... le "g" est en trop. En physique, quand on doute d'une "formule", il faut vérifier les dimensions. Si l'équation n'est pas homogène, elle est forcément fausse. Si l'équation est homogène ... elle est peut-être correcte. [P1] = M.L^-1.T^-2 [Rho.g.z] = M.L^-3 * L.T^-2 * L = M.L^-1.T^-2 [1/2.Rho.v²] = M.L^-3 * L².T^-2 = M.L-1.T^-2 Les 3 termes ci dessus ont les mêmes dimensions (M.L-1.T^-2) (pas de soucis quand on les ajoute) Par contre [1/2.Rho.g.v²] = M.L^-3 * L.T^-2 *L².T^-2 = M.T^-4 On n'ajoute pas des pommes et des poires ... On ne peut pas pareillement ajouter 1/2.Rho.g.v² avec P1 (ou avec Rho.g.z) ... puisque ces termes n'ont pas les mêmes dimensions.

Bonjour, J'aurais fait ceci ... Mais je ne suis pas hydraulicien. 🙂 La pompe prend l'eau à la pression Po = 10^5 Pa et la rejette à la pression P1 = 5,4.10^5 Pa --> Delta P = P1 - P0 = 4,4.10^5 Pa Section tuyau de sortie de la pompe : S = Pi * 0,12²/4 = 0,0113 m² Débit de sortie de la pompe : Qv = = S * vitesse = 0,0113 * 5 = 0,0565 m³/s Puissance de la pompe : Puissance = Qv * Delta P = 0,0565 * 4,4.10^5 = 24881 W Le but étant en général de calculer la puissance de la pompe, c'est fini. Dans l'exercice, on passe par Berlin pour aller de Paris à Versailles, on calcule l'énergie fournie par la pompe pour remonter un volume d'eau égal au volume du tuyau de sortie... Et puis, je présume qu'on devra calculer le temps de transfert de l'eau dans le tuyau de sortie (qu'on calculera de 8 s) ... et on divisera l'énergie par cette durée pour trouver la puissance utile de la pompe. '''''''' calculer l'énergie sur ces 8 s, n'est en général pas utile... on peut le faire pour vérifier : Durée de montée de l'eau dans la sortie : t = L/vit = 40/5 = 8 s Energie fournie par la pompe sur ces 8 s : E = P * t = 24881 * 8 = 199051 J (1,991.10^5 J) Un peu différent de ton calcul (que tu devrais vérifier) '''''''''''' C'est ma vision des choses, qui n'est peut-être pas celle du prof.

Bonjour, 1) P(1) = (1 - 3*0,2)/9 = 0,4/9 2) OK mais incomplet, on demande de calculer les probabilités ... donc d'en donner des valeurs numériques. Exemple : P(B) = 6 * 0,4/9 + 3 * 0,2 = 2,4/9 + 0,6 = 0,8/3 + 1,8/3 = 26/30 = 13/15 Pareil pour les autres probas.

Bonjour, u(n) = (1 + 0,5^n)/n u(n+1) = (1 + 0,5^(n+1))/(n+1) u(n+1) - u(n) = (1 + 0,5^(n+1))/(n+1) - (1 + 0,5^n)/n u(n+1) - u(n) = [n.(1 + 0,5^(n+1)) - (n+1).(1 + 0,5^n)]/[n.(n+1)] u(n+1) - u(n) = (n + n*0,5^(n+1) - n - 1 - n.0,5^n - 0,5^n)/[n.(n+1)] u(n+1) - u(n) = (n*0,5*0,5^n - 1 - n.0,5^n - 0,5^n)/[n.(n+1)] u(n+1) - u(n) = (n*0,5^n * (0,5-1 ) - 1 - 0,5^n)/[n.(n+1)] u(n+1) - u(n) = -(1 + n*0,5*0,5^n + 0,5^n)/[n.(n+1)] u(n+1) - u(n) = -(1 + 0,5^n (1 + 0,5^n))/[n.(n+1)] Et donc u(n+1) - u(n) < 0 et ...

Bonjour, Tu as fais une erreur dans l'expression de Vn. La bonne expression est v(n) = (1/2)^n C'est donc normal que tu n'arrives pas à trouver le u(n) donné dans l'énoncé. '''''''''''''''' 2) Avec v(n) = (1/2)^n (1/2)^n = n.u(n) - 1 u(n) = (1 + (1/2)^n)/n u(n) = (1 + 0,5^n)/n ''''''''''''''''''''' Tu dois donc commencer par corriger ce que tu as fait pour trouver v(n).

Bonjour, Il y a, ici, incontestablement un soucis. Le dessin accompagnant l'exercice comporte des symboles indiquant habituellement que les sections sont circulaires (on a repéré des diamètres sur le dessin par des D...) Mais, si c'est le cas, alors la vitesse de sortie calculée n'est pas de 5 m/s. Donc, il y a une incohérence quelque part. Je soupçonne fort que, comme c'est souvent le cas, un prof crée des exercices... Et un étudiant, les résout et "publie" un corrigé de ces exercices. Ce "corrigé" n'émane pas du prof qui ne le lit pas et les fautes de l'étudiant persistent dans ce corrigé. Il y a donc une bonne probabilité que ce soit le cas ici. L'exercice du prof concerne des sections circulaires ... l'étudiant qui les a résolus s'est trompé et les a considérées comme rectangulaires et s'est donc planté dans la valeur de la vitesse de sortie...

Bonjour, Voila (sur le net), un dessin qui va dans le sens que j'ai écrit pour le repérage des tuyaux cylindriques. Si ce sont des tuyaux cylindriques avec des diamètres repérés par leur diamètre extérieur et épaisseur. Le diamètre intérieur D1 = 42,4 - 2* 2,9 = 36,6 Le diamètre intérieur D2 = 21,3 - 2* 2,3 = 16,7 S1/S2 = (36,6/16,7)² = 4,8 Et on aura v2 = 2*4.8 = 9,6 m/s (arrondi) ********** Il reste possible que d'autres conventions de repérages des tuyaux existent. Par exemple que le 1er nombre représente le diamètre intérieur, mais alors on trouverait V2 = 2 * (42,4/21,3)² = 7,9 m/s (arrondi) Pas vraiment proche quel que soit le cas des 5 m/s attendu. *********** Autre possibilité : La réponse préconisée de 5 m/s est fausse.

Bonjour, PA - PB = 10 cm d'eau, soit 1000 Pa Bernoulli vA²/2 + g.zA + PA/Rho = vB²/2 + g.zB + PB/Rho zA = zB (même altitude) --> vA²/2 + PA/Rho = vB²/2 + PB/Rho VA²/2 + (PA-PB)/Rho = VB²/2 0²/2 + 1000/1000 = v²/2 v² = 2 v = sqrt(2) = 1,4 m/s (arrondi)