julesx

Bonjour et bienvenue sur le site, 1) Oui pour la limite en -infini. Pour celle en +infini, c'est simple, x*ex tend vers +infini, donc -x*ex tend vers -infini et idem pour f(x). OK? 2) Les valeurs approchées de ton équation de la tangente sont correctes, mais, à mon avis, il vaut mieux garder les valeurs exactes en fonction, en particulier, de e. 3) Avec la bonne limite en +infini, tu ne devrais plus avoir de problème.

Bonjour, Comme l'a fait PAVE, j'appelle N le nombre choisi. Calcul P1 : A=N-5 B=N+3 Résultat=A*B=((N-5)*(N+3) Je te laisse vérifier que le résultat développé est N²-2*N-15 Calcul P2 R=(N-1) S=(N-1)*(N-1) Résultat=S-16 Je te laisse vérifier que le résultat développé est aussi N²-2*N-15 On obtient bien le même résultat littéral.

Bonjour, Je ne comprends pas ce que tu entends par "on a les mêmes primitives pour un , 1/u2 et 1/un ". u est une fonction quelconque de la variable et u' la dérivée correspondante.

Bonjour, Éventuellement, si tu obtiens une correction, fais nous part de la réponse à la question sur le rendement.

Une possibilité éventuelle, c'est que le tableau de données est un "générique" et que la courbe correspond à un relevé effectué sur une éolienne de la gamme. Mais sans précisions supplémentaires sur l'origine de ces éléments, il est impossible de se prononcer.

Bonjour, Le problème, il me semble, c'est que le tableau de données techniques n'est pas tout à fait compatible avec la courbe en regard. Si on se fie à cette dernière, les 40 kW correspondent à un vent de l'ordre de 15 m/s, ce qui conduit à un rendement de 0,3627, soit environ 36%...

Allez, je rajoute aussi mon grain de sel. OK pour des demandes ne comportant QUE des pièces jointes. Par contre, je vois deux inconvénients à les interdire totalement : * Les figures sont quelque fois difficiles à reproduire à la main. * Dès qu'elles sont un peu complexes, les formules mathématiques deviennent difficiles à lire, même si le demandeur respecte au mieux l'utilisation des parenthèses. Ne parlons évidemment pas de l'élision abusive de ces dernières. Quant à l'utilisation de Latex, même si cela fonctionnait correctement sur ce site, je ne vois pas l'élève moyen se coltiner l'apprentissage de ce langage juste pour faire plaisir à certain intervenant. Donc, des pièces jointes, oui, mais du texte au clavier pour tout ce qui n'est pas strictement nécessaire.

Bonsoir anylor, J'espère me tromper, mais j'ai bien l'impression que Louanne80600 fait partie de la cohorte "je poste à l'instant t et je ne me reconnecte plus jamais, vous n'en voyez pas l'intérêt, moi non plus, c'est juste pour le fun !!!!". J'avais vu ce post et j'attendais que Louanne80600 se reconnecte pour voir s'il y avait une recherche de réponse. Comme ce n'était pas le cas, j'ai jugé inutile de donner suite. C'est une réaction que j'ai de plus en plus souvent car j'en ai marre de ce comportement. A la rigueur, je dis que j'ai vu, mais ça s'arrête là en attendant. Je sais que certains pensent autrement, chacun voit midi à sa porte... Cela dit, @Louanne80600, si, pour une raison valable, tu n'as pas pu te reconnecter, oublie ce mouvement d'humeur...

Bonjour, 3) Ta démarche serait à la rigueur acceptable à condition de séparer la passage entre 6IG=... et IG=... car, tel quel, tu finis par écrire 6IG=IG ! Idem pour JG ! En fait, pour moi, il faut utiliser les relations de la question 2). Avec tout en vecteur : a) IG=IA+AG=-AB/6+AB+AD+AE => 6IG=5AB+6AD+6AE b) JG=JA+AG=-1/4*AD+AB+AD+AE => 4JG=4AB+3AD+4AE c) KG=KA+AG=-AB-5/9*AE+AB+AD+AE => 9KG=9AD+4AE 4)a) Comme AB n'intervient pas dans l'expression de KG et qu'on veut KG en fonction de IG et de JG, il faut essayer d'éliminer AB entre les expressions obtenues pour IG et JG. 5 et 4 ont pour ppcm 20, donc on peut essayer de faire la différence 4*6IG-5*4IG : Je le laisse faire le calcul pour voir qu'on obtient 9AD+4AE. On a donc 9KG=24IG-20JG, ce qui est bien le résultat recherché.

Et pour les petits essais, trinket, logiciel en ligne, il n'y a même pas besoin d'installer quoi que ce soit. Ne pas oublier non plus que les calculettes les plus récentes ont une application Python intégrée.

Bonjour, Entre "tutoriels python" dans ton moteur de recherche. Dans le tas, tu trouveras surement un qui te conviendra.

Si je comprends bien, je suis le seul à avoir ce problème ?

Régulièrement, depuis quelques temps, lorsque j'essaie de me connecter avec mes identifiants, j'obtiens le message d'erreur ci-dessous Bon, je clique dans "Utilisateur existant", je re-valide mes identifiants et tout rentre dans l'ordre, mais c'est quand même pénible. Pour info, je suis sous Windows 10 et j'utilise Firefox avec les identifiants pré-enregistrés. Quelqu'un a-t-il un problème similaire ?

Is(t) et ip(t) sont des valeurs instantanées fonction du temps. Il n'y a pas de calcul à faire, il faut simplement les tracer, sachant que is(t) est égal à ic(t) tracé précédemment et que ip(t)=is(t) moins sa valeur moyenne (voir N.B.), donc décalé vers le bas d'une quantité constante égale à la valeur moyenne de ic(t). N.B. : Dans un transformateur, la compensation des ampères-tours entre le primaire et le secondaire ne se fait que pour les composantes alternative car les composantes continues ne créent pas de variations de flux. Par contre, pour un un transformateur réel, la présence de la composante continue au secondaire peut entrainer une saturation plus ou moins importante du noyau, mais ce n'est pas le problème ici. En ce qui concerne Iceff, comme pour Icmoy, il s'agit de calculs d'intégrales sur une période. On ne vous a pas donné les relations ? En raisonnant en termes d'angles θ=ωt, on a Iceff²=1/(2π)*∫02πic(θ)²dθ avec ic(θ)=V√2/R*sin(θ) entre 0 et π et ic(θ)=0 entre π et 2π. Une fois l'intégrale calculée, on prend la racine carrée pour obtenir Iceff. Pour info, je trouve Iceff=V/(√2R).

OK, tiens moi au courant. P.S. : Si ce n'est pas indiscret, tu suis quelle formation ?

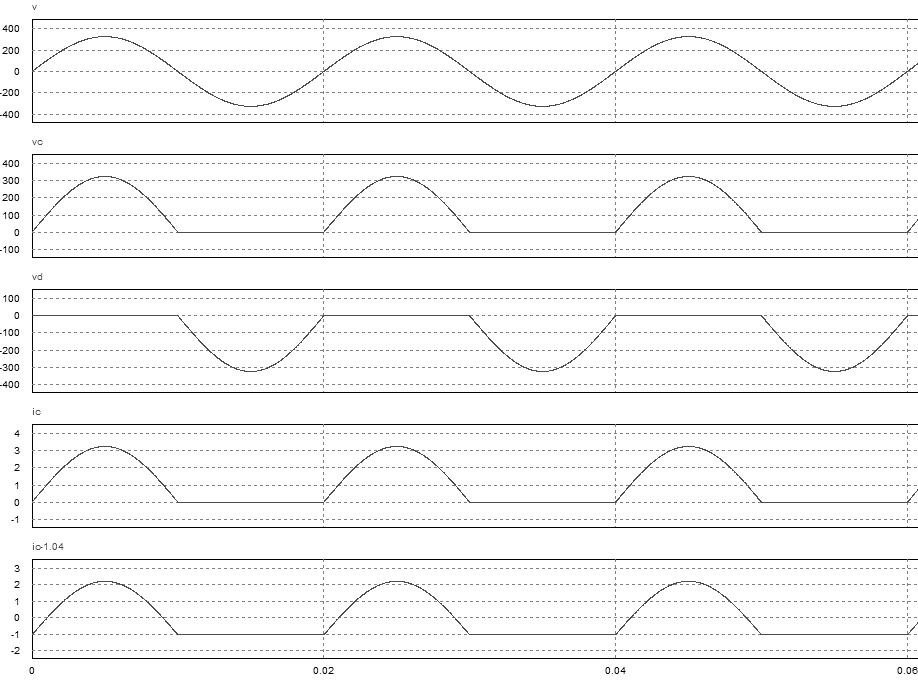
Bonjour, 1) D conduit lorsque v est positif. Donc vc est égal aux alternances positives de v et égal à 0 pendant les alternances négatives . ic=vc/R. vd=0 lorsque D conduit et vc=v lorsque D est bloquée. Pour les allures, voir pièces jointes. 2) Il faut prendre en compte l'intensité du courant et la valeur crête de la tension inverse. 3) Je ne sais pas ce que l'auteur entend par puissance moyenne. Pour moi, la seule puissance est la puissance active dissipée dans la charge, donc R*Iceff² avec Iceff valeur efficace du courant ic, à calculer. La puissance apparente S est celle au niveau de la source, soit V*Iceff. Le facteur de puissance f vaut P/S. 4) is(t) est le mème que ic(t) précédent. ip(t) est égal à is(t)-Ismoy avec Ismoy, valeur moyenne du courant is(t), à calculer. Dans les allures de courbes, ic-1.04 correspond à ip(t). 5) Au secondaire, la puissance moyenne est celle calculée précédemment. A primaire, toujours le même problème en ce qui concerne la puissance "moyenne". Le courant moyen au primaire est nul, ça, c'est sûr ! Par contre, si on raisonne en termes de puissance active, elle est égale à celle fournie à la charge, donc celle au secondaire. 6) Pour les puissances apparentes : Au secondaire Ss=V*Iseff avec Iseff calculé précédemment. Au primaire Sp=V*Ipeff avec Ipeff à calculer.

OK pour le tableau de signes et de variations de l'exercice 4, mais tu as évidemment loin d'en avoir fini avec cet exercice. Par contre, pour l'exercice 3, ça ne va pas du tout. Si tu ne retrouves pas l'expression donnée dans l'énoncé , il y a quand même pas mal de chances que l'erreur soit de de ton côté (bien que, diraient certains...). Reprenons : Déjà, au dénominateur, c'est v(x)², pas v'(x)², donc (x+11)². Cela dit, ça ne change rien à l'étude de signe puisque (x+1)² est toujours positif ou nul. Ensuite u'(x)*v(x)=(-4x+19)*(x+11)=-4x²-44x+19x+209 u(x)*v'(x)=(-2x²+19x+10)*1=-2x²+19x+10 => u'(x)*v(x)-u(x)*v'(x)=-2x²-44x+199 Ce qui conduit bien au résultat de l'énoncé. Les racines du numérateur sont -[21*√(2)+22]/2 et [21*√(2)-22]/2 dont je te laisse calculer les valeurs approchées. Il te reste à voir ce que cela te donne en termes de signes sur l'intervalle [0;10] et terminer. Par contre, là, je me déconnecte. Si un autre intervenant veut prendre le relais, qu'il n'hésite pas.

Effectivement, tu ne tiens pas compte du dénominateur, donc ta démarche n'est pas correcte car le dénominateur intervient également dans la variation de R(x). Il faut procéder comme indiqué dans l'énoncé, calculer la dérivée R'(x) de R(x), chercher son signe et en déduire les variations de R(x). Pour la dérivée, rappel, si la fonction est de la forme u(x)/v(x), sa dérivée est [u'(x)*v(x)-u(x)*v'(x)]/v(x)². ici u(x)=-2x²+19x+10 => u'(x)=-4x+19 v(x)=x+11 => v'(x)=1 Je te laisse continuer ? P.S. : Pour l'exercice 4), attention, b=-12, mais b²=(-12)²=144. Donc ton tableau de signe est à revoir. De toute façon, il ne correspondrait pas avec les courbes fournies par pzorba75.

Pour débuter l'exercice 3) : R1=10-x R2=2x+1 => 1/R=1/(10-x)+1/(2x+1)=(x+11)/[(10-x)(2x+1)]=(x+11)/(-2x²+19x+10) D'où R=(-2x²+19x+10)/(x+11)

Bonsoir et bienvenue sur le site, tu bloques où ? Exercice 3) : Il suffit d'appliquer les indications de l'énoncé pour résoudre la plupart des questions. Exercice 4): Idem, au moins pour la question 1).

Bonjour anylor, C'est une possibilité que j'avais également envisagée, mais qui pose un problème au niveau de la compatibilité avec les deux chiffres significatifs demandés pour le résultat. Le mieux aurait été de ne pas évoquer cette notion et de parler d'arrondi au milier de km.

Bonjour, Mea culpa, j'avais zappé la précision figurant dans la question 1. Cela dit, ça ne me parait pas très logique. L'élève calcule au ° près, donc ne verra pas pourquoi, au 2)b), il devrait refaire les calculs pour déterminer γ. Ce n'est pas précisé, les deux chiffres significatifs, c'est pour l'arrondi du résultat, ça m'étonnerait que beaucoup d'élèves aient le réflexe de se dire qu'avec l'arrondi initial sur les angles, le résultat avec deux chiffres significatifs n'est pas vraisemblable.

Oui et non, tu ne respectes pas les deux nombres significatifs. α=15,1° β=20,8° => γ=5,7° et P= 360 x 654/ 5,7=41 000 km (ou 4,1*104 km )avec 2 chiffres significatifs. Mais là, je me déconnecte. Bonsoir.

Oui, mais ce n'est pas tout. On te demande la circonférence de la terre et le rayon. En plus, comme on veut des résultats avec 2 chiffres significatifs, il faut en donner au moins 2 pour γ.

Donc il ne te reste plus qu'à faire les calculs.