julesx
E-Bahut-
Compteur de contenus
2 929 -
Inscription
-
Dernière visite
-
Jours gagnés
130
Type de contenu
Profils
Forums
Blogs
Galerie
Boutique
Tout ce qui a été posté par julesx
-
Mais avant de programmer quoi que ce soit, il faut déjà que palo_3 comprenne la signification des termes c et t (voire de p, e1 et e2). C'est cela qui lui permettra de répondre à la première question, donc de compléter le script. Mais visiblement, ce n'est pas son problème puisqu'elle ne répond même pas à la question de PAVE. On se demande pourquoi elle poste dans un(des) site(s) d'aide.
-
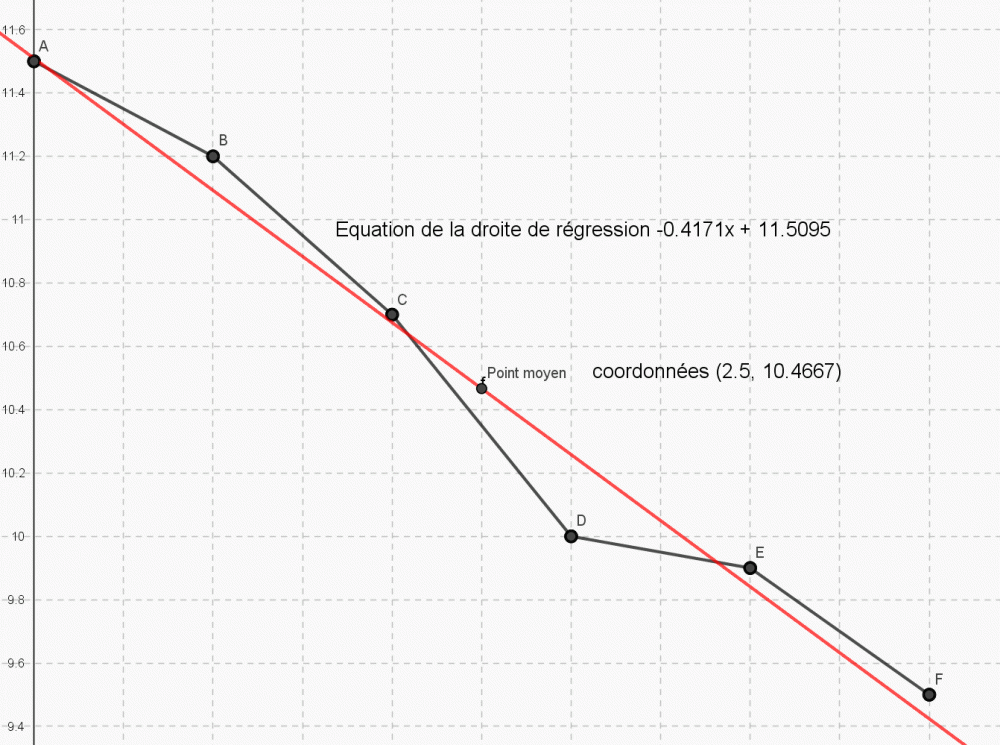
@Paul45, Juste une petite remarque. Je n'avais pas pu voir dans tes premiers messages que tu déterminais "à la main" l'équation de la droite de régression. Comme, dans ce cas, tu utilises les coordonnées du point moyen pour calculer b, la droite passe forcément par ce point. Cela dit, pour la vérification numérique, je trouve ta démarche un peu maladroite. Pour moi, il aurait mieux valu vérifier que tu trouves le bon y à partir de ax+b plutôt que de déduire a de x et de y. Bonnes fêtes de fin d'année également.
-
Bien sûr, ci-joint cadeau de Noël, merci Geogebra, Il ne reste plus, si ce n'est pas fait, qu'à retrouver l'équation de la droite de régression et à calculer les coordonnées du point moyen, puis qu'à vérifier que ces coordonnées vérifient l'équation précédente (aux arrondis éventuels près).
-
OK, bonne continuation.
-
Bonjour, Tu arrives à quelque chose ? Oublie tes difficultés et raisonne simplement à partir de phrases clés qui suivent le tracé du triangle équilatéral : Programme 1 : Avancer de 50 pas => Tracé du carré décalé vers la droite. Programme 2 : Avancer de 100 pas (donc du double) => Tracé du carré décalé vers la droite du double de la distance précédente. Programme 3 : Tourner de 60° => Tracé du carré tourné de 60°. Partant de là, tu devrais pouvoir relier chaque programme à son image.
-
Juste une rectification, il fallait lire ”pas de donnée pour V=80 km/h”.
-
Bonsoir, Revois ton graphique, il y a une erreur pour V= 60km/h, c'est 22 m pas 32 m et il n'y a pas de donnée pour V =8 km/h. Comme ton professeur ne veut pas de graphique, tu crées un tableau avec une ligne pour les Df, une ligne pour les Ec et une ligne pour le rapport Df/Ec. Si, dans cette dernière ligne tous les termes sont approximativement constants, tu en conclus qu'il y a proportionnalité.
-
Bonsoir, A priori, cf. 2)a, un est croissante est majorée, donc un converge. Dans ce cas, sa limite L vérifie un+1=un, soit L=4L(1+3L). Je te laisse terminer.
-
Dans ma réponse ce sont les valeurs extrêmes de g(x) dont je parlais, pas de celles de x. OK, c'était un peu mal formulé, en fait, je voulais me passer du tracé d'un tableau de variations, même sommaire.
-
Bonjour, Ce n’est pas un problème de contestation, simplement, au départ, Dtm parlait d’un problème avec la TI82, qui avait un peu été ignoré.
-
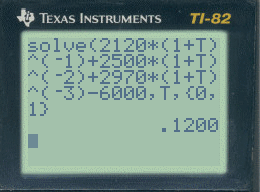
C'est bien, mais je persiste et signe, la fonction "solve" de la TI82 permet bien de résoudre les équations à condition de la configurer correctement et, bien sûr, que les équations aient au moins une solution réelle. Ici, ce n'est pas le cas, mais si on cherchait la solution de 2120(1+t)^-1+2500(1+t)^-2+2970(1+t)^-3=6000, on procèderait comme indiqué ci-dessous pour obtenir t=0,1200
-
OK pour g'(x) mais cette fonction n'est pas toujours négative ! -ex+ea=0 pour x=a, -ex+ea>0 pour x<a et -ex+ea<0 pour x>a (voir comportement de la fonction exponentielle). Le cas x=a était d'ailleurs évident, la distance entre la courbe et sa tangente étant forcément nulle au point de tangence ! Partant de là, tu vois que g(x) croît entre moins l'infini et 0 g(x) décroît entre 0 et l'infini donc que g(x) passe effectivement par un maximum pour x=a, ce maximum valant bien 0, il s'ensuit que g(x) est toujours négatif et nul. Tu en déduis que la courbe est toujours sous sa tangente. Cela dit, revois la réponse de pzorba, c'est beaucoup plus simple avec sa méthode.
-
Il y a pléthore de cours sur la toile. Pour les relations de base, voir par exemple ici : https://www.pass-education.fr/lois-des-circuits-cours-4eme-physique-chimie-college/
-
Deux petites remarques : * La calculette TI82 possède une fonction solve, accessible en pressant la touche MATH et en déroulant le menu. La procédure est décrite dans le manuel, normalement fourni avec celle calculette. Ici, évidemment, cela n'aboutirait pas puisque l'équation n'a pas de racines réelles. * Vu la forme des dénominateurs, la réduction au dénominateur commun donne sans difficulté un trinôme au numérateur, 2120(1+t)²+2500(1+t)+2970=2120*t²+6740*t+7590, qu'on peut ensuite un peu simplifier. Nul besoin donc de passer par un changement de variable et des calculs compliqués en complexe.
-

J ai besoin d aide pour un exercice de python
julesx a répondu à un(e) sujet de Adn dans Des questions ?
Bonjour Denis, Merci pour le tuyau. Cela dit, personnellement, je déroule systématiquement le forum, donc je ne rate rien, c'était plutôt un conseil à la demanderesse, tout le monde ne procède pas forcément ainsi. Ne reste plus qu'à espérer que Adn revienne... -
Bonsoir, Je ne vois pas ce que ce sujet vient faire en informatique. Reposte le en physique et en redressant l'image, ceux qui travaillent sur PC de bureau t'en sauront gré.
-

J ai besoin d aide pour un exercice de python
julesx a répondu à un(e) sujet de Adn dans Des questions ?
Bonjour Denis, Moi, ça ouvre dans "Forum", je n'ai jamais regardé cela de près, on peut changer la page d’accueil ? -

J ai besoin d aide pour un exercice de python
julesx a répondu à un(e) sujet de Adn dans Des questions ?
Bonjour, Petites questions : * Est-ce que tu veux un script complet ? * Les données sont introduites une par une ou sous forme d'une liste ? * On demande simplement l'affichage des 4 données, c'est bien ça ? * Pour moi, "odd" veut dire impair, et dans cas , la médiane est la valeur centrale, pas la demi-somme. J'ai commencé le script, mais j'attends tes réponses pour le finaliser. P.S. : Il aurait mieux valu poster dans le forum Informatique, les intervenants ne "descendent" pas toujours jusqu'à cette rubrique. -
Ok, tu as trouvé les coordonnées du point d'intersection ? Mais n'attend pas jusqu'à lundi soir minuit !!! Et si c'est encore reporté, la moindre des politesses serait de prévenir !
-
A priori, la littérature semble considérer plusieurs régimes de frottement, dont le régime laminaire, frottement proportionnel à v et le régime turbulent (ou régime de turbulence) frottement proportionnel v². Ces deux apparaissent dans ton équation.. Mais, cette équation pose problème ! En particulier, si z désigne l'altitude, il y a entre autres un problème d'homogénéité entre m(dvz/dt) et mg. Il faudrait que tu postes exactement cette équation en précisant la signification de toutes les variables. Un scan ou une photo de l'énoncé ?
-
Bonsoir, Comme c'était pour aujourd'hui, je suppose qu'on peut considérer ce fil comme résolu.
-

besoin d'aide exercice programmation en C
julesx a répondu à un(e) sujet de 100visage dans Informatique
Bonjour, Je ne sais pas si j'ai bien saisi l'énoncé, voilà comment je l'ai compris : * on considère tous les nombres n impairs entre 1 et Max * si n n'est pas un multiple de (Max+1)/4, on l'ajoute à la somme S des nombres précedents * on affiche la somme. Exemple : Pour Max=11, (Max+1)/4=3, dont les multiples sont 3, 6 et 9. On additionne 1,5,7 et 11 en omettant 3 et 9. Mais si ce n'est pas la bonne interprétation, oublie ce message. Pour info, je n'y connais rien en C, je te joins à tout hasard un code en Python, j'ai vu qu'on devrait pouvoir le traduire assez facilement en C. Le print(i) intermédiaire peut être supprimé, il n'est là que pour voir si ça se passe bien. for Max in range(3,21,2): Mult=[] m=(Max+1)%4 if m==0: a=(Max+1)//4 n=1 while n*a<Max: Mult.append(n*a) n=n+1 S=0 print("Max =",Max) for i in range(1,Max+1,2): if i not in Mult : S=S+i print(i) print("S =",S) print("---------------") -
Oui, et tu dis que les coordonnées de I vérifient cette équation, ce qui te permet de calculer la valeur de t. Tu obtiens ainsi les coordonnées du point d'intersection recherché.
-
Bonsoir, Tu as fait un schéma ? Partant de là, ce n'est plus qu'une histoire de sinus puis de cosinus.
-
OK, sinon, la suite sera pour demain (ou avec un autre intervenant).