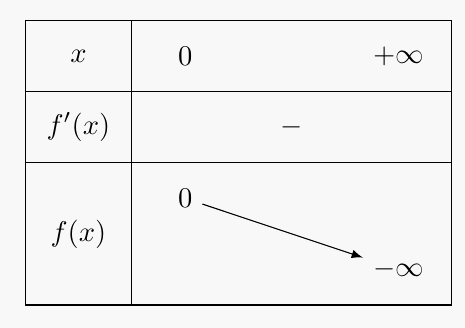Classement

Bonjour PAVE, Après bien des cogitations et l'aide de Python (pourquoi Python, parce que c'est bon, pour plagier un vieux slogan), je suis arrivé aux résultats suivants : 2*(295+354+156-133-176)=992 2*(224+93+243-168-182)=420 donc la solution serait 2*(138+73+114-85-186)=108 Mais à part ma méthode bourrin, je ne vois pas le raisonnement qui conduirait à cela. Pour info, le script Python où il suffit de remplacer les valeurs de la liste L par celles de L0, L00 ou L000. L0=[295,133,354,156,176] L00=[224,168,93,243,182] L000=[138,85,73,114,186] for i in range(0,5): for j in range(i+1,5): L=[138,85,73,114,186] L1=L[i] L2=L[j] L.remove(L1) L.remove(L2) print(i,j,L1,L2,2*(sum(L)-(L1+L2)))

La question est la suivante: « Les sciences peuvent-elles prétendre à l’objectivité dans un monde soumis aux interprétations? »

Bonjour, J'ai bien vu ta demande d'aide, mais, désolé, je suis comme toi, je bloque sur la question 3)b. J'ai bien vu une démonstration mais qui me parait curieuse : inégalité appliquée au numérateur => >=1+x inégalité appliquée au dénominateur => >=1+(n+1)/n*x on compare (1+x/n)*(1+x) à 1+(n+1)/n*x pour aboutir à x² à gauche et 0 à droite dont on déduit qu'on a bien l'égalité qu'il fallait démontrer. Mais pour moi ça revient à faire le rapport de deux inégalités... Un autre intervenant ?

Bonjour à tous, Je me permets de relancer ce sujet vu ce qui s'est passé depuis la rentrée scolaire. Récapitulatif sauf oubli de ma part : Un sujet en français sans réaction de notre part. Deux sujets en philo sans réaction non plus. Deux sujets en maths avec réaction d'un intervenant mais sans retour. Un sujet en sciences avec réaction et suivi partiel. En ce qui concerne l'absence de réaction des intervenants (ainsi que les sujets pointus comme Economie/Gestion/Compta), s'il n'y a plus personne pour répondre, autant les supprimer de ce site, ça évite que les éventuels demandeurs se posent des questions sur le sérieux de ce site.Quand au manque de suivi, déjà évoqué précédemment, il semble bien qu'il n'y ait pas de solution. J'estime qu'il faut cependant persévérer, Bonne continuation à tous.

Bonjour, La notion d'encadrement est utilisée dans différents contextes, je te conseille d'aller jeter un coup d’œil sur la toile. Ici, vu le contexte, je pense qu'il faut trouver pour chaque signe de x deux fonctions g(x) et h(x) telles que g(x)<=[f(x)-f(0)]/x<=h(x). Ici, on va d'ailleurs se trouver dans un cas particulier où une des deux fonctions est constante mais cela fait aussi partie du cas général. A titre d'exemple, je vais traiter le cas x>0. Je te laisse faire l'autre dans le même ordre d'idées. Je remplace évidemment f(0) par 1. On part de x-x³/6<=sin(x)<=x on divise par x (positif, donc ne change pas le sens des inégalités , attention au cas x<0) 1-x²/6<=sin(x)/x<=1 on retranche 1 -x²/6<=sin(x)/x-1<=0 et on divise par x -x/6<=[sin(x)/x-1]/x<=0 pour obtenir l'encadrement cherché (avec le cas particulier d'un des termes constant).

Pour info, une possibilité de tracé du tableau dont je parlais ci-dessus.

Bonjour, Non, il manque le plus important. La fonction est décroissante, mais elle pourrait parfaitement décroitre à partir d'une valeur positive, donc f(x) ne serait pas toujours négatif. Il faut chercher les limites pour x=0 et x infini. x=0 => f(x)=0 x infini => f(x) tend vers - l'infini Là , tu as montré que f(x) est toujours négatif. Le mieux dans ce type d'étude est de tracer un tableau de variation.

Non, il ne faut surtout pas réagir ainsi. Tu as oublié ce type de démarche, c'est humain, on ne peut pas tout se rappeler, surtout que vous ne l'avez peut-être que peu utilisée. Bon, là, je me déconnecte au moins jusqu'à demain après-midi. De tout façon, si nécessaire, il y a d'autres intervenants amateurs de maths. Bonsoir

Bonjour, Dans ce contexte, j'ai toujours vu qu'on étudiait le signe de la fonctions f(x)=sin(x)-x par la méthode traditionnelle.

Bonjour, Le problème dans cette inéquation est la présence de la racine carrée. En élevant au carré les deux membres, tu escamotes ce problème. Avant de faire cela, il faut voir les valeurs possibles de x. primo x+1 doit être positif ou nul donc x>=-1 secundo x<=2 => x-2<=0 donc l'inéquation est toujours vérifiée. Il faut donc combiner cela avec le fait que e trinôme est négatif pour (5-sqrt(13))/2<x<(5+sqrt(13))/2. OK ?

Bonjour anylor, Je ne sais pas si c'est une perte d'attrait, mais il est vrai que les demandeurs se font extrêmement rares. Et, quand il y a une demande, une fois sur deux, c'est hors des compétences de nos intervenants. De plus, quand c'est dans les compétences, à de rares exceptions près, nos réponses restent sans réaction des demandeurs. Amicales salutations. Julesx

Bonsoir, Bravo pour le retour, ça devient tellement rare sur ce site 😀 En ce qui concerne "empreindre", a priori, ce verbe signifie "laisser une trace" d'après quelques informations glanées sur la toile. A moins d'avoir des chaussures crottées ou de marcher pieds nus mouillés (ou sales), je ne vois pas comment on peut laisser des empreintes sur un escalier. Mais je ne suis pas spécialiste, poste éventuellement dans le forum "Français" en demandant des explications. Cela dit, c'est peut-être une simple erreur de frappe ou une correction malencontreuse dont sont friands nos logiciels de messagerie. Bon week-end et à une autre fois, peut-être.

Bonjour, Aide sans paroles ...

Comme celle-là :

Bonsoir Denis, Je pensais bien que ce n'était pas dans les cordes de notre administrateur, c'était plus un billet d'humeur qu'une vraie demande. Entre temps, j'ai consulté la liste des derniers visiteurs, on voit quels posts ont été regardés, mais ça s'arrête aux dernières 30(?) minutes donc il faudrait ne faire que ça si on voulait exercer un vrai contrôle. Cela dit, les demandes deviennent de plus en plus rares, donc il vaut mieux répondre, même si on sait qu'on aura peu de chances d'avoir un retour. Bon week-end prolongé.