julesx

Si, ton tableau correspond aussi bien à ton interprétation qu'à la mienne.

Non, a priori, c'est le nombre d'allumettes supplémentaires qu'il faut utiliser pour créer un nouvel étage. Mais cela représente effectivement aussi le nombre d’allumettes du premier étage.

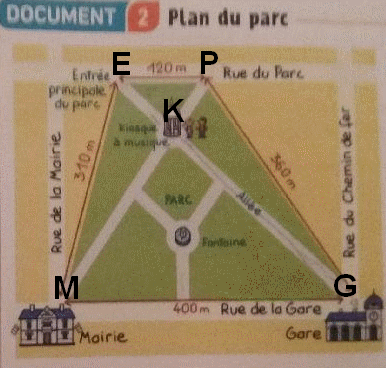
Bonjour, Avec les notations de volcano47 et le rappel de Thalès EK/KG = EP/MG qui donne KG=EK*MG/EP il suffit de lire les distances correspondantes sur le plan.

Bonjour, Tes calculs sont justes, mais ce n'est pas terminé, l'énoncé demande de déterminer la bonne réponse dans les choix proposés.

Juste une précision, quand je dis cela c'est que j'évoquais un tracé complet de chacune des courbes, évidemment pas celui des asymptotes !

C'est ça.

Lors de l'étude des limites, tu as dû trouver que pour f(x) * en plus et moins l'infini, f(x) tend vers 2 graphiquement cela se traduit par une asymptote horizontale d'équation y=2 * pour x=-5, f(x) tend vers +infini ou -l'infini ceci se traduit graphiquement par une asymptote verticale d'équation x=-5 pour g(x) * en plus et moins l'infini, g(x) tend vers -3/2 graphiquement cela se traduit par une asymptote horizontale d'équation y=-3/2 * pour x=-1/2, g(x) tend vers +infini ou -l'infini ceci se traduit graphiquement par une asymptote verticale d'équation x=-1/2 Tu peux vérifier cela à l'aide de ta calculatrice ou d'u logiciel type Geogebra. Par contre, là je me déconnecte. Si nécessaire merci à un autre intervenant de prendre le relais. Sinon, à demain, éventuellement.

Donc, tu peux passer à l'exercice 90 ? Qu'est-ce qui t'arrête dans celui-ci ?

Donc, je pars de un+1=un*(1-1/(n+1)²) un=(n+1)/(2*n) par hypothèse 1-1/(n+1)²=(n+1-1)*(n+1+1)/(n+1)²=n*(n+2)/(n+1)² => un+1=(n+1)/(2*n)*n*(n+2)/(n+1)²=(n+2)/(2*(n+1) après simplification par n et par n+1 comme n+2 peut s'écrire n+1+1, on a finalement un+1=(n+1+1)/(2*(n+1)) L'hérédité est vérifiée. OK ?

1)a 1-1/k²=(k²-1)/k² k²-1=(k-1)*(k+1) une des identités remarquables qu'il faut connaitre d'où le résultat. 1)b Initialisation n=2 1-1/2²=3/4 (2+1)/2²=3/4 Initialisation vérifiée. Hérédité Proposition vraie au rang n : un=(n+1)/(2*n) Proposition vraie au rang n+1 ? un+1=un*(1-1/(n+1)²)=... Je te laisse continuer ?

A priori, oui, qu'est-ce qui t’arrête ?

OK, donc pour l'exercice 70: 1.a) Pas de difficulté, tu réduis au même dénominateur 1-1/k². b) Procède par récurrence, tu connais, je suppose. 2) Divise numérateur et dénominateur par n et fais tendre n vers l'infini.

Bonjour, Est-tu toujours en 1ère (cf. tes posts d'octobre 2019) ? Sinon, rectifie ton profil.

En fait, pour l'utilité du 4ème satellite, voir, par exemple, https://fr.wikipedia.org/wiki/Global_Positioning_System

Bonjour, Pour moi, il s'agit d'une faute de frappe dans l'énoncé, c'est a.Trace un segment [AB] de longueur 10 cm. Sur ce segment, place les points C, D, E et F tels que AC = CD = DE = EF = FB = 2 cm. P.S. plus tard : J'ai vu qu'entre temps, tu es revenue sur ce site. J'aurais aimé savoir si tu es d'accord avec ma rectification et si, pour le reste, tu as su faire. Ceci, pour dire que le principe de ces sites d'aide, c'est aussi d'avoir un petit retour aux réponses que peuvent donner les intervenants.

Bonjour, Il faudrait commencer par dire ce qu'il y avait dans les 8 questions précédentes ! Il doit sûrement y figurer des éléments permettant de répondre à ces questions, du style de ce qui a été donné dans les différents posts de ce fil.

Bonjour, Tes graphiques sont corrects, par contre, joins les points pour obtenir un tracé de courbe. 5) Recherche sur ton graphique à quel endroit la courbe de puissance passe par un maximum et regarde le courant correspondant, noté I0 dans l'énoncé. 6) Regarde sur la courbe U=f(I) la valeur U0 de la tension correspondant à I0. 7) R=U0/I0. Pour info, chez moi, le maximum se trouve au voisinage du point (36,5 mA; 0,403 V).

Je suis bien d'accord, mais, pour moi, si, dans un script, on définit une fonction en annexe, c'est pour l'utiliser dans la partie principale. Si c'est juste pour le plaisir d'employer un def... Petite question à laquelle je n'ai pas trouvé de réponse (mais je n'ai peut-être pas assez cherché). Dans un résultat d'opération, Python affiche a priori 15 décimales. On peut évidemment demander un affichage réduit, mais si on ne connait pas au départ la valeur que va prendre le résultat, on risque de passer à côté du but recherché. Je me demandais donc s'il existait une alternative au "round".

Juste un détail. Pourquoi, dans rapport, recalculer les random() alors qu'on a défini la fonction point() qui fait le travail ? x=point()[0] y=point()[1] m'aurait paru plus logique.

Bonjour, Qu'est-ce qui t'arrête exactement ? Je suppose que tu sais te sezrvir de Geogebra au moins partiellement. Donc : * As-tu fait tracer les courbes f(x)=x² et g(x)=1/x ? * As-tu placé les points A et B ? * As-tu fait tracer les tangentes ?

De rien, bonne continuation.

Bonjour, Désolé si j'arrive trop tard, il aurait peut-être fallu que tu demandes un peu plus tôt. Exercice 1 1) Les rayons du soleil sont parallèles, donc en utilisant l'égalité des angles alternes-internes, l'angle en O vaut 5 °. 2) La circonférence vaut 553*5/360 = 39816 km. Je te laisse en déduire le rayon correspondant. 3) Calcule le pourcentage d'erreur en prenant la valeur exacte comme référence. Exercice 2 Un petit début 1) angle(AMC)=180-34-22=124 ° AC/sin(AMC)=AM/sin(34)=MC/sin(22) => AM=10/sin(124)*sin(34) MC=10/sin(124)*sin(22) Je te laisse terminer les calculs. La suite est du même ordre.

OK, donc tout va bien. Bonne continuation.

Bonjour, Ton système est évidemment correct, mais, bien sûr, pas les valeurs que tu as trouvées pour t et k. Pourrais-tu poster ta suite de calculs pour voir ton erreur (ou tes erreurs).

Bonsoir, Je ne suis pas spécialiste, loin de là. J'ai l'impression cependant qu'il manque une donnée pour résoudre le problème. D'après ce que j'ai pu lire, il y a 3 cas possibles, A//A, A//S et S//S. Parmi ces 3, si j'ai bien compris, les porteurs sains sont ceux correspondant à A//S donc, cela ne permet pas de voir la répartition entre les A//A et les S//S, or ce sont de ces derniers dont tu cherches le taux. Désolé de ne pas pouvoir t'aider davantage. Un autre intervenant, peut-être ?