PAVE

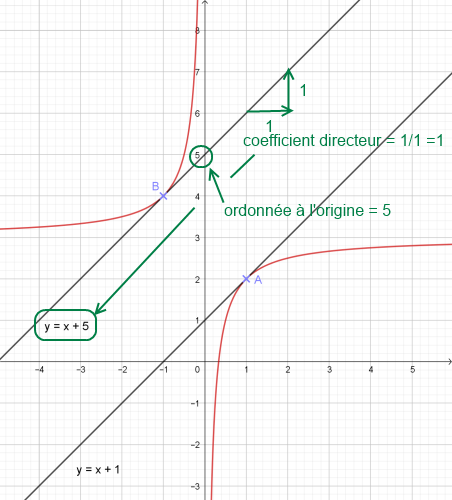
Grand silence.... 1ère méthode : par lecture graphique (à n'utiliser que si l'énoncé le demande ou pour VERIFIER)

Est-il utile que nous abordions l'exercice suivant ?

Bonjour, Fais comme moi, regarde les tutos ci-dessous.... pour revoir comment traiter ce type d'exercices ultra classiques (il y a plus de 50 ans... que je n'en ai pas fait 🤭) https://www.youtube.com/watch?v=gBU_zkds7aU (bien sûr tu peux te limiter à la 2ème méthode) https://www.youtube.com/watch?v=vOQ_cri5XhM (en complément)

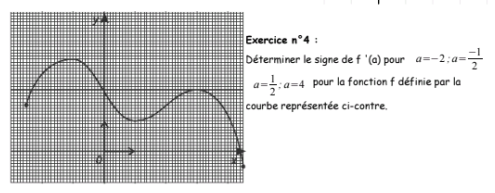
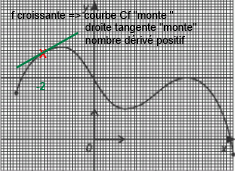
Bonsoir, A l'avenir : UN seul exercice par message. Quelques rappels de cours (à connaitre !!) f '(a) est la valeur prise quand x = a par la fonction f', fonction dérivée de f. Cette valeur f'(a) est appelé le nombre dérivé de f quand x= a et (super important) il est le coefficient directeur de la droite tangente à la courbe représentative de f Si sur un intervalle, la fonction f est CROISSANTE, sa courbe représentative Cf "monte". Alors en tout point de Cf d'abscisse a, la droite tangente "monte" et donc son coefficient directeur f'(a) est positif. Je te laisse trouver ce qu'il en est quand la fonction f est DECROISSANTE... Revenons à ton exercice : signe de f'(a) si a= -1/2 Essaye de faire la suite de l'exercice et donne nous tes réponses... on saura si tu as compris et on pourra si besoin reprendre notre aide. A toi.

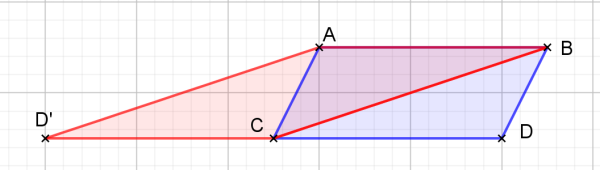
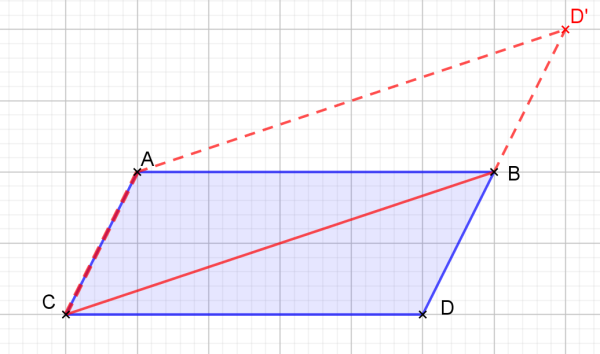
Il faut toujours appliquer à soi-même les conseils que l'on donne aux autres... Merci Denis de m'avoir rappelé que j'aurais dû : 1) bien respecter l'ordre des sommets 2) et à une heure tardive aller dormir plutôt que de faire des bêtises 🤨. Djembé55, je revendique le droit à l'erreur 🤭 😁 et voici ma deuxième tentative....

Bonsoir, Sans un énoncé COMPLET, il est un peu difficile de pouvoir t'aider.... 🥲 Respecte bien l'ordre des sommets : ABDC. A cette heure tardive tu devrais vite aller dormir....🧐

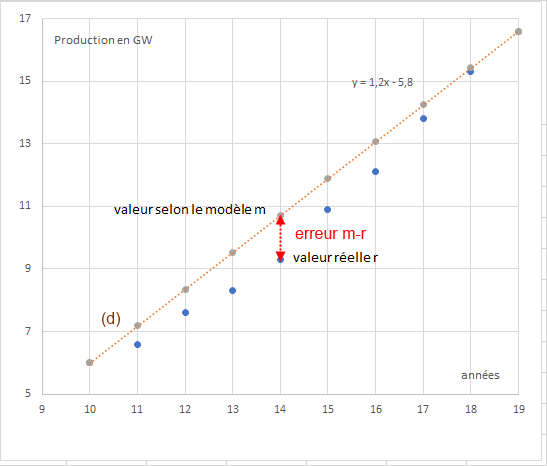
Si tu as tracé la droite (d), il est manifeste qu'elle est un mauvais modèle d'ajustement (tu connais ce mot ??) des données observées entre 2010 et 2019. Pour chaque année (sauf 2010 et 2019 bien sûr), la valeur donnée par le modèle (m) est supérieure à celle observée en réalité (r) donc chaque année, le modèle surestime la réalité. Par exemple pour l'année de rang 14 (2014 d'après l'énoncé), * la valeur estimée m est 10,7 GW si on prend pour modèle la droite (d) et... sa fonction affine associée f(x) = 1,2x-5,8. * alors qu'en fait, en réalité, la production observée r n'a été que de 9,3GW. En 2014, le modèle choisi fait commettre une erreur d'évaluation de 1,4 GW. Tu peux bien sûr faire le CUMUL des erreurs pour les 10 années connues (avec un tableur, pourquoi pas 🤭)

En attendant que Jules revienne sur le site...

La réponse "NON" catégorique et ferme de Pzorba me semble pertinente 😟. Il n'y a pas à hésiter.... on est "tous" d'accord. 😅

Bonjour, Bonne question !! Sans certitude absolue, j'opterais pour 4km à l'aller et 4 km au retour. N'y a-t-il pas dans l'énoncé des indices permettant de trancher ?

Tu peux essayer de traiter la question 3 (limites). limite de g(x) quand x tend vers -oo ? élémentaire. limite de g(x) quand x tend vers +oo ? forme indéterminée qui peut être levée en mettant ex/3 en facteur dans l'expression de g(x).

Désolé de devoir te le dire mais ma réponse est NON. Si tu ne finis pas la question 1a), il n'est pas raisonnable de vouloir traiter la question 1b) Tu peux essayer de faire la question 2. Si tu as déjà traité des questions de ce type (positions relatives de 2 courbes Cf et Cg) tu dois savoir que l'on compare f(x) et g(x) en résolvant par exemple : sur un intervalle, Cf est AU DESSUS de Cg équivaut à f(x)>g(x) ou encore à f(x) - g(x) >0 ou encore f(x) -g(x) POSITIF D'où la méthode : L'étude du signe de f(x)-g(x) selon les valeurs de x permet de déterminer la position de Cf par rapport à Cg

Oui mais as tu VU pourquoi ? Donc g'(x) = ???? Dans la continuité du 1a), tu devrais, maintenant que tu as g'(x), pouvoir trouver l'équation de la droite tangente T'0 c'est à dire la tangente à Cg la courbe représentative de la fonction g, en son point d'abscisse 0. Essaye ensuite de compléter ta réponse à 1a) en calculant : * la fonction dérivée de la fonction f : f '(x) = ??? * l'équation de la tangente à Cf au point d'abscisse 0. Pour cela : point de tangence (0;f(0)= ??) coefficient directeur de la droite tangente f '(0) = ??? équation réduite de la droite tangente à Cf au point d'abscisse 0 : ???? Quand tu auras trouvé les équations des 2 tangentes T0 et T'0, sauras tu trouver les coordonnées du point d'intersection de ces 2 droites ?

Si c'était faux (déjà dit), cela reste faux (je ne peux que le redire 😟). Pourquoi ce signe "+" ? STOP. Alexandre il faut que tu arrêtes de dire n'importe quoi. En France tout au moins, ton énoncé n'est pas conforme au programme de SECONDE.

Si la fonction g est définie par g(x)= ex/3 - 1/2*ex-3 g est une différence de 2 fonctions : g est de la forme u-v donc g' sera de la forme u'-v' [c'est du cours à connaitre] ex/3 a pour dérivée (1/3) ex/3 ex-3 a pour dérivée 1*ex-3 = ex-3 et en conséquence 1/2*ex-3 a pour dérivée 1/2*ex-3 [rappel si k est une constante, ku a pour dérivée ku'] donc g'(x) = ????

Non, c'est presque bon... mais pas bon.

Difficile de comprendre ce que tu demandes. Peut-être que le français n'est pas ta langue maternelle ? ceci expliquerait tes difficultés. N'hésite pas à nous le dire car alors, on essaiera d'adapter nos explications. Je te donne le début du calcul de la fonction dérivée de g (on dit simplement la dérivée de g...) Si la fonction g est définie par g(x)= ex/3 - 1/2*ex-3 g est une différence de 2 fonctions : g est de la forme u-v donc g' sera de la forme u'-v' [c'est du cours à connaitre] On pose u(x) = ex/3 => u'(x)= ???? (relis mon 1er message : la dérivée de eu est u'eu donc eu(x) a pour dérivée u'(x)*eu(x)) Essaye de faire : si u(x) = ex/3 => u'(x)= ????

Donc niveau première.... d'accord ! Je pense que tu confonds la fonction dérivée de f [notée f ' , elle est définie par l'expression de f'(x)] et le nombre dérivé de f au point d'abscisse "a" [ noté f '(a), ce nombre n'est autre que le valeur de f '(x) quand x= a]. Prenons un exemple élémentaire : Soit la fonction f qui à tout nombre x réel fait correspondre son "cube" ; on a f(x)= x³. La fonction dérivée de f est la fonction notée f ' qui à tout nombre réel x fait correspondre l'expression f '(x) = 3x² (démontré en cours et à connaitre !!) Le nombre dérivé de f au point d'abscisse 5 (par exemple), introduit initialement en cours comme étant le coefficient directeur de la tangente à la courbe Cf représentative de f en son point d'abscisse 5 est égal à.... 75. Ce nombre n'est autre que la valeur prise par la (fonction) dérivée de f quand x= 5 et est noté f '(5)= 3*(5²) = 3*25 = 75. D'une manière générale le nombre dérivé de f pour x= a (qui est le coefficient directeur de la droite tangente à Cf au point d'abscisse x=a) est f '(a). fonction f définie par f(x) dérivée f' définie par f '(x) nombre dérivé de f en x= a est égal à f '(a) [bien se rappeler que ce NOMBRE est le coefficient directeur de la tangente à la courbe représentative de f au point d'abscisse a]

Bonjour Alexandre et bienvenue sur e-bahut. Entre "je comprends RIEN" et "je comprends TOUT", le nombre de situations intermédiaires est infini 😀. Les indications fournies à l'instant par Jules devraient logiquement t'aider à améliorer "ta" situation entre RIEN et TOUT. Deux "coups de pouce" en complément : 1) le cours dit que si f = eu alors f '= u'eu . Formule que tu connais, je pense... et qui permet d'établir facilement les expressions de f ' et de g'. 2) ta calculatrice de compétition 🤗, peut en 1 min te tracer les 2 courbes à étudier.... de quoi découvrir de visu les principales réponses que l'on te demande de démontrer (... bien sûr). Aide toi, le ciel Jules t'aidera (et nous aussi 😇) A toi de dire...

Bonsoir, Pour compléter les informations qui t'ont été déjà données par mes collègues et pour reprendre point à point et dans l'ordre les questions de l'énoncé... a) placer les trois points A, B et C dans un repère n'a pas dû te poser de problème b) mais es tu parvenue à construire le point K, centre du cercle passant par les 3 points A, B et C ? Dis nous si tu as su faire ? On peut t'expliquer cette construction... si besoin.

Bonjour Maud, Voir https://www.e-bahut.com/topic/59249-devoir-maison-de-mathématiques-terminal-st2s/ Dommage que tu ne tiennes pas compte de l'aide que l'on essaye de t'apporter.

Tu n'es même pas venu voir...

2) Si tu as trouvé la valeur minimale à la question 1, répondre à la question 2 est immédiat. Ce n'est pas des maths, tout juste une question de bon sens... 3) En Terminale, calculer la dérivée d'une fonction polynôme ne devrait pas te poser de problème (même si la variable est notée t au lieu de x !). Quelle est cette dérivée f '(t) ?

Bonsoir et bienvenue... Il est presque 19heures, nous sommes dimanche et tu nous demandes de l'aide pour... demain. Est ce bien raisonnable ? Non 😠. Et bien sûr tu n'as RIEN fait pas même les choses simples ou ultra classiques... 1) Si le gâteau doit cuire à 150°C 5% (comprendre 5% de 150 !! ) donc Max ? min ?