C8H10N4O2

Merci pour vos réponses et réflexions très éclairantes !

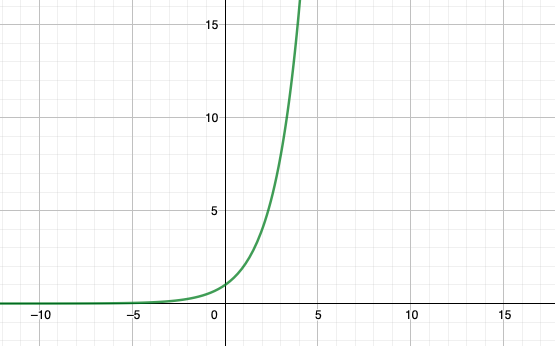
Merci pour vos réponses ! Une manière de reformuler ma question serait de savoir ce que les phénomènes que modélisent les équations différentielles ont de particulier et qui justifie l'introduction de ce nouvel outil. Comment un prof de Terminale décrirait la spécificité du refroidissement d'un corps selon la loi de Newton (ou comme précédemment la croissance d'une population bactérienne) par rapport à d'autres phénomènes que les élèves ont rencontré plus tôt dans leur cursus ? En général lorsqu'on introduit un nouvel outil mathématique, c'est parce que ceux dont on disposait jusqu'alors étaient insuffisants. Par exemple, il me semble assez aisé d'expliquer en quoi les outils de l'Analyse permettent de répondre à des questions qu'on ne peut résoudre avec les seuls outils de l'arithmétique, algèbre, géométrie classique, etc. Donc j'aimerais comprendre de la même manière pourquoi fondamentalement on introduit les équations différentielles. À quelles questions permettent-elles de répondre que les outils connus précédemment ne pouvaient résoudre ? Encore une fois la justification que je retrouve pas mal sur le net : "pour étudier des phénomènes où la vitesse de variation d'une grandeur dépend de la grandeur elle-même" ne me paraît pas très claire ni très spécifique.

Bonjour à tous, Une question me vient à propos des équations différentielles : on dit qu'elles sont un outil pertinent pour modéliser des phénomènes où la vitesse de variation (donc la dérivée) d'une grandeur dépend de la grandeur elle-même. y' = ky est ainsi une équation différentielle simple et on donne parfois comme exemple le cas de la croissance d'une population bactérienne qui double à chaque intervalle de temps donné. Mais à part les fonctions linéaires, toutes les autres fonctions n'ont-elles pas aussi une dérivée qui dépend de la fonction elle-même ? Et pourtant on n'invoque pas pour autant les équations différentielles ! Si un véhicule accélère de façon non-uniforme, sa vitesse (donc la dérivée de sa position) sera fonction du temps mais aussi de sa position sur la piste, non ? Donc je ne vois pas vraiment la différence avec l'évolution exponentielle d'une population bactérienne : en quoi est-il significatif que le taux de variation en un temps t soit fonction de la taille de la population à cet instant ? Il est avant tout fonction de la variable en abscisse qui est ici le temps, non ? Je suis un peu confus sur la spécificité des équations différentielles et aimerais bien un exemple de phénomène non-linéaire où l'usage des équations différentielles n'est pas pour autant pertinent. Merci d'avance pour vos éclairages !

Merci beaucoup, je coinçais un peu sur la fin. Donc de n/3 1 , il vient n + n/3 n + 1 <=> n + n/3 - 3 n + 1 - 3 <=> Un+1 (n + 1) - 3 , ce qui montre l'hérédité de la proposition. Pour l'initialisation, j'avais effectivement calculé à la main tous les termes jusqu'à U5 mais comme le processus me paraissait laborieux, je me demandais si c'était réellement ce qui était attendu pour cet exercice.

Bonjour à toutes et tous, Voici un petit exercice en théorie simple mais sur lequel je bloque : Soit (Un) la suite définie par U0 = 1 et Un+1 = (1/3)Un + n - 2 Il s'agit de montrer par récurrence que pour tout n 5, Un n - 3 . Alors pour l'initialisation du raisonnement, je suppose qu'il faut montrer que la proposition Un n - 3 est vérifiée pour n = 5 . Comment procéder ? Doit-on nécessairement passer par un tableur ou la calculatrice ? Et pour montrer le caractère héréditaire de la proposition, je suis parti de l'hypothèse Un n - 3 pour aboutir à (1/3)Un + n -2 (4/3)n - 3 <=> Un+1 (4/3)n - 3 , mais je ne suis guère plus avancé... Auriez-vous une idée pour débloquer la situation ? Merci d'avance

Merci beaucoup ! :)

Bonjour à tous, La partie A a été corrigée plus haut. Pour la partie B, le 1) se déduit directement du 2)c. de la partie A . Si Un est dans [1/2 ; 1] , alors d'après ce qui précède, f(Un) = Un+1 est aussi dans cet intervalle. Or Uo est dans cet intervalle, donc tous les termes suivants le sont également. En revanche quelqu'un aurait-il une idée pour démontrer la décroissance de la suite dans le 2) ? Merci d'avance.

Bonjour, Une autre manière de poser la question de l'énoncé serait de savoir si les points E et F sont dans le plan ABCD. Si c'est le cas, alors l'auvent et le toit sont bien dans un même plan. Essaie de démontrer par exemple que le vecteur AE est coplanaire des vecteurs AC et AB...

D'accord ! Alors un grand merci de m'avoir accompagné pas à pas dans la résolution de cet exo !🙏 👍 Très bon week-end

Je trouve plutôt A2=(n-2)A + (n-1)In . Simple erreur de signe où ai-je (encore !) fait une erreur ? 😆

Bonjour JulesX et merci d'avoir détaillé les étapes du calcul ! À propos de l'équivalence en vert, je trouve : je suppose qu'on introduit nA=nA.In à droite de l'égalité simplement pour obtenir la factorisation (2-n)*A*In c'est bien cela ?

Je n'ai pas trouvé de réponse satisfaisante concernant ce qu'on pouvait déduire (au niveau Terminale) du fait que les matrices de rotation admettent un déterminant égal à 1. Tous les éléments de réponse trouvés sur le web font appel à des concepts vus au minimum à bac+2 🤨

Là j'avoue ne pas très bien saisir ce que signifie dans ce contexte : "il faut qu'il reste un terme de type matrice" 🤔 Quelle erreur ai-je commis dans ma démarche ? Comment obtient-on alors (n-1)I=A[A+(2-n)I] à partir de n(A+I)=A²+2*A*I+I ? D'accord merci ! 👍

Je trouve donc A2 = n(A + In)- 2AIn-In . Est-ce bien correct ou y a-t-il meilleure manière de présenter A2 ? Ensuite je trouve une égalité légèrement différente de la votre : n(A+In) = A2+2AIn+In donne : nA + nIn = A2+2AIn+In <=> nIn-In = A2+2AIn-nA <=> (n-1)In = A(A + 2In - n)

Ok, donc écrire ceci pourrait suffire comme justification ?

D'accord, c'est compliqué pour la récurrence, mais dans ce cas, quelle démonstration utiliser ? Par ailleurs je modifie mon début de raisonnement du message précédent :

Merci ! Je ne vois pas très bien pourquoi faire appel à la transposée ici... Le début d'une démonstration par récurrence pourrait-il être : ?

Bonjour JulesX et merci pour cette réponse, Alors pour le 1), je comprends que Mais je ne comprends pas comment on obtient U2=n*U 🤔

Oui merci Pzorba, j'ai déjà fait l'exo ! 😄 Ma question portait uniquement sur le sens de la question 4.a) : je tendrais à répondre que comme le déterminant vaut 1, alors les matrices rotation admettent toujours une matrice inverse. Mais la question porte sur "rotations" et non les "matrices représentant une rotation" , donc je me demandais juste si c'était bien la réponse attendue ici...

Bonjour à tous, Toujours sur le thème des matrices que je ne maîtrise que partiellement, j'aurais besoin de votre aide pour cet exo : je ne vois pas comment calculer A2 ...🤔 Merci d'avance !

Bonjour à tous, Dans cet exercice À la question 4.a) j'aurais été tenté de répondre que det(Rtheta) = 1 et que donc toutes les matrices rotation admettent une matrice inverse (dont on peut donner la forme générale). Mais la question porte sur les rotations et non sur les matrices rotation. Pensez-vous que ce soit néanmoins la réponse attendue ? Merci d'avance !

Oui effectivement, ces évènements étant disjoints (= incompatibles) ils ne peuvent se produire simultanément donc p(A inter B) = 0 Par conséquent, la formule générale de p(A U B) donne bien p(A) + p(B).

Bonsoir, oui effectivement, on s'en sort à partir d'une solution particulière, je comprends le raisonnement. Merci JulesX ! 🙂

Bonsoir à tous, Dans le corrigé de ce problème, je ne comprends pas comment on passe de la solution particulière u = -2000 à la solution générale h = -2000 - 13k Quelqu'un saurait-il me l'expliquer ? Merci d'avance !

Si A = M500 < -0,4 et B = M500 > 0,4 , ce sont même deux évènements incompatibles, non ? C'est une bonne question. Comment déterminer s'il s'agit bien d'évènements indépendants ? Et que devient p(A U B) si c'est bien le cas ? 🤔