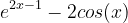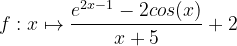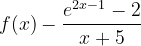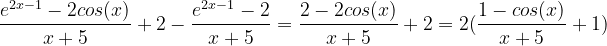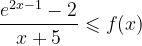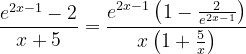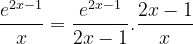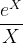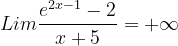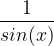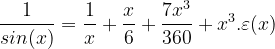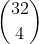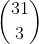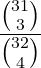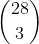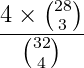C8H10N4O2

C'est manifestement le cas mais les énoncés de ce niveau parlent en général dans ce cas de figure de conjecture et on rencontre davantage cet aspect en début d'exercice habituellement. Là il est demandé de "déterminer" les limites autour de -5 . Étrange, on ne demande normalement pas à un élève de justifier un raisonnement sur les limites en utilisant une valeur approchée d'une expression, à moins de l'avoir précisément guidé dans ce sens...

Il s'agit de l'exo n°100 ici : https://www.lelivrescolaire.fr/page/6971062

Oui c'est ce que je me disais mais c'est étonnant car je tire cette question d'un exo a priori destiné à des élèves de Terminale...

Merci pzorba, Question subsidiaire : comment montrer lors de la recherche de la limite de la fonction en - 5 que est négatif pour x = -5 ? On peut bien sûr le déterminer à la calculatrice mais je doute que ce soit la méthode attendue... 🤔

Bonjour à tous, J'aurais aimé avoir votre avis sur les deux questions ci-dessous : la méthode que j'emploie est-elle la bonne, peut-on faire plus simplement ? Soit f définie pour x différent de -5 1) Justifier que pour x -5 , Voici mon raisonnement : = On montre que 0 1-cos(x) 2 et on a par hypothèse x+5 0 . Donc l'expression est positive, ce qu'il fallait démontrer. 2) En déduire la limite de la fonction f en (factorisation possible car ni l'exponentielle ni x ne sont nuls, entre parenthèses tout tend vers 1 en l'infini) Or, . Le premier facteur est de type et tend vers l'infini, le second tend vers 2 . Au final, , par comparaison f tend donc aussi vers Qu'en pensez- vous ?

Je suis bien d'accord. Je code assez correctement en C depuis des années et je balbutie en Python donc l'univers du code ne me rebute pas a priori mais je dois dire que la "learning curve" pour utiliser les IDE comme Pycharm est très raide. C'est l'utilisation de ces plateformes qui met entre le débutant et l'écriture de programmes informatiques une distance infranchissable, bien plus que le langage de programmation en lui-même... Passer d'Algobox à Pycharm pour un élève de Lycée me paraît une bonne recette pour le dégoûter à vie de la programmation. D'où le caractère précieux d'initiatives comme Edupython ou Thonny (belle découverte), qui permettent de se concentrer rapidement sur la logique des algorithmes plutôt que sur les subtilités de l'interface. Un éditeur de texte, un terminal de commande et en avant !

Très bonne ressource pour les utilisateurs de Mac 👍 Edupython est avant tout destiné à Windows et les IDE comme Pycharm me semblent d'une complexité vite rédhibitoire pour le débutant.

Bonjour, Pour la question 1, tu peux directement calculer p(x 69) avec ta calculatrice en sélectionnant l'option loi binomiale FRép (fonction de répartition). Sinon comme le suggère pzorba, l'événement contraire est que l'avion soit plein, soit X = 70 . Dans ce cas, la formule du cours donne p(X = 70) = 0,9570 . La probabilité recherchée est donc 1 - 0,9570 Pour la question 2, n = 80 et tu dois calculer p(x 69) et p(x 71) = 1 - p(x 70) La question 3 te demande simplement de comprendre que la compagnie doit dédommager les passagers surbookés donc retrancher les indemnités versées de sa recette

Bonjour, Pour la question 6, il convient de déterminer si la fonction admet la même limite de part et d'autre de la valeur où elle est discontinue. Si c'est le cas alors elle peut être "prolongée par continuité" . Pour info, arctan(u) tend vers pi/2 quand u tend vers l'infini positif et vers -pi/2 quand u tend vers l'infini négatif.

Ah oui très juste, c'est une erreur de ma part. Merci de l'avoir relevée

Pas nécessairement. Je les ai mises ici uniquement pour la clarté de la réponse et bien distinguer les fractions.

Bonjour , c'est très simple : la première étape de résolution d'un problème consiste à attribuer un symbole (une lettre qui est souvent x ou y ou encore z) à l'inconnue (la grandeur que l'on cherche à déterminer). Ici l'inconnue est le prix du billet. Appelons-le par la variable x. Ensuite traduisons l'énoncé en langage mathématique : Part payée par Marc : (1/8) x. Part payée par Fabrice : (1/6) x Reste donc : x - ((1/8)x + (1/6)x) = x - ( (3/24)x + (4/24)x ) = x - (7/24)x = (24/24)x - (7/24)x = (17/24)x Donc la part payée par Bruno est : (1/5)* (17/24)x = (17/120)x 1) Celle payée par Boris correspond à 4/5 du reste à payer (puisque Bruno en a déjà payé 1/5 ) Elle est donc de : (4/5) * (17/24)x = (68/120)x = (17/30)x 2) Gain remporté par Marc : (1/8)*15000 Gain remporté par Fabrice : (1/6)*15000 Gain remporté par Bruno : (17/24)*15000 Gain remporté par Boris : (17/30)*15000

Remarque très juste. J'ai un peu de mal avec les D.L. de ce type. D'après la définition fondamentale d'un développement limité, chaque monôme de la partie polynomiale doit être un infiniment petit d'ordre supérieur au monôme qui le précède. Donc ce genre de terme infini me froisse un peu, car cette règle n'est alors plus respectée. Mais d'après ce que je comprends, c'est le mieux que l'on puisse faire pour élargir le concept de D.L. à ce type de fonction. Merci pour cette réponse et bon dimanche.

Bonsoir à tous, J'ai une petite question concernant le DL au voisinage de a d'une fonction qui tend vers l'infini quand x -> a . Par exemple le DL en 0 de . Je lis dans mon manuel que l'emploi de la formule de Taylor permettant de déterminer les coefficients de la partie polynomiale à partir des dérivées successives en 0 n'est pas possible car on a f(0) qui tend vers l'infini. Ça me paraît effectivement éliminer cette méthode. En effectuant la division ploynomiale de 1 par le DL de sin(x) au voisinage de 0 , on obtient : Je comprends la démarche mais voilà ma question : en quoi le problème est-il réglé puisqu'on se retrouve quand même avec le 1er terme (1/x) qui tend vers l'infini quand x ->0 ? 🤔 En quoi la présence d'un infini est ici acceptable alors que tous les monômes du DL sont censés être des infiniments petits en 0 ? Si vous avec une opinion sur la question, je suis tout ouïe !

Bonjour, Soit x la longueur du rectangle et A son aire. Sa largeur est donnée : 20m . Rappel : l'aire d'un rectangle est donnée par le produit de sa longueur par sa largeur. D'après l'énoncé, A = 20x et A = 25(x - 16) On résout donc : 20x = 25(x - 16) <=> 20x = 25x - 400 <=> 5x = 400 <=> x = 80 La longueur du rectangle est de 80m

Bonjour, La condition dont parle l'énoncé est que pour qu'un triangle puisse être construit, chacun de ses côtés doit être inférieur à la somme des deux autres. Autrement dit, on doit vérifier simultanément : AB < AC + BC , AC < AB + BC et BC < AB + AC . Tu dois traduire ces conditions sous forme d'inéquations et les résoudre. Par ailleurs, AB, AC et BC étant des longueurs, ce sont des nombres positifs, ce qui impose aussi une contrainte sur x . Ex : puisque AB > 0 , on a nécessairement x + 2 > 0 donc x > -2 Idem pour les deux autres côtés.

Merci de cette réponse, Ça me confirme le résultat d' 1/8 qui me paraissait élevé a priori... Pour la seconde question, il s'agit de déterminer la probabilité d'avoir exactement un as dans une main de 4 cartes. Mon calcul consiste à dénombrer les combinaisons de 3 cartes parmi 28 puis de multiplier le résultat par 4 car toutes ces combinaisons peuvent se voir accompagnées de chacun des 4 as.

Bonjour Pzorba, Doit-on vraiment multiplier par 1/32 ? 🤔 Il n'y a qu'une manière d'obtenir l'as de pique donc le nombre de cas favorables est à mon sens 1 x binom(31;3) . On divise ensuite par le nombre total de cas possibles, à savoir binom(32;4) .

Bonjour à tous, J'aimerais calculer la probabilité pour un joueur de recevoir l'as de pique lorsqu'on distribue à chacun des joueurs 4 cartes prises dans un paquet de 32 cartes. Le nombre total de mains possibles correspond aux combinaisons de 4 éléments parmi 32 : Pour calculer le nombre de cas favorables, je me dis que si j'ai l'as de pique, reste à déterminer le nombre de combinaisons de 3 cartes parmi 31 restantes : = . Ça me paraît beaucoup : a-t-on vraiment une chance sur huit d'avoir l'as de pique ? De même pour calculer la probabilité de recevoir un des quatre as : Si on a un as, reste à choisir 3 cartes parmi 28 (les cartes qui ne sont pas des as). Comme il y a 4 as, le nombre de cas favorables est 4 x La probabilité est donc de = Ces calculs vous paraissent-ils corrects ? Merci d'avance

Ce serait 15^4 uniquement si le code pouvait être composé de 4 lettres : AAAA par exemple. Ici ce n'est pas le cas : il s'agit d'un code à 4 éléments : 1 lettre et 3 chiffres

Non c'est exact, le résultat est bien de 20 000 . Ma question était de savoir si on pouvait obtenir celui-ci plus directement que par la méthode que je présentais mais manifestement non puisque c'est peu ou prou la même que celle-ci. Merci de cette réponse en tout cas !

Les membres de ce forum auraient été ravis de t'aider si tu avais pris le soin de solliciter leur assistance avec un minimum de courtoisie. Manifestement l'urgence pour toi n'est pas en mathématiques mais en savoir-vivre, dont tu sembles ignorer les bases les plus élémentaires. Tu verras, c'est un pré-requis indispensable dans la vie, en particulier pour communiquer avec des gens dont tu souhaites qu'ils t'apportent leur aide. Allez, fais un petit effort la prochaine fois et tu as déjà pas mal d'éléments pour rendre une copie correcte pour ce DM. Bonne soirée

Tu exagères, tous les éléments sont dans les corrigés cités plus haut. Pour la partie 1) il s'agit simplement de calculer des images par f donc de remplacer t par les heures en question dans la formule de f(t) et ainsi obtenir les hauteurs d'eau. Pour la partie 2) voici ce qu'indique le tableur :

Au temps pour moi, je me suis mal exprimé : le code à 4 éléments comporte une seule lettre (parmi les 5 premières de l'alphabet) et 3 chiffres (de 0 à 9).

Bonjour à tous, Pour déterminer le nombre de codes à 4 éléments (pour un digicode par exemple) que l'on peut former avec une lettre (parmi les 5 premières de l'alphabet) et 10 chiffres (de 0 à 9), j'ai supposé qu'on choisissait d'abord la lettre puis successivement 3 chiffres donc 5x10x10x10 = 5 000 codes possibles formés d'une lettre suivie de 3 chiffres. Puis étant donné que la lettre peut en réalité occuper 4 places distinctes dans le code, chacun des 5000 codes en donne 4 en changeant la place de la lettre. J'ai donc multiplié le tout par 4 pour obtenir un total de 20 000 codes possibles. Existe-t-il une autre manière (plus directe) de faire ce calcul ? Merci d'avance