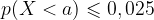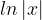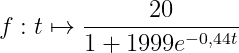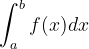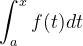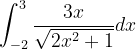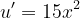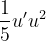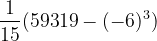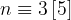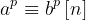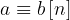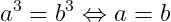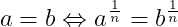C8H10N4O2

oui c'est ce que je me suis dit, mais comment le justifier ? On ne peut pas dire que p(A U B) = p(A) + p(B) , n'est-ce pas ?

Bonjour à tous, Je travaille sur un petit exo sur l'inégalité de concentration et je comprends le corrigé mais pas la dernière démonstration du 2) (signalée en rouge). Quelqu'un pourrait-il me dire d'où vient cette équivalence ? Merci par avance !

Merci à tous pour vos réponses !🙂

Bonjour à tous , J'aimerais comprendre une chose : Lors de l'étude d'une loi de probabilité binomiale, pourquoi doit-on forcément l'exprimer sous la forme lorsqu'on veut utiliser la calculatrice ? (Et non pas p(X > k) par exemple) Ex : soit X une variable qui suit la loi binomiale B(5 ; 0,2) . Pour calculer p(X > 3) , je dois passer par la probabilité de l'évènement contraire et calculer 1 - . Merci d'avance pour vos réponses !

Merci Pzorba, mais je n'ai toujours pas compris la logique derrière l'énoncé de l'exercice. Je connais et pratique pas mal les exos classiques autour de la loi binomiale, dont ceux qui permettent de déterminer un seuil au-delà duquel une condition sur la proba est respectée, mais là je n'arrive pas à comprendre cette histoire de X dans un intervalle... La nuit portant conseil , ça ira peut être mieux demain !

Bonjour à tous, J'ai du mal à comprendre cet énoncé, même après en avoir lu le corrigé (qui consiste essentiellement à faire une liste d'une loi binomiale sur calculatrice). J'arrive à comprendre qu'on veut déterminer a et b tels que . Mais je ne comprends pas en quoi par exemple ça nous conduit à chercher Si quelqu'un pouvait m'expliquer la logique derrière cet exo, je lui en serais très reconnaissant !

Merci, c'est maintenant plus clair ! 🙂

La démonstration est limpide, merci ! 😀 Mais alors pourquoi ça ne "fonctionne pas" avec une valeur arbitraire de x non-nulle, par exemple -6 ? 🤔

Je sais bien , d'où le fait que la formule donne le logarithme de la valeur absolue de x comme étant une primitive de 1/x avec x < 0. Mais avec un exemple concret x = -6 , ça ne fonctionne pas, donc je me demande où est l'erreur...

Bonjour à tous, J'ai une petite question : on dit qu'une primitive de 1/x est : . Mais si je prends x = -6 , ln(6) n'est pas une primitive de 1/(-6) ! Où est l'erreur ? Merci d'avance pour vos réponses !

Merci, document intéressant au demeurant !👍

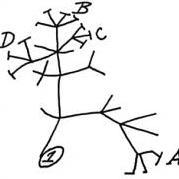
Ça me paraît tout à fait juste, bravo ! Effectivement, en creusant un peu, le modèle de Verhulst est employé pour modéliser des phénomènes exponentiels dans un premier temps puis qui convergent vers une limite (par opposition (en simplifiant) à une exponentielle à l'infini comme le suggère Malthus dans le cadre de la croissance de populations). Cela me semble cohérent avec votre idée. 👍 Post scriptum : mais au fait en quoi le terme en 20-y donne un maximum possible de y=20 ?🤔 Pour info, la fonction solution de l'équation différentielle ci-dessus avec la condition initiale f(0) = 0,01 (10 000 ménages équipés d'un ordinateur en 1980) est : On a bien f(t) qui tend vers 20 quand t tend vers l'infini.

Bonjour à tous, J'ai une petite question : dans un exercice sur les équations différentielles, on propose de modéliser le nombre de ménages équipés d'un ordinateur en France à partir de 1980 par le modèle de Verhulst. D'après ce modèle, f(t) la fonction qui donne ce nombre de ménage, est solution de l'équation y' = 0,022y(20 - y) On trouve à la fin de la résolution de l'exercice que d'après ce modèle, un peu moins de 20 millions de ménages devraient être équipés d'un ordinateur en 2014. Or l'INSEE nous informe qu'en réalité, plus de 22 millions de ménages possédaient un ordinateur en 2014. La question est la suivante : "Expliquer pourquoi l'estimation faite par le modèle de Verhulst est incorrecte" . Avez-vous une idée ? J'avoue que je sèche...🤔

Merci JulesX d'avoir pris le temps de rédiger cette réponse détaillée avec laquelle je suis en grande partie d'accord, en particulier sur le fait qu'il soit discutable de faire le distinguo entre variable de la primitive et variable d'intégration. Pour une intégrale définie de bornes a et b, voici comment je raisonne : cette intégrale désigne l'aire sous la courbe de la fonction f entre les axes x = a et x = b. Si on peut exprimer cette aire sous la forme d'une fonction, c'est précisément parce qu'elle ne prendra pas la même valeur selon la position de la borne supérieure. En d'autres termes, elle est fonction d'une variable et il me semble que cette variable est celle symbolisée par l'axe des abscisses, soit la même variable que celle dont dépend la fonction étudiée. Donc je comprends le souci de ne pas nommer la borne supérieure de la même manière que la variable en abscisse, mais pas tellement le fait de distinguer variable de la primitive et variable d'intégration.

Bonsoir à tous, Comment comprenez vous le concept de variable muette dans le cadre de l'intégration ? Je comprends que lorsqu'on nomme la borne supérieure d'intégration non plus b comme ici : mais x, il existe un risque de confusion et qu'on écrive dès lors : . En revanche, j'ai du mal à comprendre qu'on fasse la distinction entre variable d'une primitive et variable d'intégration comme dans le passage ci-dessous : Si cela vous a déjà intrigué et qu'après y avoir réfléchi, vous avez désormais une vision claire de cette distinction, je suis à l'écoute de vos explications ! Par avance merci

Merci julesx !

Merci Black Jack !

Merci

Merci beaucoup pour ces précisions ! Je bloque sur celle-ci désormais : Y a-t-il une primitives d'une fonction de forme connue à reconnaître ici aussi ?

Donc si j'ai bien compris, ici je pose d'où et je reconnais que l'élément différentiel est de la forme Donc l'intégrale est égale à = = = 3969 Est-ce bien correct ?

Bonsoir à tous, Dans le cadre d'un exo , on me propose le raisonnement suivant : si , alors . Alors autant je sais que entraîne , mais est-ce aussi vrai que ? Sinon comment justifier cette implication ? Merci d'avance pour vos réponses !

Merci à tous les deux pour ces approches complémentaires que je vais m'employer à appliquer. Quoi qu'il en soit, mon intuition de développer tout en un vaste polynôme n'était clairement pas la bonne 😆

Bonjour à tous ! Je souhaiterais avoir votre avis sur la méthode à employer pour calculer l'intégrale : . A priori je partirais pour développer l'expression à intégrer, me ramener à un polynôme et utiliser la primitive , mais n'y a-t-il pas une autre méthode ? Merci d'avance pour vos réponses !

Ma question est la suivante : n'est équivalent à que si a et b sont de même signe. Qu'en est-il pour , avec n un entier quelconque ? Par exemple il me semble que quels que soient a et b. De même si et seulement si a et b sont positifs. Mais qu'en est-il pour ?

Bonjour à tous, Après avoir fait chou blanc à la quête d'une réponse sur internet, je viens vous consulter car je m'interroge sur les règles qui entourent le passage à la puissance n-ième lors de la résolution d'une équation. Par exemple, à quelle condition a-t-on le droit d'écrire : ? Ou encore : Je sais que pour n = 2, a et b doivent être de même signe pour pouvoir écrire la première équivalence , et que a et b doivent être positifs pour pouvoir écrire la seconde. Mais qu'en est-il lorsque n est un entier positif quelconque ? Merci d'avance pour vos lumières !