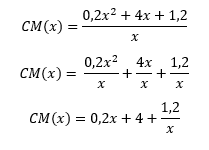PAVE

Pour la question 4, bravo d'avoir repéré l'identité remarquable. Ta conclusion est ambiguë. Quel que soit x strictement positif (ce qui est le cas ici puisque x appartient à ]0;10]) (x-√6)²0 donc CM(x)0,46+4 (environ 4,98) Pour tout x € ]0;10], CM(x) 4,98 donc 0,46+4 4,98 est un minimum !

0.2x*x²/x+1.2/x-0.4V6*x/x0 l'écriture en ligne ne facilite pas la lisibilité 😬 . Écris cela sur papier avec des traits de fraction, tu verras mieux.... 0.2*x²/x+1.2/x-0.4/6*1 x/x0 [0,2x² +1,2- (0,4V6)x] / x 0 [0,2x² - 0,4V6 x +1,2] / x 0 Je te laisse finir....

3. Montrer que résoudre dans ]0; 10] l’inéquation CM(x) CM( √ 6) Tu viens de montrer que cette inéquation s'écrit : 0,2x+4+(1,2/x) 0,46+4 (1) revient à résoudre dans ]0; 10] l’inéquation x² −2 √6x+6 0 (2) . Donc par des transformations régulières (respectant les règles du calcul algébrique ), tu dois "passer de la forme (1) à la forme (2). Pour cela : * tu fais en sorte que le second membre soit 0 * tu réduis le 1er membre * tu observes qu'il y a un dénominateur contenant x, donc mise sous dénominateur commun du 1er membre. Mais je viens de voir qu'Anylor a entamé la procédure. Essaye de finir.

Bon on finit d'abord la question 2... Tu es parvenue à l'égalité suivante : 1,2/√6 = (1,2*√6) /6 = (1,2/6)*√6 = 0,2*√6 donc "cela nous donnerait donc CM(√6)= 0.2*√6+4+(1.2/√6) " =0,2*√6+4+0,2*√6 = √6(0,2+0,2) +4 = 0,4 √6 +4 ce que l'énoncé demandait de démontrer. Tu peux maintenant attaquer la question 3 mais en te servant de cette expression pour CM(√6). NB : là encore tu as dans l'énoncé le résultat à obtenir... ça aide

Oui mais mieux vaut laisser 1,2/6 sous la forme 0,2. Continue.

Efforce -toi d'écrire des ÉGALITÉS. 1,2/√6 = (1,2*√6) /6 Oui bravo : on multiplie le numérateur ET le dénominateur par √6 = (1,2/6)*√6 = ? Tu y es presque 🙂.

Oui. Mais il faut poursuivre le calcul jusqu'à obtenir... 0,4 √ 6+4. En 3ème, tu as du apprendre qu'on ne laisse pas un dénominateur avec un "radical" (une racine carrée). Donc il te faut écrire (1.2/√6) sous une autre forme... Essaye...

Ce que tu as écrit n'est pas faux mais n'a pas la forme attendue par l'énoncé (qui une fois de plus te donne... la réponse !!) Par ailleurs tu n'as pas suivi mon conseil : Pour aboutir à la forme donnée par l'énoncé : 2. Montrer que CM( √ 6) = 0,4 √ 6+4, il serait plus simple que tu suives mon conseil .

Dans l'expression que tu viens d'obtenir pour CM(x), si tu remplaces x par 6, tu vas obtenir bien sûr CM(6)... A toi de faire...

pourtant l'énoncé te donne la... réponse 🤔

CM(x) = (0,2x²+4x+1,2) / x rappel : souviens toi que (a+b)/c = (a/c)+(b/c) d'où CM(x) = ......

Non, cette écriture est fausse. On a un quotient dont le numérateur est 0,2x²+4x+1,2 et dont le dénominateur est x. Quand on écrit un tel quotient "en ligne", il FAUT absolument mettre des parenthèses autour du numérateur (voire du dénominateur parfois). CM(x) = (0,2x²+4x+1,2) / x NB a+b/c est égal à a+(b/c) (la division est prioritaire sur l'addition) ==> 3+5/2 = 3+2,5 = 5,5 à ne pas confondre avec (a+b)/c = (a/c)+(b/c)==>(3+5)/2 = 8/2 = 4

Je t'ai dit NON et tu fais quand même....

Non, ce n'est pas ce que j'ai écrit.

Bonjour, Ici ou ailleurs, j'ai déjà vu, il y a peu, cet énoncé mais il y manquait l'expression de C(x)😟. Bon alors... voyons !! Tu aurais pu au moins faire les premières questions... 1) D'après l'énoncé, on a : C(x) = 0,2x² +4x+1,2 et CM(x)=C(x)/x Il suffit de remplacer dans la définition de CM(x), C(x) par son expression... Essaye et souviens toi que (a+b)/c = (a/c)+(b/c)

Essai d'écriture en LaTex (\dfrac{1+x}{\dfrac{1}{x²}+3}\)

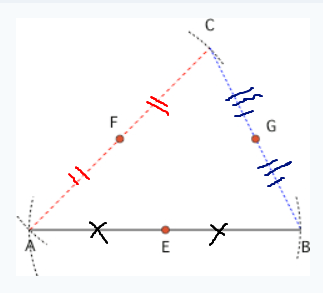
La "figure ci-contre" de ton énoncé ressemble-t-elle à celle-ci où les points E, F et G sont les milieux des segments [AB], [AC] et [CB] ?

Bonjour, Avec la figure et en prime un énoncé complet, on serait plus à même de pouvoir t'aider.... Ceci dit, si la figure correspond à ce qui précède dans ce fil ancien.... tout est dit 🤓. EDIT : Je viens d'observer que tu es en Sixième. Montre nous la figure de ton énoncé, on va t'aider... Pour une élève de Sixième, il y a peut-être encore des choses... à te dire.

Bonjour Laura, D'accord pour les questions 1 et 2. Je te recommande de rédiger tes réponses en justifiant ce que tu fais : * dire que f(x) est un polynôme du second degré (forme ax²+bx+c) * on appelle racine d'un polynôme une valeur de x qui annule ce polynôme donc on calcule f(5) puis f(40) etc. * forme factorisée d'un trinôme du second degré dont on connait les racines x1 et x2 : f(x) = a (x-x1)(x-x2) Pour la question 3, : On étudie le signe de chaque facteur dans la forme factorisée puis tableau de signes. Question 4 : Dans ton cours tu dois trouver (et apprendre !!) pour quelle valeur de x, on a un max ou un min (on peut vérifier graphiquement en regardant le sommet de la parabole) etc... A toi de faire et de dire... si tu veux.

Bonjour, Ton problème relève prioritairement de la physique... essaye sur la partie physique du site, cela sera plus sûr🤓 ! Avec mes souvenirs de jeunesse !!, j'ai dessiné ce qui suit. et un peu de pub pour Agco 👩‍🌾

Bonsoir à vous deux, Pour illustrer et surtout pour rêver de voyages lointains😢

Il y avait longtemps que je ne m'étais pas "amusé" avec le logiciel SCRATCH 😃 Si tu as déjà un peu utilisé SCRATCH et si tu as installé ce logiciel sur ton ordinateur, tu pourras essayer de faire fonctionner les scripts donnés par l'énoncé...🏋️‍♂️

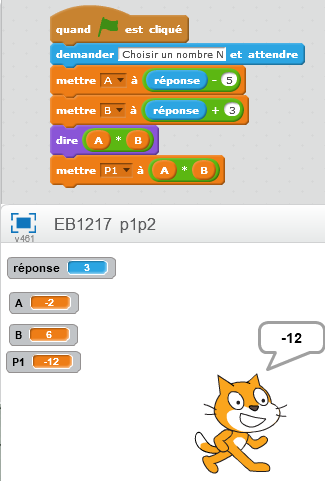
Bonsoir, Tiens du Scratch 🤓 !! En fait Scratch ici ne sert que de décor... Je te "traduis" en langage courant le premier script : On choisit un nombre (celui que l'on veut !!) On retranche 5 à ce nombre et on appelle A le résultat obtenu. Ensuite on ajoute 3 au nombre choisi au départ et on appelle B la somme obtenue. Enfin on multiplie entre eux les nombres A et B. PREMIER CAS ÉTUDIÉ Si on choisit comme nombre de départ le nombre 2, * que vaut A ? * que vaut B ? * Que vaut A*B ? (* signifie "multiplié par" ; * remplace le signe habituel de la multiplication) A toi de Dire....

Oui mais bonjour la galère pour la saisie... Pour accompagner ma tite-fille, j'ai fait l'essai avec une Tite calculatrice. Je suis bien vite revenu à mon clavier d'ordinateur. Le site "jaicompris.com" permet d'accéder facilement à Trinket mais il y a bien d'autres possibilités ?. J'ai commencé avec Edupython et sa doc. Coucou, Laura ?️‍♂️.