virgule2142

mon prof de maths fait des équation 12=..... 11= ....... mais pas a= ou b=. sans commentaire je suis content. merci pour la confirmation

12=(2x+1)2-4x-2+(4x2-1) 12=(2x+1)(2x+1)-2(2x+1)+(2x-1)(2x+1) 12=(2x+1)(2x+1-2+2x-1) 12=(2x+1)(4x-2) 12=2(2x+1)(2x-1) je pense avoir réussi.

Bonjour a tous je suis encore sur mes exo de factorisation .je post à nouveau un calcul en espérant avoir juste. Factoriser au maximum : 12=(2x+1)2-4x-2+(4x2-1) 12=4x2+4x+1-4x-2+(2x-1)(2x+1) 12=4x2+4x+1-2(2x-1)+(2x-1)(2x+1) 12=(2x-1)(4x2+4x+1-2+2x+1) 12=(2x-1)(4x2+6x) j ai bien identifié deux identités remarquables (2x+1)2 et (4x2-1). Mon déroulement me semble juste mais mon résultat est faux (2(2x+1)(2x−1) est le résultat trouvé sur des factorisation en ligne). Je pense que c est le passage de la 3eme ligne a la 4eme qui est faux mais j'arrive pas a corriger l’erreur. Dit le moi si je post trop ici.

merci mais la mon cerveau a bloqué en lisant tes explications. Je continu mes exercices sur la factorisation. j hésite a poste qqch ici tout les jours pour vérifier si mes calculs sont bons

merci pour la confirmation et la belle démonstration.

Pouvez vous me confirmer (3-5x)²=(3-5x)(3-5x) et (3+5x)2=(3+5)(3+5x) car je pensais que (3-5x)² =(3-5x)(3+5x). J'avais pas compris comment reconnaître un facteur commun et pourtant la définition est simple. Merci beaucoup je vais bien verrouiller toutes ces notions dans mon esprit. Pas facile les maths me je m accroche. merci encore de m' avoir répondu aussi tard.

b=(5x-3)(x+1)+6x-10x2+(3-5x)2 b=-(3-5x)(x+1)+2x(3-5x)+(3-5x)(3+5x) b=(3-5x)(-x-1-2x-3-5x) b=(3-5x)(-8x-4) b=-4(3-5x)(2x-1) voila je pense avoir bien appliqué vos conseils et j ai vérifié les changements de signes à la troisième ligne.

merci beaucoup pour vos explications très détaillées. je comprend un peu mieux. je refais b

j ai refait la b b=(5x-3)(x+1)+6x-10x2+(3-5x)2 b=-(3-5x)(x+1)+2x(3-5x)+(3-5x)2 b=(3-5x)[(x-1)-2x(3+5x)-(3+5x)2] b=(3+5x)[x-1-6x-10x2-9+25x2] b=(3+5x)(15x2-5x-10) b=5(3-5x)(3x2-x-2) je pense avoir trouvé la bonne réponse. J'attend vos avis. Merci d'avance de prendre de votre temps pour me répondre

a=9x2+12x+4-2x*(3x+2)+(4-9x2) a=(3x+2)2-2x(3x+2)+(2-3x)(2+3x) a=(3x+2)[-2x(3x+2)+(2-3x)(2+3x) a=(3x+2)[(-6x2-4x)+(2-3x)(2+3x)] a=(3x+2)(-15x2-4x+4) je suis sur que c est un mauvais résultat mais j'arrive pas à faire mieux. b=(5x-3)(x+1)+6x-10x2+(3-5x)2 b=-(3-5x)(x+1)+2x(3-5x)+(3-5x)2 b=(3-5x)[x-1-2x(3+5x)-9+25x2] b=(3-5x)(x-1-6x+15x2-9+25x2) b=(3-5x)(40x2-5x-10) b= 5(3-5x)(8x2-x-2) je pense avoir bon. J'attend vos avis éclairés

mon profil est modifié je suis en second et les maths c est vraiment une galère depuis longtemps. j'essai autant que faire ce peux de progresser . j ai bien lu vos réponses et je vais refaire mes calculs. merci d avoir pris le temps de me répondre

Bonjour je fait un nouveau post mais je ne veux pas polluer le forum si administrateur me demande de continuer ma demande d aide avec celui du 26/10 je le ferai. Merci beaucoup aux deux personnes qui m ont aidé pour mon problème de maths. je pense avoir réussi ces deux expressions ou il faut factoriser au maximum : a=9x2+12x+4-2x*(3x+2)+(4-9x2) a=(9x2+12x+4)-(6x2+4x)+(-9x2+4) a=(3x2+8x+4)+(-9x2+4) a=-6x2+8x+8 a=-2(3x+2)(x-2) b=(5x-3)(x+1)+6x-10x2+(3-5x)2 b=(5x-3)(x+1)+6x-10x2(-5x+3)2 b=(5x2+2x-3)+6x-10x2+(25x2-30x+9) b=(5x2+8x-3)-10x2+(25x2-30x+9) b=(-5x2+8x-3)+(25x2-30x+9) b=20x2-22x+6 b=2(5x-3)(2x-1) voila je pense avoir deux résultats corrects et avoir factorisé au maximum pour ces deux expressions. merci d avance pour votre aide

merci pour l'aide car il faut que je factorise au maximum .

a= 3(4-x)2+(x+2)(x-4) a=3[-1(x-4)*-1(x-4)]2+(x+2)(x-4) a=3(x-4)2+(x+2)(x-4) a=(x-4)[3(x-4)+(x+2)] a=(x-4)(4x-10) la je pense avoir réussi.

ok je corrige merci pour l indice facteur de 3

a= 3(4-x)2+(x+2)(x-4) a=3[-1(x-4)*-1(x-4)]2+(x+2)(x-4) a=3(x-4)2+(x+2)(x-4) a=(x-4)*(3+x+2) a=(x-4)*(x+5) grâce à votre aide j'ai peut être enfin réussi. les deux "-1" qui deviennent c'est une vrai faute d inattention.

merci beaucoup c est plus clair pour moi. je refais le calcul

merci pour votre aide. j ai refait mon opération a= 3(4-x)2+(x+2)(x-4) a=3*[-1(x-4)]2+[(x+2)(x-4)] a=(x-4)*[-1(3+x+2)]2 a=(x-4)*(-x-5)2 je ne suis pas sur de moi car je ne sais pas si mon placement de la puissance 2 à la troisième lignes est correct.

a= 3(4-x)2+(x+2)(x-4) a=3[-1(x-4)*-1(x-4)]+(x+2)(x-4) a=(x-4)*[-1*(3+x+2)] a= (x-4)*(-x-5) j'ai refait mon opération . je pense avoir un résultat correct.

merci pour votre réponse donc le facteur commun serai (x-4). je refait mon calcul

Bonjour je n'arrive pas à trouver la solution à une expression que je dois factoriser au maximum. a= 3(4-x)2+(x+2)(x-4) je sais qu il faut trouver un facteur commun mais je ne sais pas comment transformer (x-4) en (4-x) qui est le facteur commun de cette expression. J'ai beau chercher dans mes cours je n'arrive pas à trouver la solution . Si quel qu'un pouvez m'expliquer ou me donner un lien vers la méthode. Merci d'avance

merci pour le tableau. J'ai encore une fois pu terminer mon exercice avec vos précieux conseils. Je vais recommander ce site à mes amis qui ont des grosses difficultés comme moi en maths. Je vous souhaite une excellente fin de journée.

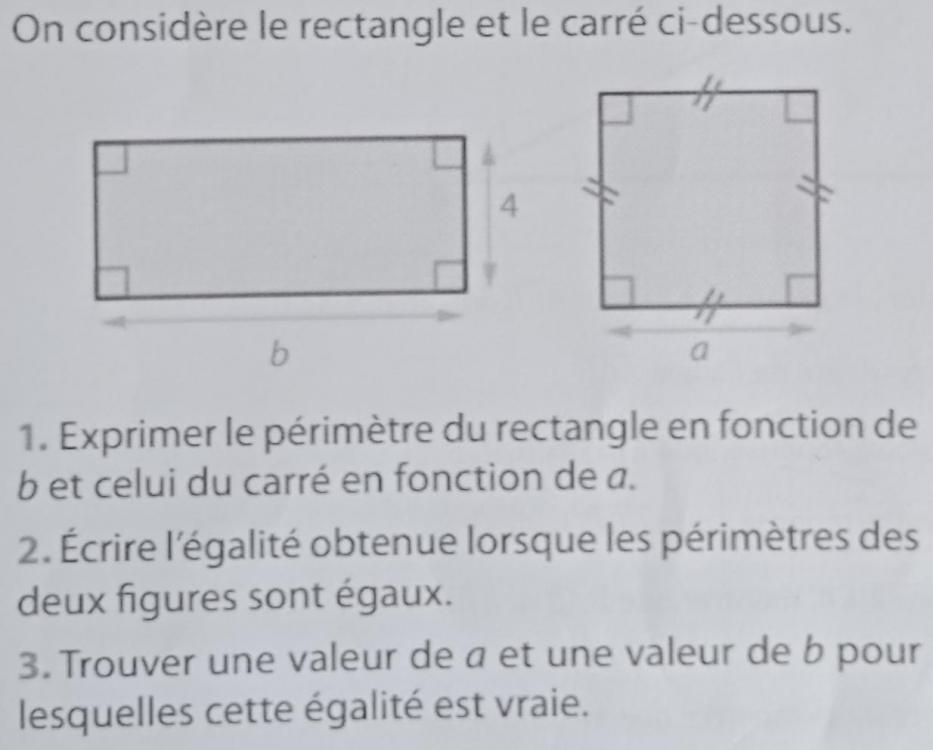
Merci pour vos conseils. J'ai un doute sur la justification du choix de la valeur de a et sur ma conclusion. 3)On sait qu'une égalité est constituée de deux membres séparés par un signe =. Une égalité est vraie quand les deux membres ont la même valeur. on veux tester l'égalité de (4+b)*2=4*a Si a=7 on a (4+b)*2=4*7 (4+b)*2=28 4+b=28/2 4+b=14 b=14-4 b=10 on peux en déduire que si a= 7, b=10. Les deux membres sont égaux donc cette égalité est vraie.

Bonjour, J'ai fait mon exercice mais je ne sais pas si j'ai trouvé les bonnes réponses. Pouvez vous m'aider. 1)La formule pour calculer le périmètre du rectangle est (l+L)*2. On peux donc écrire (4+b)*2. La formule pour calculer le périmètre d'un carré est C*4. On peux donc écrire a*4. 2) L'égalité obtenue lorsque les périmètres des deux figures sont égaux est (4+b)*2=a*4 . 3)Pour dire que cette égalité est vraie nous donnons a =5 et b=6. Ce qui donne (4+6)*2=5*4 10*2=20 20=20 Les valeurs choisies pour a et b sont donc correctes pour validée cette égalité.

Je vous remercie beaucoup. Sans vos conseils je n'aurai pas réussi à trouver les bonnes réponses. C'est bien de ne pas m'avoir donné directement les réponses.