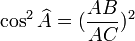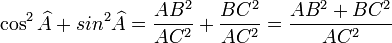Trigonométrie : relations trigonométriques
La tangente comme quotient
On a pour toute mesure x (differente de
et de 
) d'un angle : 
Démonstration
On a vu que
Ainsi
donc pour tout angle x différent de et de (car 
) , on a :
Il manque les angles obtus!!
Ainsi donc pour tout angle x différent de et de (car ) , on a : Il manque les angles obtus!!
On a vu que
Ainsi
donc pour tout angle x différent de et de (car ) , on a :
Il manque les angles obtus!!
Ainsi donc pour tout angle x différent de et de (car ) , on a : Il manque les angles obtus!!
Exemple
Sachant que
et
, calculer une valeur approchée de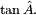 
Solution
Formule liant cosinus et sinus
On a pour toute mesure x d'un angle :
Démonstration
[modifier] Méthode analytique
On a vu que
Dans un triangle rectangle, le carré de l'hypothénuse est égal à la somme des carrés des deux autres côtés
On a AB2 + BC2 = AC2 et donc
Ainsi
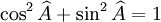
Elargissons, car en effet pour tout , cos2x > = 0 et sin2x > = 0
et... pour tout , cos2x + sin2x = 1
[modifier] Méthode trigonométrique
Le triangle trigonométrique montrant les rapports entre sinus et cosinus Sur le cercle trigonometrique ci contre , on peut utiliser Le théorème de PythagoreCe dernier stipulant que
Dans un triangle rectangle, le carré de l'hypothénuse est égal à la somme des carrés des deux autres côtés
Ainsi cela se traduit par :
AD2 + CD2 = AC2
Or, ici
- AC = 1
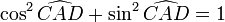
Elargissons, car en effet pour tout ,
et 
et... pour tout , cos2x + sin2x = 1
Méthode analytique
On a vu que
Dans un triangle rectangle, le carré de l'hypothénuse est égal à la somme des carrés des deux autres côtés
On a AB2 + BC2 = AC2 et donc
Ainsi
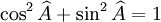
Elargissons, car en effet pour tout , cos2x > = 0 et sin2x > = 0
et... pour tout , cos2x + sin2x = 1
Méthode trigonométrique
Le triangle trigonométrique montrant les rapports entre sinus et cosinus Sur le cercle trigonometrique ci contre , on peut utiliser Le théorème de Pythagore
Ce dernier stipulant que
Dans un triangle rectangle, le carré de l'hypothénuse est égal à la somme des carrés des deux autres côtés
Ainsi cela se traduit par :
AD2 + CD2 = AC2
Or, ici
- AC = 1
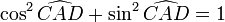
Elargissons, car en effet pour tout ,
et et... pour tout , cos2x + sin2x = 1
Exemple: Calcul du sinus à partir du cosinus
Sachant que
, calculer une valeur exacte de sinxSolution
On a la formule :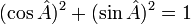 
donc :
donc :
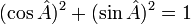
donc :
donc :
Propriétés des arc associés
On montre aisément, à l'aide de symétries, les propriétés suivantes.
![Image IPB](http://"http://fr.wikiversity.org/wiki/Image:Trigo_arc_supp.svg")
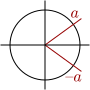
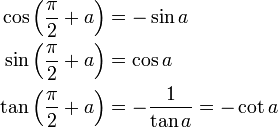
Formules de trigonométrie
Nous démontrerons en annexe 3 les formulaires ci-dessous sur les fonctions circulaires sin, cos et tan.
Soient a et b deux réels.
Formulaire 1 : addition
Formulaire 2 : duplication
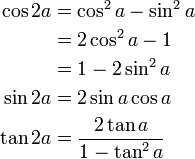
Formulaire 3 : linéarisation (formules de Carnot)
Formulaire 4 : produit-somme
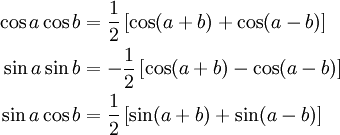<a name="Formulaire_5_:_somme-produit_.28formules_de_Simpson.29" id="Formulaire_5_:_somme-produit_.28formules_de_Simpson.29">Formulaire 5 : somme-produit (formules de Simpson)
Sources : http://fr.wikiversity.org