Barycentre de 3 points ou plus
Définition
Soient A, B et C trois points de l'espace. Soient α, β et γ trois réels vérifiant
. Le barycentre du système de points pondérés {(A,α);(B,β),(C,γ)} est l'unique point G qui vérifie
Si α + β + γ = 0, le barycentre n'existe pas.
Cette définition est fondamentale car elle est le point de départ de nombreux exercices sur les barycentres Exemple
Soit G le centre de gravité de ABC. G est le barycentre du système de points pondérés {(A,1);(B,1);(C,1)}.
Localisation
Soit G le barycentre du système de points pondérés {(A,α);(B,β);(C,γ)} (avec
). On peut trouver l'emplacement de G par les trois formules suivantes : 
, 
et 
. Le principe de la démonstration qui suit est important : si l'on veut obtenir la localisation de G à partir de A, il faut utiliser la relation de Chasles pour faire apparaître A au milieu de tous les vecteurs où il n'est pas déjà. Démonstration
donc
donc
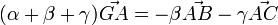
donc
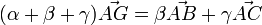
Finalement
, d'où la nécessité d'avoir On démontre les autres égalités de la même manière.
Propriétés
On suppose désormais que le barycentre G du système de points pondérés {(A,α);(B,β);(C,γ)} existe, c'est-à-dire
Coplanarité
Propriété
Comme
, alors 
Invariance par multiplication par un réel non nul
Propriété
Soit k un réel non nul. Le barycentre de trois points pondérés ne change pas si on multiplie tous les coefficients par k.
Démonstration
donc 
De plus, comme
et que , on a bien 
Donc G est le barycentre du système de points pondérés {(A,kα);(B,kβ);(C,kγ)}
Égalité valable en tout point de l'espace
Propriété
Pour tout point M de l'espace :
Le principe de la démonstration qui suit est important : la relation de Chasles permet d'introduire un nouveau point dans la formule de définition. Cette idée revient souvent dans les exercices de ce type. Intérêts :
- Ramener un problème mettant en jeu plusieurs points (A,B,C) à un problème mettant en jeu un seul point (G)
- Calculer explicitement les coordonnées du barycentre en faisant M=O
Démonstration
Soit M un point de l'espace
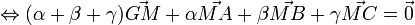
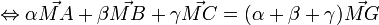
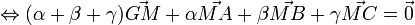
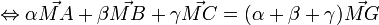
Coordonnées du barycentre
Propriété
On munit l'espace d'un repère
dans lequel A(xA,yA,zA), B(xB,yB,zB) et C(xC,yC,zC)Les coordonnées de G dans
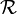sont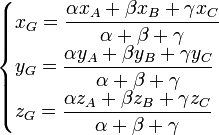 
Démonstration
On sait que pour tout point M de l'espace, 
.
On applique cette formule en O :
donc
donc, comme O est le centre du repère, 
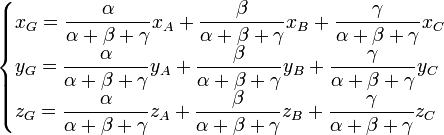, ce qui est le résultat
.On applique cette formule en O :
donc
donc, comme O est le centre du repère
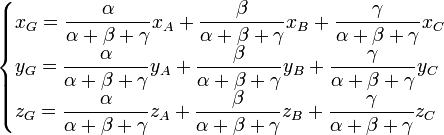, , ce qui est le résultatBarycentre de n points pondérés
On peut généraliser les propriétés à n points pondérés.
Définition
Définition
Soient
n points de l'espace. Soient 
n réels vérifiant 
.Le barycentre du système de points pondérés {
} est l'unique point G qui vérifie
Si 
, le barycentre n'existe pas. Connaître l'écriture formelle de la définition n'est d'aucun intérêt en soi. Il est en revanche fondamental de savoir écrire la définition du barycentre pour un système de points pondérés donné. Exemple
Soit G le barycentre du système de points pondérés {(A,1);(B,2);(C,3);(D,-4);(E,1)} (qui existe car
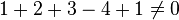), donc il vérifie l'égalité 
Propriétés
On suppose désormais que le barycentre G du système de points pondérés {
} existe, c'est-à-dire Invariance par multiplication par un réel non nul
Propriété
Soit k un réel non nul. Le barycentre de n points pondérés ne change pas si on multiplie tous les coefficients par k.
Égalité valable en tout point de l'espace
Propriété
Pour tout point M de l'esapce :
En pratique, lorsqu'on a besoin de cette relation, il faut procéder comme dans le cas à 2 ou 3 points : - Écrire la définition
- Introduire le point M avec la relation de Chasles
- Tout développer et mettre tous les termes en
du même côté de l'égalité
Coordonnées du barycentre
Propriété
On munit l'espace d'un repère
dans lequel A1(x1,y1,z1), A2(x2,y2,z2) ... An(xn,yn,zn)Les coordonnées de G dans
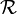sont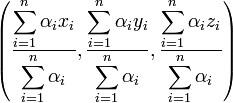 
Source : http://fr.wikiversity.org/