Barbidoux

Math 7-3.pdf

J'aurais plutôt dit deux car sin(π*x+π/3)=sin(-π*x+2*π/3) et sin(π*x-π/3)=sin(-π*x-2*π/3) … non ?

---------------- EXO 1 ----------------- ---------------- EXO 2 -----------------

le proton qui a une masse m est soumis à deux forces verticales lorsqu'il entre dans les armatures du condensateur. On néglige (q*E>> m*g) la force m*g due à la pesanteur devant celle provoqué q*E par le champ électrique vertical qui règne dans le condensateur. De cette force on déduit l'accélération verticale du proton ce qu permet d'obtenir par intégration la composante verticale de sa vitesse. On sait par ailleurs qu'il est animé d'une vitesse horizontale uniforme. On donc ainsi déterminé les deux composantes verticale vz(t) et horizontale vx(t)de sa vitesse à partir desquelles on peut décrire le mouvement horizontal x(t) et vertical z(t) du proton et obtenir l'équation de sa trajectoire z(x).

Qu'elle constante ??

2a—————————— un+2=5*un+1-6=5*(un-6)-6=5*un-36=4*un+un-36=un[4] 2b—————————— un+2=un[4] si n pair alors un+2=u2*k+2=u2*k[4]=u0[4]=2[4] ----------- si n impair alors un+2=u2*k+1=5*u2k-6=10[4]-2[4]=8[4]=0[4) 3a——————————

5) soit a un réel donné, déterminer l'ensemble Δa des points M tels que a soit racine de (E). Montrer que delta a est tangente à (C) ----------------------- Si a est racine de (E) alors a^2+a*b+c=0 et dans ce cas l'ensemble des Δa des points M{x,y} tels que le réel a soit racine de (E) est la droite d'équation a^2+a*x+y=0 ==> y=-a*x-a^2. Cette droite intercepte le graphe de ( C) en des points dont les abscisses sont les solutions du système d'équation : y=x^2/4 y=-a*x-a^2 ce système n'admettant qu'une solution (x=-a) on en déduit que Δa ne coupe le graphe de ( C) qu'en un seul point donc que ∆a est tangente à la courbe (C). ------------------------ 6) déterminer l'ensemble ∑ ' des points M tels que (E) admette deux racines réelles distinctes x' et x'' vérifiant -1 < x'<1<x". Préciser ∑' sur votre graphique. ------------------------ On cherche le lieu de M(b,c). On rappelle que dans l'équation x^2+b*x+c admet deux racines distinctes lorsque ∆=b^2-4*c>0 ==> c'est à dire lorsque M(x,y) est tel que y<x^2/4. Dans ce cas les racines sont respectivement : x'=(-b-√(b^2-4*c))/2 x"=(-b+√(b^2-4*c))/2 on en déduit que : -b=x'+x" ==> -b>0 ==> b<0 c'est à dire lorsque M(x,y) est tel que x<0 et -b-√(b^2-4*c)>-1 ==> -b+1>√(b^2-4*c) comme b<0 -b+1>0 et (-b+1)^2>(b^2-4*c) ==> -2*b+1>-4*c ==> 4*c>2*b-1 c'est à dire lorsque M(x,y) est tel que y>(2*x-1)/4 Conclusion l'ensemble ∑ ' des points M tels que (E) admette deux racines réelles distinctes x' et x'' vérifiant -1 < x'<1<x"est la zone du plan correspondant au abscisses négatives limitée par les portion de graphes de x=0, y=x^2/4 et y=(2*x-1)/4 respectant les conditions : x<0, y<x^2/4 et y>(2*x-1)/4.

4) Déterminer l'ensemble Δ 1 des points M tels que le réel 1 soit racine de (E). Construire Δ1 et montrer que Δ1 est tangente à la courbe (C). ----------------------- Si 1 est racine de (E) alors 1+b+c=0 et dans ce cas l'ensemble des Δ 1 des points M{x,y} tels que le réel 1 soit racine de (E) est la droite d'équation 1+x+y=0 ==> y=-x-1. Cette droite intercepte le graphe de ( C) en des points dont les abscisses sont les solutions du système d'équation : y=x^2/4 y=-x-1 ce système n'admettant qu'une solution on en déduit que Δ1 ne coupe le graphe de ( C) qu'en un seul point donc que ∆1est tangente à la courbe (C).

C'est par ce que les deux isomères sont représentés selon le même axe, il faut un peu d'imagination et faire tourner une des deux représentation de 180° pour obtenir 2 représentations symétriques par rapport à un plan...

molécules stéréoisomères images l'une de l'autre dans un miroir plan.

Salut Denis, sur mac pas de problème on enregistre et après on faut ce que l'on veut avec aperçu.... la seule chose gênante mais à laquelle personne ne peut rien c'est lorsque l'image jointe est de trop faible résolution ... ou de lecture difficile pour les gens qui n'ont plus des yeux aussi perçants qu'autrefois....

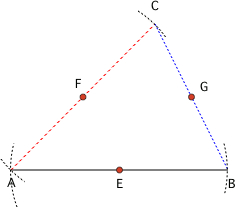
On trace d'abord trois points E,F et G non alignés. Ensuite on définit le segment AB, puis l'on place le point C et l'on joint C à B

A) On considère la formule topologique d'une molécule de phéromone qui appartient à un insecte nuisible pour les conifères: 1) Donner la formule semi-développée et la formule brute de cette molécule. ------------------ (CH3)C=CH-CH2-CH2-CHOH-CH3 C8H16O ==> M(C8H167O)=8*12+16+16=128 g/mol ------------------ 2) Cette molécule possède-t-elle des diastéréoisomères Z et E? ------------------ Non deux substituants identiques sur un des carbones de a double liaison ------------------ 3) Cette molécule possède un carbone asymétrique. Préciser lequel (étoile) et donner les représentations de Cram pour les molécules des deux énantiomères. Vous pouvez représenter le groupement ayant un grand nombre de carbone par sa formule brute. ------------------ 4) Pour attirer ces insectes nuisibles vers des forêts non exploitées, on les attire à l'aide de pièges renfermant une solution de la molécule de phéromone de 10-15 g.L-1 . Calculer la concentration molaire d'une telle solution. On donne les masses atomiques en g.mol-1 : M(H)=1; M(C)=12 et M(O)=16 ------------------ Cm=1*10^(-15)/128=7.81*10^(-18) mol/L ------------------ B) Les acides a-aminés possèdent une fonction acide carboxylique et, greffé sur le carbone voisin de cette fonction, un groupement amino (NH2) . 1) Donner la formule, la plus simple possible, de l'acide a-aminés qui ne possède pas de carbone asymétrique. Existe-t-il d'autres acides a-aminés qui ne possèdent pas de carbone asymétrique? Si oui, donner un exemple. ------------------ La quasi totalité des acides aminés possèdes un carbone asymétrique seule la glycine NH2-CH2-COOH ne possède pas de carbone asymétrique ------------------ 2) Donner la formule, la plus simple possible, de l'acide a-aminés qui possède un seul carbone asymétrique. Dessiner les représentations de Cram pour les molécules des deux énantiomères ------------------ NH2-CH(CH3)-COOH ------------------ C) On a représenté ci-dessous les formules topologiques dans l'espace (avec les conventions de la représentation de Cram) d'une molécule qui possède deux carbones asymétriques. 1) Traduire chaque formule topologique en représentation de Cram en rajoutant les symboles des atomes d'hydrogène et les liaisons vers les atomes d'hydrogène. 2) Vous devrez ensuite préciser, en justifiant votre affirmation, pour chacune des flèches, si elles relient des énantiomères ou des diastéréoisomères. ------------------

On peut (c'est le niveau de raisonnement le plus simple) compter le nombre des cartes (2 pour 1 étage 7 pour 2 étages 15 pour 3 étages etc…) ce qu'à proposé Denis. Pour aller plus loin on peut compter le nombre de cartes nécessaire à la constitution de chacun des étages du château et remarquer que tout ajout d'un étage supplémentaire nécessite trois cartes de plus que celles nécessaires pour constituer le l'étage précédent …. Ainsi il faut il faut 2 cartes pour réaliser le premier étage, 2+3=5 pour réaliser le second, 5+3 pour le troisième etc… Donc pour un château de 3 étage il faudra un nombre N de cartes égal à N=2+5+8=15 cartes et pour un château de 6 étages il faudra un nombre N de cartes égal à N=2+5+8+11+14+17=57 cartes Je pense qu'au niveau de la cinquième cela reste encore compréhensible. C'este ensuite que cela se gâte d'où mon intervention. Pour un nombre n d'étage il faudra faire la somme de n nombres en partant de 2, chaque nombre suivant étant égal au précédant auquel on ajoute 3 ce qui donnera N=2+5+8+11+14+…….. jusqu'à ce que l'on ait n nombres on voit comment faire mais cela ne donne toujours pas le nombre de cartes nécessaire. Ce nombre ne peut être obtenu qu'en utilisant des expressions que l'on ne voit que dans des classes de niveau beaucoup plus élevé. C'est la raison pour la quelle il me semble impossible (en cinquième) de donner le nombre N des cartes nécessaires pour réaliser un château d'un nombre n quelconque d'étages (et qui vaut N=(3*n^2+n)/2).

Et bien tu ne peux pas résoudre cet exercice en cinquième.... Tu peux éventuellement trouver combien de cartes il te faut pour faire un château de 6 étages mais un château d'un nombre quelconque n d'étages j'en serais fort surpris.

Tu es en cinquième ??? Cela m'étonnerais beaucoup .....

Le maths de cinquième ont bien changés .....

L'aire c'est A(x) et pour qu'elle soit inférieure ou égale à 9 cm^2 il faut que A(x)≤9 ==> 2x²-8x+15≤9 ==> 2x²-8x+15-9=≤0 ==> 2x²-8x+6 est une équation du second degré qui admet deux racines qui sont x=1 et x=3 et qui est du signe du coefficient de x^2 à l'extérieur de ses racines (voir ton cours) donc pour que A(x) ≤ 9 il faut que x appartienne à [1,3]

L'aire c'est A(x) et pour qu'elle soit égale à 9 cm^2 il faut que A(x)=9 ==> 2x²-8x+15=9 ==> 2x²-8x+15-9=0 ==> 2x²-8x+6=0 équation du second degré qui admet deux racines qui sont x=1 et x=3

Exercice 1 : ABCD est un rectangle tel que AB=3cm et BC=5cm. Les points M N P Q appartiennent aux côtés du rectangle et AM = BN = CP = DQ . On note "x" la longueur AM (en cm ) et "A" (x) l'aire de MNPQ (en cm²) 1) préciser l'ensemble de définition D de "A" ------------- x appartient à AB ==> x appartient à [0,3] ------------- 2) Démontrer que pour x appartient D : "A"(x)=2x²-8x+15 ------------- A(x)=Aire ABCD-Aire QAM-Aire MBN-Aire NCP-Aire PDM =15-2*x*(5-x)/2-2*x*(3-x)/2=2*x^2-8*x+15 ------------- 3) Peut on placer M de telle sorte que : a)MNPQ ait pour aire 9cm² ------------ il suffit de résoudre A(x)=9 ------------ b)MNPQ ait une aire strictement inférieure à 9cm² ------------ il suffit de résoudre A(x)-9≤0 ------------ 4) Dresser le tableau de variations de "A" sur D ------------ il suffit de résoudre A(x)=0 ------------ 5) Quelle est l'aire maximale de MNPQ ? et son aire minimale ? ------------ il suffit de trouver les valeurs maximales (x=0) et minimales de A(x) ({2,7} minimum du sommet de la parabole qui est le graphe de A(x)) ------------

B3------------ u0=-2 ≤-2^(2^0)=2 u1=-2-(-2)^2=-6 ≤-2^(2^1)=-4 u2=-6-(-6)^2=-42 ≤-2^(2^2)=-16 on suppose un=un-1-(un-1)^2≤ -2^(2^n) ---------- Par définition un+1=un-(un)^2 or un≤-2^(2^n) (un)^2≥ (2^(2^n))^2=2^(2^(n+1)) -------- un≤-2^(2^n) 2^(2^(n+1))≤(un)^2 --------- un+2^(2^(n+1)) ≤(un)^2-2^(2^n) un+1=un-(un)^2 ≤-2^(2^n)-2^(2^(n+1)) ≤ -2^(2^(n+1)) la relation étant héréditaire est vérifiée pour toute valeur de n et un≤ -2^(2^n) B4---------------- u0=1/2 u1=u0-u0^0 =u0*(1-u0)<u0=1/2 on suppose un<1/2 un+1=un*(1-un) <un<1/2 la relation étant héréditaire est vérifiée pour toute valeur de n ----------- u0=1/2 u1=u0-u0^0 =u0*(1-u0)>0 on suppose un>0 un+1=un*(1-un) comme un<1/2 et >0 ==> un+1>0 la relation étant héréditaire est vérifiée pour toute valeur de n Conclusion 0<un<1/2 B4b------------- suite bornée donc convergente un+1=un-un^2 ==> un+1-un=-un^2 <0 donc suite décroissante et la suite converge vers 0 sa borne inférieure B4c------------- ????? Je ne vois pas comment démonter rigoureusement que un<1/n ----------------------------------------- 31------------- f(x)=(5*x+1)/(x+5) définie sur [0 ∞[ f'(x)=5/(x+5)-(6*x+1)/(x+5)^5=24/(x+5)^2 >0 ==> f(x) est croissante sur son intervalle de définition 32------------- u0=3 u1=2 u2=11/7 u3=31/23 u4=89/73 un est décroissante et converge vers 1 33------------- Remarque : énoncé incorrect car on ne peut pas démonter par récurrence que 0≤ un+1≤un≤3. On peut par contre démontrer par récurrence que 0≤un≤3 puis que la suite est décroissante et que donc finalement 0≤un+1<un≤3 La suite un est croissante lorsque u0 appartient à [0,1[ et décroissante lorsque u0 appartient à ]1 ∞[ u0=3≥0 u1=2≥0 u2=11/7≥1 u3=31/23≥1 on suppose un≥0 un+1=(5*un+1)/(un+5)=(5*un+25-24)/(un+5) =5-24/(un+5) comme un≥0 ==> un+1≥0 la relation étant héréditaire est vérifiée pour toute valeur de n et un≥1 ----------- u1=2≤3 u2=11/7≤3 u3=31/23≤3 on suppose un≤3 un+1=(5*un+1)/(un+5) =(5*un+25-24)/(un+5) =5-24/(un+5) un≤3 ==> 24/(un+5) >4 et un+1 ≤3 la relation étant héréditaire est vérifiée pour toute valeur de n et un≤3 ------------ un+1-un= (5*un+1)/(un+5)-un=(1-un^2)/(un+5) comme un≥1 alors un+1-un<0 et la suite un est décroissante un est une suite bornée décroissante elle est donc convergente 34------------- vn=(un-1)/(un+1) vn+1=(un+1-1)/(un+1+1)=((5*un+1)/(un+5)-1)/((5*un+1)/(un+5)+1)=(4un-4)/(6*un+6)=(2/3)*(un-1)/(un+1)=(2/3)*vn La suite vn est une suite géométrique de raison 2/3 et de premier terme v0=2 ==> vn=2*(2/3)^n=(un-1)/(un+1) ==> un=((2/3)^n+1)/(1-(2/3)^n) Lorsque n->∞ alors (2/3)^n ->0 et lim un=1/1=1

exercice 1 Soient b et c deux réels données et (E) l'équation : x^2+ bx + c =0 d'inconnue réelle x. A chaque équation (E) on associe le plan M de coordonnées(b,c) dans un repère orthogonal du plan. 1) déterminer puis construire l'ensemble (C ) des points M tels que (E) admette une racine double. --------------------- cet ensemble ( C) est tel que b^2-4*c=0 ==> c=b^2/4. L'ensemble des points M{x,y} qui satisfait cette relation est la parabole d'expression y=x^2/4 puisque chacun des ses point d'abscisse x=b a pour ordonnée y=b^2/4. --------------------- 2) déterminer l'ensemble ∑ des points M tels que (E) admette deux solutions réelles distincts et confondus. --------------------- cet ensemble ∑ est tel que b^2-4*c>0 ==> c<b^2/4. L'ensemble des points M{x,y} qui satisfait cette relation se trouve en dessous de la parabole d'expression y=x^2/4 puisque chacun des ses point d'abscisse x=b a pour ordonnée b^2/4 tel que c<b^2/4 --------------------- 3) Discuter alors suivant la position de M dans ∑ le signe des racines de (E) ---------------------